


Školska knjižničarka nabavlja knjige za knjižnicu. Ukupno ima
kn i želi romane iz serijala o Harryju Potteru. Može li kupiti sve naslove?
Ako ne, koliko joj novca nedostaje?
Ako da, koliko će joj novca ostati?
| Naziv romana |
Cijena |
|---|---|
| Harry Potter i kamen mudraca | |
| Harry Potter i odaja tajni | |
| Harry Potter i zatočenik Azkabana | |
| Harry Potter i plameni pehar | |
| Harry Potter i Red feniksa | |
| Harry Potter i princ miješane krvi | |
| Harry Potter i darovi smrti |
Prethodni zadatak može se riješiti zbrajanjem cijena svih naslova i oduzimanjem od broja
Ukupna cijena svih naslova iznosi
Knjižničarka ima dovoljno novca za sve naslove te će joj ostati
Prisjeti se što već znaš o zbrajanju i oduzimanju prirodnih brojeva.
Na odgovarajuća mjesta postavi nazive brojeva u zbrajanju. (Pločice postavi preko brojeva.)
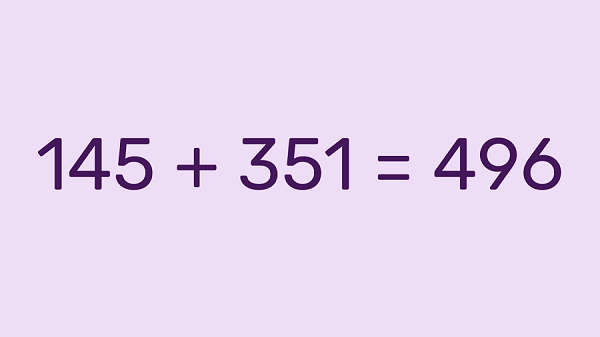
Brojeve koje zbrajamo zovemo pribrojnici, a rezultat zbrajanja zovemo zbroj (suma).
Na odgovarajuća mjesta na slici postavi nazive brojeva u oduzimanju.
(Pločice postavi preko brojeva.)
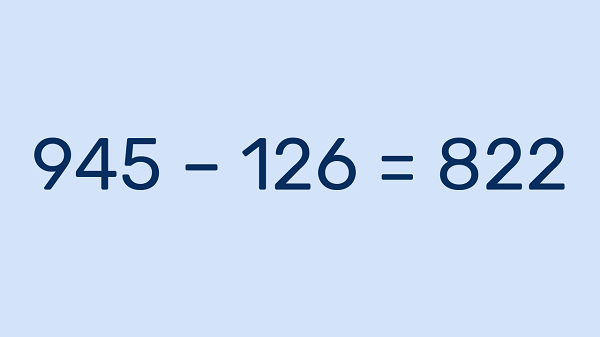
Broj koji umanjujemo nazivamo umanjenik. Broj kojim umanjujemo nazivamo umanjitelj. Rezultat oduzimanja nazivamo razlika (diferencija).
Zbroj dvaju prirodnih brojeva uvijek je prirodni broj.
Razlika dvaju prirodnih brojeva uvijek je prirodni broj.
Pomoć:
Je li rješenje zadatka - prirodan broj?
A rješenje zadatka
-
Ako je
onda je
Postupak:
Ako je umanjenik veći od umanjitelja, tada je razlika prirodan broj.
Ako je umanjenik jednak umanjitelju, razlika je jednaka broju
Zbroj dvaju prirodnih brojeva prirodni je broj.
Primjer 1.
Izračunaj pomoću različitih modela.
a) tablice mjesnih vrijednosti
b) koristeći se brojevnim pravcem
c) koristeći se modelom novca
d) pisanim zbrajanjem
a)
| T | S | D | J | |
|---|---|---|---|---|
| + | ||||
J više J je J. To je D i J.
D i D je D. Njima pribrajamo D pa je zbroj D. D je S i D.
S i S je S. S više S je S. S je T i S.
T više T je T.
b)
c)
d)
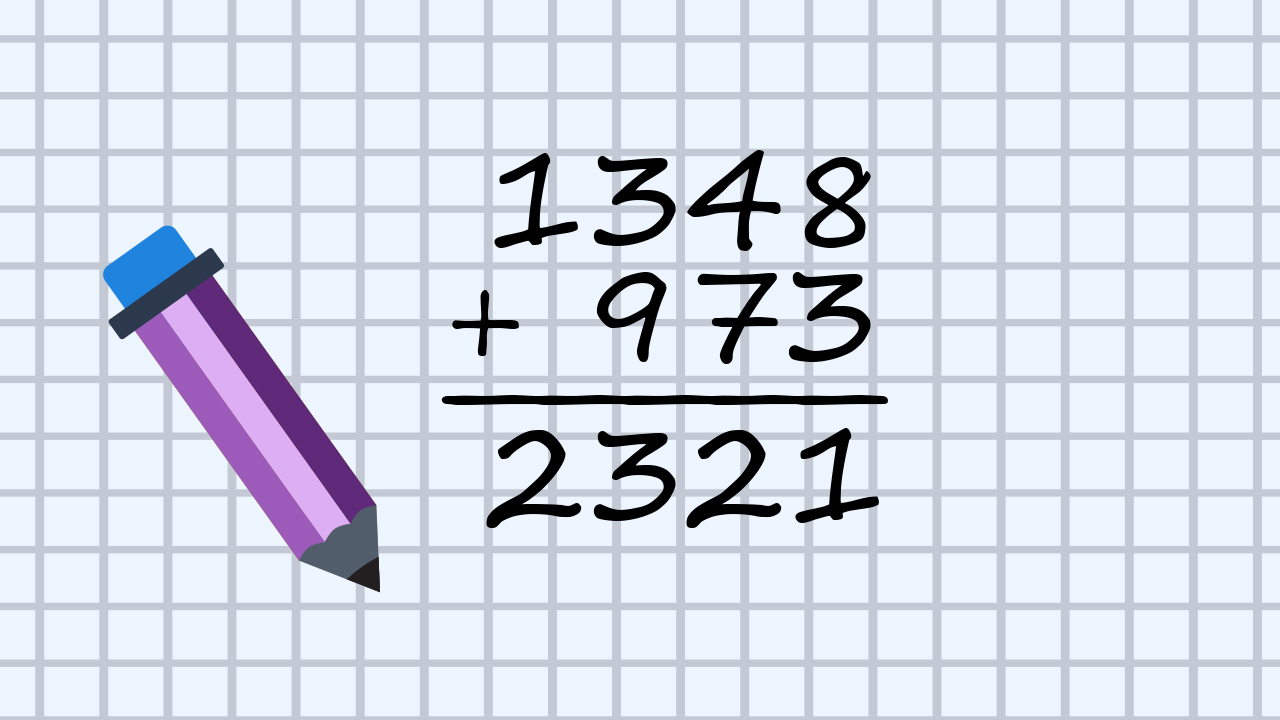
Koristeći se sljedećim apletom, uvježbaj pisano zbrajanje.
Tijekom prvih šest mjeseci od otvorenja muzej je prodao
ulaznice za umirovljenike. Ulaznica za odrasle prodano je za
više nego ulaznica za umirovljenike. Ulaznica za djecu prodano je za
više nego ulaznica za odrasle.
a) Koliko je prodano ulaznica za odrasle, a koliko za djecu?
b) Koliko je ukupno ulaznica prodano u prvih šest mjeseci od otvaranja?
a)
Prodana je ulaznica za odrasle.
Prodane su ulaznice za djecu.
b)
Ukupno je prodano
ulaznica.
Za školski sajam Petar je ispekao
kolačića, a Marita
a) Procijeni koliko su ukupno kolačića ispekli zaokružujući svaki broj na najbližu deseticu.
b) Izračunaj ukupan broj kolačića koje su ispekli.
a)
Ukupno su ispekli oko kolačića.
b)
Ukupno su ispekli
kolačića.
Neka je slastičarnica u subotu prodala kolača. U nedjelju nije bila otvorena. Koliko se kolača prodalo u toj slastičarnici tijekom vikenda?
U slastičarnici se tijekom vikenda prodalo
kolača.
Neutralni element za zbrajanje
Pribrojimo li nekom prirodnom broju nulu, broj se neće promijeniti.
Kažemo da je neutralni element za zbrajanje prirodnih brojeva.
Istražimo
Koristeći se apletom, istraži ovisnost zbroja o redoslijedu pribrojnika.
Što primjećuješ?
Komutativnost zbrajanja
Ako pribrojnici zamijene mjesta, zbroj se neće promijeniti. To se svojstvo naziva komutativnost zbrajanja.
Istražimo
Koristeći se apletom, istraži ovisnost zbroja o načinu grupiranja pribrojnika.
Asocijativnost zbrajanja
Grupiramo li pribrojnike na različite načine, zbroj će ostati isti. To svojstvo nazivamo asocijativnost zbrajanja.
Izračunaj napamet. Objasni postupak rješavanja.
a)
b)
a)
b)
Primjenom svojstava komutativnosti i asocijativnosti združe se pribrojnici čiji je zbroj višekratnik dekadske jedinice, a zatim se međuzbrojevi zbroje.
Učiteljica je zapisala broj sudionika škole u natjecanju Klokan bez granica po razredima.
| Razred | Broj sudionika |
|---|---|
| Prvi | |
| Drugi | |
| Treći | |
| Četvrti | |
| Peti | |
| Šesti | |
| Sedmi | |
| Osmi |
Pomoć:
Potraži parove brojeva koje je jednostavno zbrojiti.
Postupak:
Primjer 2.
Izračunaj pomoću različitih modela.
a) tablice mjesnih vrijednosti
b) koristeći se brojevnim pravcem
c) koristeći se modelom novca
d) pisanim oduzimanjem
a)
| T | S | D | J | |
|---|---|---|---|---|
| - | ||||
J manje J je J.
U stupcu desetica ostale su D ( D D D).
D manje D je D.
S manje S je S.
T manje T je T.
b)
c)
d)

Koristeći se sljedećim apletom, uvježbaj pisano oduzimanje.
Primjer 3.
Tvoja škola za svoje učenike naručuje privjeske za ključeve s logom škole. Školu pohađa učenika. Ravnateljica je pri naručivanju zaokružila broj privjesaka na najbližu stoticu. Hoće li biti dovoljno privjesaka za sve učenike? Objasni svoj odgovor.
Broj
zaokružen na najbližu stoticu je broj
Neće biti dovoljno privjesaka za svakog učenika. Nedostajat će
privjeska.
Slavni teoretski fizičar Stephen Hawking rodio se 8. siječnja 1942. godine, a preminuo 14. ožujka 2019. godine.
Albert Einstein, jedan od najpoznatijih znanstvenika svih vremena, teorijski fizičar koji je formulirao teoriju relativnosti, rodio se 14. ožujka 1879. godine.
Galilelo Galilei, talijanski fizičar i astronom koji je izumio teleskop i prvi ga usmjerio prema nebu, preminuo je 8. siječnja 1642. godine.
Tablica prikazuje proizvodnju maslina u tonama u Republici Hrvatskoj.
| 2016. | 2017. | 2018. |
|---|---|---|
|
|
|
|
(Podatci preuzeti s mrežnih stranica Državnog zavoda za statistiku.)
a) Kakav je trend proizvodnje maslina u Republici Hrvatskoj? (Raste li proizvodnja ili pada?)
b) Za koliko se razlikuje proizvodnja maslina u 2018. u odnosu na 2016. godinu?
c) Za koliko se razlikuje proizvodnja maslina u 2018. u odnosu na 2017. godinu?
a) Na temelju prikazanih podataka možemo zaključiti da proizvodnja maslina u Republici Hrvatskoj opada.
b)
Proizvodnja maslina u 2018. godini u odnosu na 2016. smanjila se za
tona.
c)
Proizvodnja maslina u 2018. godini u odnosu na 2017. smanjila se za
tona.
Ako želiš, dodatno uvježbaj zbrajanje i oduzimanje rješavajući križaljke.
Klikom odaberi zadatak koji želiš riješiti. Nakon što točno riješiš zadatak, rješenje će se upisati u križaljku.