Matematika 3 - 6.2 Rješavanje trigonometrijskih jednadžbi pomoću grafa funkcije

Ponovimo

Neka su dane elementarne trigonometrijske jednadžbe oblika $\sin x = a$ i $\cos x = a,$ gdje je konstanta $a$ dani realni broj.

Prisjetite se osnovnih svojstva trigonometrijskih funkcija.

Trigonometrijske su funkcije

funkcije.

Temeljni je period funkcija sinus i kosinus

,

a funkcija tangens i kotangens

.

Stoga se njihove vrijednosti

ponavljaju

pa se i graf duljine temeljnog perioda funkcije (jedan val sinusoide) ponavlja

mnogo

puta.

null

Na intervalu širine temeljnog perioda, grafovi funkcija sinus i kosinus (jedan val) imaju jedan brijeg i jedan dol.
Funkcija sinus ima

nultočke,

dok funkcija kosinus ima

nultočke,

što znači da je to ukupan broj rješenja elementarnih trigonometrijskih jednadžbi

\sin x = 0

i

\cos x = 0

na intervalu

[0, 2 π] .

Funkcija sinus ima

maksimum

i

minimum.

Funkcija kosinus ima

maksimuma

i

minimum.

To je ujedno i broj rješenja elementarih trigonometrijskih jednadžbi

\sin x = \pm A

i

\cos x = \pm A

na intervalu

[0, 2 π]

, gdje je

A

amplituda pripadajuće trigonometrijske funkcije.

null

Broj rješenja trigonometrijske jednadžbe oblika $A \sin x = a, A \cos x = a, x \in R$ ovisi o $a$ .

Trigonometrijska jednadžba ima beskonačno mnogo rješenja ako je
Trigonometrijska jednadžba nema rješenja ako je

null

Dana je sinusoida oblika $y = A \sin (b x + c) .$ Povežite oznake s pripadajućim pojmovima.

$A$
$b$
$c$
$d$
$\frac{2 π}{\|b\|}$
$- \frac{c}{b}$

null

Prisjetimo se kako zavisna varijabla $y$ ovisi o nezavisnoj varijabli $x,$ odnosno pogledajmo kako na grafu "pročitati" rješenje presjeka pravca paralelnog s osi apscisa i sinusoide.

Dobro definirana trigonometrijska jednadžba ima

rješenja.

To je posljedica

trigonometrijskh

funkcija.

null

Trigonometrijska jednadžba $\sin x = a$ na intervalu $[0, 2 π⟩$ ima najviše dva rješenja.

Da

Ne

null

Trigonometrijska jednadžba Asin(bx + c) + d = 0

Kako bismo olakšali traženje rješenja trigonometrijske jednadžbe $A \sin (b x + c) + d = 0,$ sredimo je.

$A \sin (b x + c) + d = 0 \Rightarrow \sin (b x + c) = - \frac{d}{A} .$

Možemo uvesti supstituciju $b x + c = t$ pa se početna jednadžba svodi na elementarnu trigonometrijsku jednadžbu oblika $\sin t = a,$ gdje je $t = b x + c, a = - \frac{d}{A} .$

Elementarnu sinusoidu lako nacrtamo i odredimo prva dva pozitivna sjecišta s pravcem $y = a .$

Primjer 1.

Grafičkom metodom riješimo jednadžbu: $2 \sin (2 x - \frac{π}{6}) - 1 = 0 .$

Sređena jednadžba jest: $\sin t = \frac{1}{2}, t = 2 x - \frac{π}{6} .$ Nacrtajmo sinusoidu $y = \sin t$ i pravac $y = \frac{1}{2} .$

Prethodna nam je animacija dala rješenja.

Nama su zanimljiva sjecišta unutar intervala $[0, 2 π⟩ .$

Jedan brijeg/dol sinusoide pravac siječe u dvije točke: $t_{1} = \frac{π}{6}, t_{2} = \frac{5 π}{6} .$

Dva rješenja imamo. Zbog periodičnosti funkcije sinus pišemo: $t_{1} = \frac{π}{6} + 2 k π, t_{2} = \frac{5 π}{6} + 2 k π, k \in Z .$

Uvrstimo li dobivena rješenja u početnu supstituciju, dobijemo: $2 x - \frac{π}{6} = \frac{π}{6} + 2 k π \Rightarrow 2 x = \frac{π}{3} + 2 k π .$ Dijeljenjem cijele jednadžbe s 2 konačno imamo jedan skup rješenja: $x = \frac{π}{6} + k π, k \in Z .$

Analogno za drugi skup rješenja dobijemo: $x = \frac{π}{2} + k π, k \in Z .$

Zadatak 1.

Riješite jednadžbu: $3 \sin (\frac{x}{3} + \frac{π}{3}) + 3 = 0 .$

Ovdje imamo specijalni slučaj u kojem sinusoida siječe pravac samo u jednoj točki na intervalu temeljnog perioda. To je točka minimuma funkcije.

$\frac{x}{3} + \frac{2 π}{3} = \frac{3 π}{2} + 2 k π \Rightarrow x = \frac{5 π}{2} + 6 k π, k \in Z$

Isto vrijedi kada imamo točku maksimuma $(\sin x = 1) .$

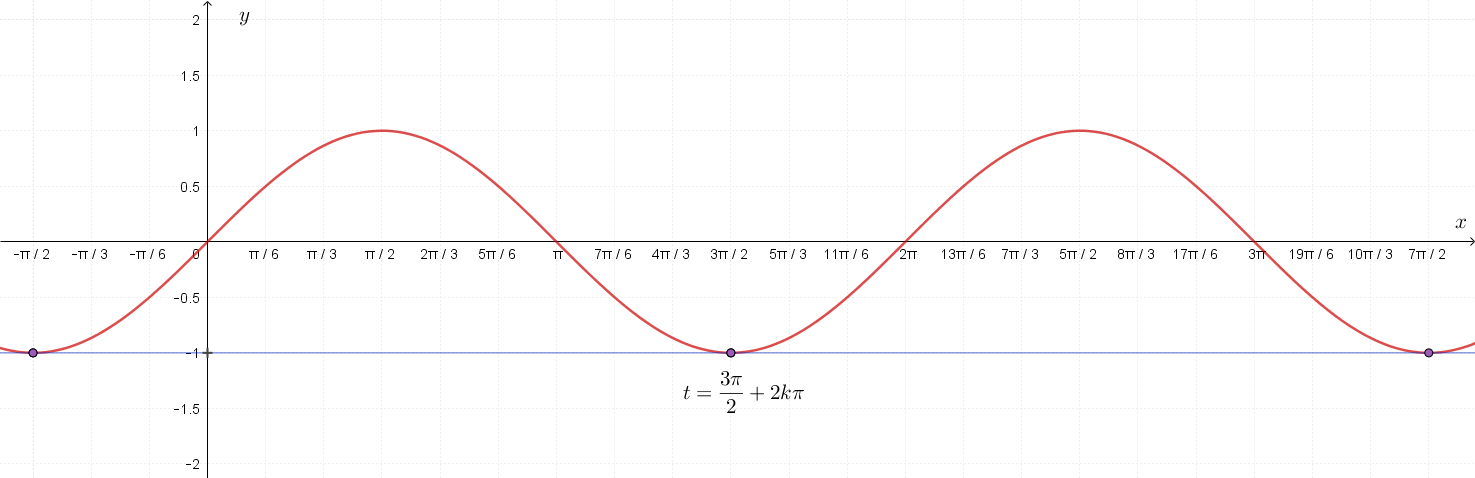
Početno grafičko rješenje zadatka 1. — Grafički prikaz početne jednadžbe

Ne možemo uvijek rješenja dobiti iz tablica. Poslužit ćemo se sljedećim interaktivnim prikazom (pomočući plavi trokutić) kako bismo grafičkom metodom dobili što točnije rješenje presjeka pravca i elementarne sinusoide.

Primjer 2.

Riješimo jednadžbu: $\frac{4}{3} \sin (3 x - \frac{π}{8}) - \frac{1}{3} = 0 .$

Zapišimo jednadžbu u obliku: $\sin t = \frac{1}{4}, t = 3 x - \frac{π}{8} .$

Prva dva presjeka grafa funkcije sinus s pravcem $y = \frac{1}{4}$ desno od nule jest u točkama $(0.2527, \frac{1}{4}) i (2.8889, \frac{1}{4}) .$
Dakle, $3 x - \frac{π}{8} = 0.2527 + 2 k π$ i $3 x - \frac{π}{8} = 2.8889 + 2 k π \Rightarrow$

$3 x = 0.6454 + 2 k π$ ili $3 x = 3.2816 + 2 k π .$

Sva su rješenja: $x_{1} = 0.2151 + \frac{2 k π}{3}, x_{2} = 1.0939 + \frac{2 k π}{3}, k \in Z .$

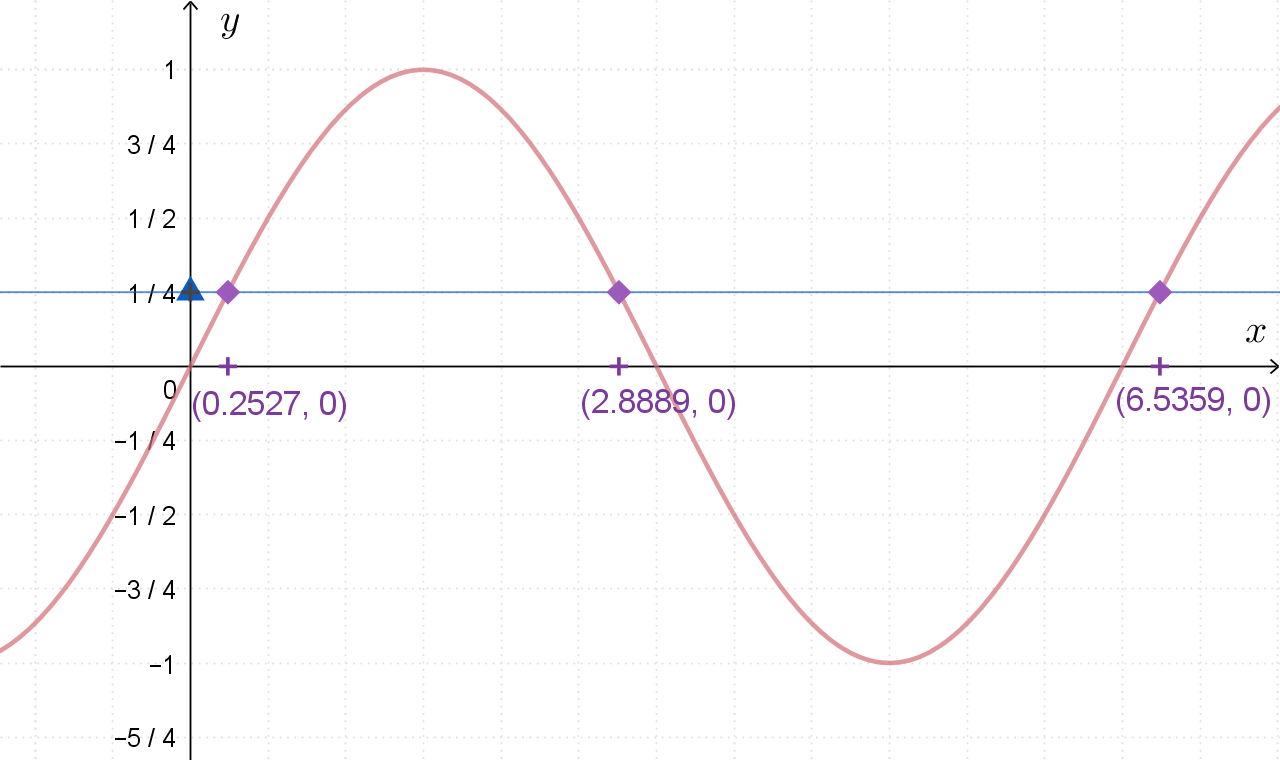
Grafički dio rješavanja jednadžbe. — Grafički prikaz početne jednadžbe

Zadatak 2.

Riješite jednadžbu: $\sin (x + 2) + 1 = 4 \sin (x + 2) .$

$x_{1} = - 1.6602 + 2 k π, x_{2} = 0.8018 + 2 k π, k \in Z$

Grafički dio rješavanja jednadžbe zadatka 2. — Grafički prikaz početne jednadžbe

Trigonometrijska jednadžba Acos(bx + c) + d = 0

Analogno kao i kod jednadžbi sa sinusom, rješavamo i trigonometrijske jednadžbe s kosinusom. Pojednostavnjena jednadžba jest: $\cos t = - \frac{d}{A}, t = b x + c .$ Promatramo presjek grafa funkcije kosinus s pravcem $y = - \frac{d}{A}$ i odredimo dva suprotna rješenja najbliža nuli.

Primjer 3.

Riješimo jednadžbu: $2 \cos (2 x - \frac{π}{3}) + \sqrt{3} = 0 .$

Jednadžbu svedemo na oblik: $\cos (2 x - \frac{π}{3}) = - \frac{\sqrt{3}}{2} .$

Apscise točaka presjeka dviju krivulja najbliže nuli jesu $\pm \frac{5 π}{6} .$

$2 x - \frac{π}{3} = \frac{5 π}{6} + 2 k π \Rightarrow x_{1} = \frac{7 π}{12} + k π, k \in Z$

$2 x - \frac{π}{3} = - \frac{5 π}{6} + 2 k π \Rightarrow x_{1} = - \frac{π}{4} + k π, k \in Z$

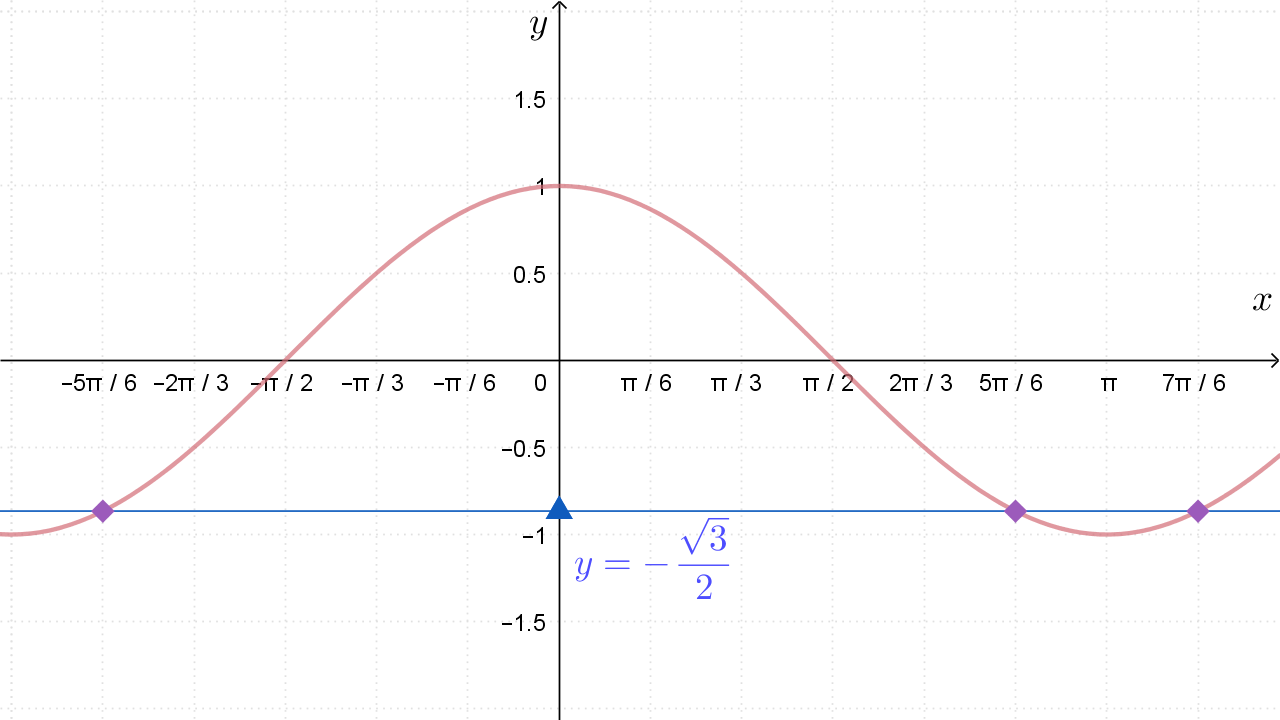
Početno grafičko rješenje primjera 3. — Grafički prikaz početne jednadžbe

Zadatak 3.

Riješite jednadžbu: $\sqrt{8} \cos (0.25 x + \frac{π}{12}) - 2 = 0 .$

$x_{1} = \frac{2 π}{3} + 8 k π, x_{2} = - \frac{4 π}{3} + 8 k π, k \in Z$

Grafički dio rješavanja jednadžbe zadatka 3. — Grafički prikaz početne jednadžbe

Kao pomoć pri rješavanju trigonometrijskih jednadžbi s funkcijom kosinus iskoristite sljedeći interaktivni graf na kojem pomičete pravac pomoću plavog trokutića kako biste dobili željeni presjek.
Riješite prethodni Primjer 3. i Zadatak 3. pomoću ove interakcije.

Zadatak 4.

Riješite jednadžbu: $15 - 18 \cos (\frac{π}{8} - \frac{x}{4}) = 0 .$

Zbog parnosti funkcije kosinus možemo pisati: $\cos (\frac{x}{4} - \frac{π}{8}) = \frac{5}{6} .$

$x_{1} = - 0.77 + 8 k π$ i $x_{2} = 3.91 + 8 k π, k \in Z$

Zadatak 5.

Za kraj riješite jedan problemski zadatak. Interakcijom u nastavku je prikazana promjena razine vode u ribnjaku tijekom jedne godine (365 dana), počevši s najtoplijim danom u godini. Odredite nakon koliko će dana od najtoplijeg dana u godini razina vode u ribnjaku pasti na $30 cm$ . Koliko je dana/mjeseci u godini razina vode ispod $30 cm ?$

Nakon $152$ dana razina vode bit će na $30 cm$ . Manje od $30 cm$ bit će od $152 .$ do $213 .$ dana, što iznosi $61$ dan, odnosno $2$ mjeseca.

...i na kraju

Naučili smo tražiti rješenja osnovnih trigonometrijskih funkcija pomoću brojevne kružnice i sinusoide. Vidjeli smo da nam od velike pomoći može biti i tehnologija, konkretno dinamični program geometrije (geogebra). No, što ako pri ruci nemamo digitalne alate? Ipak ćemo ove jednadžbe trebati naučiti rješavati i klasičnim putem, što vas čeka u sljedećim jedinicama.

Na početku...

Ponovimo

Trigonometrijska jednadžba Asin(bx + c) + d = 0

Primjer 1.

Zadatak 1.

Primjer 2.

Zadatak 2.

Trigonometrijska jednadžba Acos(bx + c) + d = 0

Primjer 3.

Zadatak 3.

Zadatak 4.

Zadatak 5.

...i na kraju