3.4 Sljedeća jedinica Čimbenici koji utječu na pomak kemijske ravnoteže
3.3

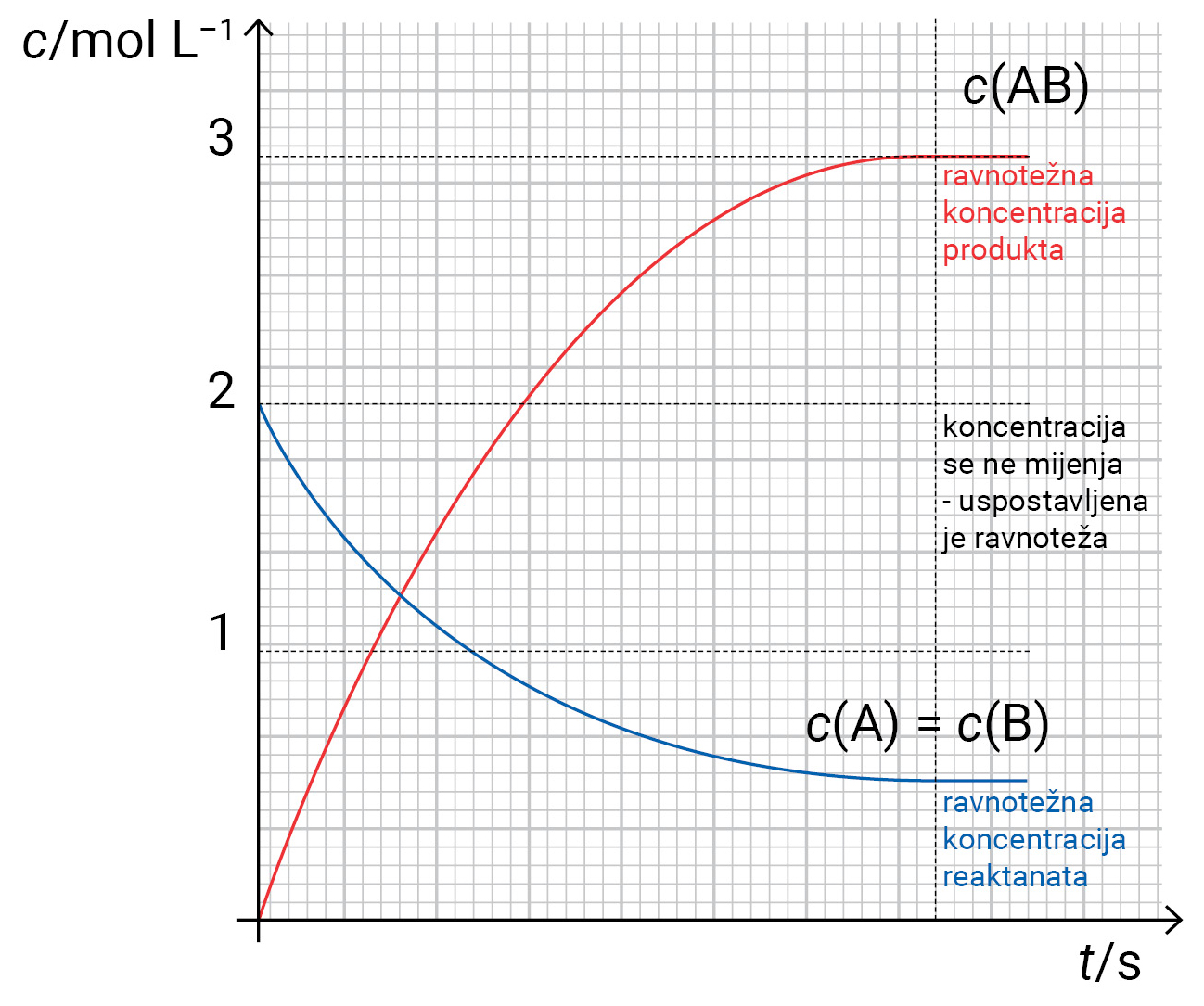
Ravnoteža kemijskih reakcija

Moći ću:
  • objasniti pojam ravnotežnog stanja kemijskoga sustava
  • napisati izraz za empirijsku konstantu ravnoteže kemijskoga sustava

Uvod

Iz izjednačene jednadžbe kemijske reakcije mogli bismo zaključiti da su svi reaktanti reagirali uz nastajanje odgovarajućih produkata.

Međutim, kod velikog broja kemijskih reakcija dolazi do uspostavljanja kemijske ravnoteže.

To se događa nakon nekog vremenskog razdoblja, određenog kinetikom kemijske reakcije,

Izjednačavaju se brzine (v) polazne i povratne reakcije.

Koncentracije (c) reaktanata i produkata se ne mijenjaju, ako se ne promjene uvjeti reakcije.

Poznavanje zakonitosti, koje se odnose na sustave u ravnoteži i uvjete kojima možemo mijenjati ravnotežno stanje, omogućava:

  • veće  (>) iskorištenje reaktanata,
  • uštede energije
  • smanjenje otpada.

 

Uvod

Iz izjednačene jednadžbe kemijske reakcije mogli bismo zaključiti da su svi reaktanti reagirali uz nastajanje odgovarajućih produkata. Međutim, kod velikog broja kemijskih reakcija, nakon nekog vremenskog razdoblja, određenog kinetikom kemijske reakcije, dolazi do uspostavljanja kemijske ravnoteže. Izjednačavaju se brzine polazne i povratne reakcije. Koncentracije reaktanata i produkata se ne mijenjaju, ako se ne promjene uvjeti reakcije.

Poznavanje zakonitosti koje se odnose na sustave u ravnoteži i uvjeta kojima možemo mijenjati ravnotežno stanje omogućava veće iskorištenje reaktanata, uštede energije i smanjenje otpada.

Slika prikazuje dvije siluete, muška i ženska. Siluete su ispunjene simbolom ravnoteže, malim vagama u ravoteži obojenim plavom, žutom, crvenom i zelenom bojom.

Istraži - Istraži

Natrij-kalijeva crpka jedan je od primjera kako ljudsko tijelo održava ravnotežu neophodnu za metaboličke procese.

Pri rješavanju stehiometrijskih zadataka najčešće pretpostavljamo da reakcija napreduje dok se ne potroši jedan od reaktanata.

Takve su reakcije nepovratne ili ireverzibilne.

Neke reakcije mogu se odvijati u oba smjera.

Stoga, razlikujemo:

1. napredne ili polazne reakcije
2. povratne ili reverzibilne reakcije.

Općenito, povratnu reakciju možemo prikazati kao:

\ce{A2(g) + B2(g)<=> 2AB(g)}

Ako se smjesa reaktanata A2 (g) i B2 (g) stavi u reakcijsku posudu doći će do stvaranja produkta reakcije AB.

Napredovanjem polazne reakcije smanjuju se koncentracije (c) reaktanata A i B.

Stoga, smanjuje se i brzina polazne reakcije.

Do povratne reakcije može doći tek kada u reakcijskoj smjesi nastane nešto produkta AB.

Brzina povratne reakcije je na početku mala jer je mala i koncentracija (c) produkta AB.

Prema tome, tijekom vremena brzina polazne reakcije se smanjuje.

Brzina povratne reakcije raste sve dok se ne izjednače.

U tom se trenutku uspostavlja dinamička kemijska ravnoteža.

U stanju ravnoteže, koncentracije svih tvari u reakciji su stalne.

U ravnoteži ne prestaju niti polazne niti povratne reakcije.

Njihove brzine su izjednačene.

To je razlog da se koncentracije tvari u ravnoteži ne mijenjaju.

Pri rješavanju stehiometrijskih zadataka najčešće pretpostavljamo da reakcija napreduje dok se ne potroši jedan od reaktanata. Takve su reakcije nepovratne ili ireverzibilne.

Međutim, neke reakcije se mogu odvijati u oba smjera, pa razlikujemo napredne (polazne) i povratne reakcije ili reverzibilne reakcije.

Općenito povratnu reakciju možemo prikazati kao:

\ce{A2(g) + B2(g)<=> 2AB(g)}

Ako se smjesa reaktanata A2(g) i B2(g) stavi u reakcijsku posudu doći će do stvaranja produkta reakcije AB.

Budući da se napredovanjem polazne reakcije smanjuju koncentracije reaktanata A i B, smanjuje se i brzina polazne reakcije.

Do povratne reakcije može doći tek kada u reakcijskoj smjesi nastane nešto produkta AB. Brzina povratne reakcije je na početku mala jer je mala i koncentracija produkta AB. Prema tome tijekom vremena brzina polazne reakcije se smanjuje, a brzina povratne reakcije raste sve dok se ne izjednače. U tom se trenutku uspostavlja dinamička kemijska ravnoteža.

U stanju ravnoteže, koncentracije svih tvari u reakciji su stalne. U ravnoteži ne prestaju niti polazne niti povratne reakcije već su njihove brzine izjednačene pa je to razlog da se koncentracije tvari u ravnoteži ne mijenjaju.

Konstanta kemijske ravnoteže

Pretpostavimo da je mehanizam i polazne i povratne reakcije jednostavan, da se reakcije odvijaju u jednom koraku.

Za reakciju:

\ce{A2(g) + B2(g) <=> 2AB(g)}

vrijedi zakon brzine:

v_{1} = k_{1}\cdot [\ce{A2}]\cdot [\ce{B2}]

v_{2} = k_{2}\cdot [\ce{AB}]^{2}

U stanju dinamičke ravnoteže brzine (v) su izjednačene (=):

v_{1} = v_{2}

k_{1}\cdot [\ce{A2}]\cdot [\ce{B2}] = k_{2}\cdot [\ce{AB}]^{2}

\dfrac{k_1}{k_2} = \dfrac{[\ce{AB}]^{2}}{[\ce{A2}]\cdot [\ce{B2}]}

Omjer konstante brzine polazne i konstante brzine povratne reakcije nova je konstanta, K. Naziva se konstanta kemijske ravnoteže.

K = \dfrac{k_1}{k_2} = \dfrac{[\ce{AB}]^{2}}{[\ce{A2}]\cdot [\ce{B2}]}

Budući da konstanta kemijske ravnoteže predstavlja omjer množinskih koncentracija (c) naziva se i koncentracijska konstanta kemijske ravnoteže. Označava se Kc.

Njena brojčana vrijednost ovisi isključivo o temperaturi.

Mjerna jedinica konstante ravnoteže  (Kc) različita je za različite reakcije, ovisno o stehiometrijskim koeficijentima reaktanata i produkata reakcije.

Kemijska se ravnoteža može uspostaviti samo u zatvorenom sustavu, bez obzira na polazno stanje sustava.
Određuje se eksperimentalnim putem.

Općenito za bilo koju ravnotežnu reakciju prikazanu izrazom:

\ce{aA + bB <=> cC + dD}

izraz za koncentracijsku konstantu ravnoteže (Kc) je:

K_{\textrm{c}} = \dfrac{[\ce{C}]^{\textrm{c}}\cdot \ce{D}]^{\textrm{d}}}{[\ce{A}]^{\textrm{a}}\cdot \ce{B}]^{\textrm{b}}}

Koncentracijska konstanta ravnoteže, Kc, jednaka (=) je omjeru umnoška množinskih koncentracija (c) produkata i umnoška množinskih koncentracija (c) reaktanata.

Pri tome, svaka množinska koncentracija (c) je potencirana apsolutnom vrijednošću vlastitog stehiometrijskog koeficijenta.

Konstanta ravnoteže (Kc) ima stalnu vrijednost pri određenoj temperaturi.

Taj izraz poznat je kao zakon o djelovanju masa ili Guldberg – Waageov zakon.

Vrijednosti konstante ravnoteže

Ako je brojčana vrijednost konstante ravnoteže, Kc:

  • manja (<) od 0,01;
    onda je ravnoteža reakcije pomaknuta na stranu reaktanata. Tada u ravnotežnoj reakcijskoj smjesi ima puno neizreagiranih reaktanata i neznatno produkata
  • između 0,01 i 100;
    tada su u ravnotežnoj smjesi prisutni i reaktanti i produkti u značajnoj količini
  • veća (>) od 100,
    onda je ravnoteža reakcije pomaknuta na stranu produkata. Tada u ravnotežnoj reakcijskoj smjesi ima malo neizreagiranih reaktanata i puno nastalih produkata.

Za reakciju u kojoj su reaktanti i produkti plinovi, u konstante ravnoteže iskazujemo parcijalnim tlakovima plinovitih sudionika reakcije pa tlačna konstanta ravnoteže, Kp, za navedeni sustav glasi:

\ce{N2O4(g) <=> 2NO2(g)}

K_{\textrm{p}} = \dfrac{p^{2}(\ce{NO2})}{p(\ce{N2O4})}

Tlačna konstanta ravnoteže,  Kp, povezana je s koncentracijskom konstantom ravnoteže, Kc, izrazom:

K_{\textrm{p}} = K_{\textrm{c}}\cdot (RT)^{\Delta n}

gdje je:

\Delta n – razlika između sume stehiometrijskih koeficijenata (ν) produkata i sume stehiometrijskih (ν) koeficijenata reaktanata

R = \pu{8,314e3 Pa dm3 mol-1 K-1}

Konstanta kemijske ravnoteže

Pretpostavimo da je mehanizam i polazne i povratne reakcije jednostavan, da se reakcije odvijaju u jednom koraku. Za reakciju:

\ce{A2(g) + B2(g) <=> 2AB(g)}

vrijedi zakon brzine:

v_{1} = k_{1}\cdot [\ce{A2}]\cdot [\ce{B2}]

v_{2} = k_{2}\cdot [\ce{AB}]^{2}

U stanju dinamičke ravnoteže brzine su izjednačene:

v_{1} = v_{2}

k_{1}\cdot [\ce{A2}]\cdot [\ce{B2}] = k_{2}\cdot [\ce{AB}]^{2}

\dfrac{k_1}{k_2} = \dfrac{[\ce{AB}]^{2}}{[\ce{A2}]\cdot [\ce{B2}]}

Omjer konstante brzine polazne i konstante brzine povratne reakcije nova je konstanta, K, a naziva se konstanta kemijske ravnoteže.

K = \dfrac{k_1}{k_2} = \dfrac{[\ce{AB}]^{2}}{[\ce{A2}]\cdot [\ce{B2}]}

Budući da konstanta kemijske ravnoteže predstavlja omjer množinskih koncentracija naziva se i koncentracijska konstanta kemijske ravnoteže, Kc, a njena brojčana vrijednost ovisi isključivo o temperaturi.

Mjerna jedinica konstante ravnoteže različita je za različite reakcije, a ovisi o stehiometrijskim koeficijentima reaktanata i produkata reakcije.

Kemijska se ravnoteža može uspostaviti samo u zatvorenom sustavu, bez obzira na polazno stanje sustava, a određuje se eksperimentalnim putem.

Općenito za bilo koju ravnotežnu reakciju prikazanu izrazom:

\ce{aA + bB <=> cC + dD}

izraz za koncentracijsku konstantu ravnoteže je:

K_{\textrm{c}} = \dfrac{[\ce{C}]^{\textrm{c}}\cdot \ce{D}]^{\textrm{d}}}{[\ce{A}]^{\textrm{a}}\cdot \ce{B}]^{\textrm{b}}}

 

Koncentracijska konstanta ravnoteže, Kc, jednaka je omjeru umnoška množinskih koncentracija produkata i umnoška množinskih koncentracija reaktanata gdje je svaka množinska koncentracija potencirana apsolutnom vrijednošću vlastitog stehiometrijskog koeficijenta. Konstanta ravnoteže ima stalnu vrijednost pri određenoj temperaturi.Taj izraz poznat je kao zakon o djelovanju masa ili Guldberg – Waageov zakon.

Vrijednosti konstante ravnoteže

Ako je brojčana vrijednost konstante ravnoteže , Kc:

  • manja od 0,01;  onda je ravnoteža reakcije pomaknuta na stranu reaktanata. Tada u ravnotežnoj reakcijskoj smjesi ima puno neizreagiranih reaktanata i neznatno produkata
  • između 0,01 i 100;  tada su u ravnotežnoj smjesi prisutni i reaktanti i produkti u značajnoj količini.
  • veća od 100, onda je ravnoteža reakcije pomaknuta na stranu produkata. Tada u ravnotežnoj reakcijskoj smjesi ima malo neizreagiranih reaktanata i puno nastalih produkata.

 

Za reakciju u kojoj su reaktanti i produkti plinovi, konstante ravnoteže iskazujemo parcijalnim tlakovima plinovitih sudionika reakcije. Tlačna konstanta ravnoteže, Kp, za navedeni sustav glasi:

\ce{N2O4(g) <=> 2NO2(g)}

K_{\textrm{p}} = \dfrac{p^{2}(\ce{NO2})}{p(\ce{N2O4})}

 

Tlačna konstanta ravnoteže,  Kp, povezana je s koncentracijskom konstantom ravnoteže, Kc, izrazom:

K_{\textrm{p}} = K_{\textrm{c}}\cdot (RT)^{\Delta n}

gdje je:

\Delta n – razlika između sume stehiometrijskih koeficijenata produkata i sume stehiometrijskih koeficijenata reaktanata
R = \pu{8,314e3 Pa dm3 mol-1 K-1}

Iz navedenih konstanti ravnoteže, (Kc)  napišite odgovarajuće jednadžbe kemijskih reakcija:

a) K_{\textrm{c}} = \dfrac{[\ce{NH3}]^{2}}{[\ce{H2}]^{2}\cdot [\ce{N2}]}

b) K_{\textrm{c}} = \dfrac{[\ce{SO3}]^{2}}{[\ce{SO2}]^{2}\cdot [\ce{O2}]}

c) K_{\textrm{c}} = \dfrac{[\ce{CO}]\cdot [\ce{Br2}]}{[\ce{COBr2}]}

d) K_{\textrm{c}} = \dfrac{[\ce{CO}]\cdot [H2]^{3}}{[\ce{CH4}]\cdot [\ce{H2O}]}

Jednadžbe napišite uz pomoć alata za Pisanje kemijskih jednadžbi na webu.

Odgovor:

a) \ce{3H2(g) + N2(g) 2NH3(g)}
 
b) \ce{2SO2(g) + O2(g) 2SO3(g)}
 
c) \ce{COBr2(g) CO(g) + Br2(g)}
 
d) \ce{CH4(g) + H2O(g) CO(g) + 3H2}

Iz navedenih konstanti ravnoteže, napišite odgovarajuće jednadžbe kemijskih reakcija:

a) K_{\textrm{p}} = \dfrac{p^{2}(\ce{NH3})}{p^{3}(\ce{H2})\cdot p(\ce{N2})}

b) K_{\textrm{p}} = \dfrac{p^{2}(\ce{SO3})}{p^{2}(\ce{SO2})\cdot p(\ce{O2})}

c) K_{\textrm{p}} = \dfrac{p(\ce{CO})\cdot p(\ce{Br2})}{p(\ce{COBr2})}

d) K_{\textrm{p}} = \dfrac{p(\ce{CO})\cdot p^{3}(\ce{H2})}{p(\ce{CH4})\cdot p(\ce{H2O})}

Jednadžbe napišite uz pomoć alata za Pisanje kemijskih jednadžbi na webu.

Odgovor:

a) \ce{3H2(g) + N2(g) <=> 2NH3(g)}

 
b) \ce{2SO2(g) + O2(g) <=> 2SO3(g)}

 
c) \ce{COBr2(g) <=> CO(g) + Br2(g)}

 
d) \ce{CH4(g) + H2O(g) <=> CO(g) + 3H2(g)}

Osim promjene koncentracije (c) reaktanata i produkata u ovisnosti o vremenu, iz grafikona se mogu odčitati početne i ravnotežne koncentracije.

Osim promjene koncentracije reaktanata i produkata u ovisnosti o vremenu, iz grafikona se mogu odčitati početne i ravnotežne koncentracije.

Fotografija prikazuje grafikon s dva grafa, crveni, plavi. Crveni, uzlazni graf prikazuje ravnotežu koncentracije produkta dok plavi, silazni graf predstavlja ravnotežu koncentracije reaktanta. Dijagram prikazuje promjene koncentracije reaktanata i produkata.
Grafički prikaz ovisnosti promjene koncentracije reaktanata i produkata u ovisnosti o vremenu

Riješeni primjer 1

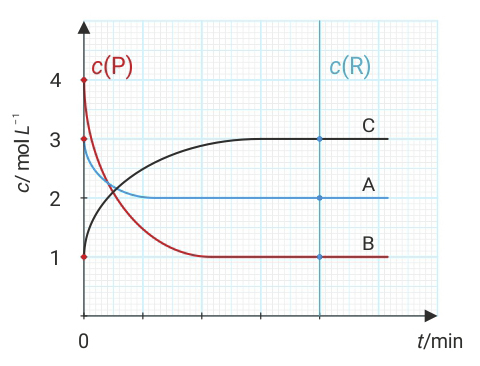
Slika prikazuje ovisnost množinske koncentracije (c) tvari A, B i C u reakcijskoj smjesi stalnog volumena (V) o vremenu (t).

a) Napišite odgovarajuću jednadžbu kemijske reakcije:
b) Izračunajte konstantu ravnoteže (Kc).

Korak 1

Na grafičkom prikazu mogu se očitati početne (cp) i ravnotežne koncentracije (cr) reaktanata i produkata.

Tablica podataka.
cp – početna koncentracija cr – ravnotežna koncentracija
c_\textrm{p}(A) = \pu{3 mol/L} c_\textrm{r}(A) = \pu{2 mol/L}
c_\textrm{p}(B) = \pu{4 mol/L} c_\textrm{r}(B) = \pu{1 mol/L}
c_\textrm{p}(C) = \pu{1 mol/L} c_\textrm{r}(C) = \pu{3 mol/L}

Korak 2

Odgovarajuća jednadžba reakcije može se očitati iz grafičkog prikaza:

\ce{A + 3B <=> 2C}

Korak 3

Na temelju ravnotežnih koncentracija izračuna se vrijednost konstante ravnoteže (Kc):

K_{\textrm{c}} = \dfrac{[\ce{C}]^{2}}{[\ce{A}][\ce{B}]^{3}} = \dfrac{(\pu{3 mol dm-3})^{2}}{\pu{2 mol dm-3}\cdot (\pu{1 mol dm-3})^{3}} = \pu{4,5 dm6 mol-2}

Odgovor:

Konstanta ravnoteže (Kc) iznosi 4,5 dm6 mol-2

Riješeni primjer 1.

Slika prikazuje ovisnost množinske koncentracije tvari A, B i C u reakcijskoj smjesi stalnog volumena o vremenu t.

ovisnost množinske koncentracije tvari A, B i C u reakcijskoj smjesi stalnog volumena o vremenu t.

 
a) Napišite odgovarajuću jednadžbu kemijske reakcije za tvari A, B i C u reakcijskoj smjesi na temelju grafičkog prikaza.
b) Izračunajte konstantu ravnoteže, K_\textrm{c} .

Korak 1

Na grafičkom prikazu mogu se očitati početne i ravnotežne koncentracije reaktanata i produkata.

 

Tablica podataka.
cp – početna koncentracija cr – ravnotežna koncentracija
c_\textrm{p}(A) = \pu{3 mol/L} c_\textrm{r}(A) = \pu{2 mol/L}
c_\textrm{p}(B) = \pu{4 mol/L} c_\textrm{r}(B) = \pu{1 mol/L}
c_\textrm{p}(C) = \pu{1 mol/L} c_\textrm{r}(C) = \pu{3 mol/L}

Korak 2

Odgovarajuća jednadžba kemijske reakcije može se očitati iz grafičkog prikaza:

\ce{A + 3B <=> 2C}

Korak 3

Na temelju ravnotežnih koncentracija izračuna se vrijednost konstante ravnoteže:

K_{\textrm{c}} = \dfrac{[\ce{C}]^{2}}{[\ce{A}][\ce{B}]^{3}} = \dfrac{(\pu{3 mol dm-3})^{2}}{\pu{2 mol dm-3}\cdot (\pu{1 mol dm-3})^{3}} = \pu{4,5 dm6 mol-2}

Odgovor:

Konstanta ravnoteže iznosi 4,5 dm6 mol-2

Zadatak:

Grafikon prikazuje ovisnost množinske koncentracije (c) triju tvari u reakcijskoj smjesi stalna volumena o vremenu t.

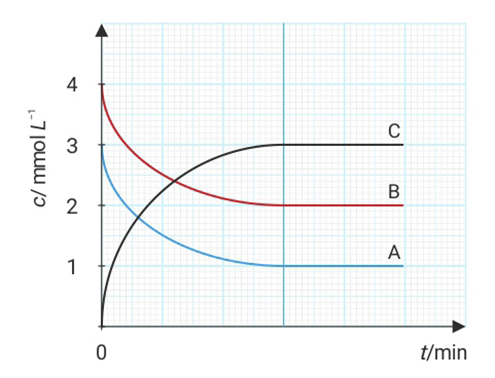
a) Napišite odgovarajuću jednadžbu kemijske reakcije za tvari A, B i C u reakcijskoj smjesi na temelju grafičkog prikaza.

b) Izračunajte konstantu ravnoteže, Kc. Rezultat iskažite na tri značajne znamenke.

Odgovor:

a) \ce{2A + 2B <=> 3C}

b) K_{\textrm{c}} = \pu{6,75 dm3 mol-1}

Zadatak:

Grafikon prikazuje ovisnost množinske koncentracije triju tvari u reakcijskoj smjesi stalna volumena o vremenu t.

a) Napišite odgovarajuću jednadžbu kemijske reakcije za tvari A, B i C u reakcijskoj smjesi na temelju grafičkog prikaza.

b) Izračunajte konstantu ravnoteže, Kc. Rezultat iskažite na tri značajne znamenke.

Odgovor:

a) \ce{2A + 2B <=> 3C}

b) K_{\textrm{c}} = \pu{6,75 dm3 mol-1}

Riješeni primjer 2

U posudi volumena (V) 1 L stavi se 0,25 mola (n) N2O4.
Do uspostavljanja ravnoteže razložilo se 75% (w) početne množine N2O4.
Koliko iznosi konstanta ravnoteže (Kc) navedene reakcije?

\ce{N2O4(g)<=> 2NO2(g)}

Sve promjene tijekom reakcije mogu se dobiti izračunavanjem na osnovi jednadžbe kemijske reakcije.

Zadano je:

V = \pu{1 L}

n_{\textrm{početna}}(\ce{N2O4}) = \pu{0,25 mol}

x = \pu{0,75 \%}

Traži se:

K_\textrm{c} = ?

Napomena:
Za izračunavanje konstante ravnoteže (Kc) potrebne su ravnotežne koncentracije reaktanata i produkata u reakciji.

Izradak:

Jednadžba kemijske reakcije: \ce{N2O4(g)<=> 2NO2(g)}

Do uspostavljanja ravnoteže razložilo se 75 % početne množine \ce{N2O4} :

Potrebno je izračunati koliko se molova \ce{N2O4} razložilo od početne množine:

n(\ce{N2O4})_{\textrm{ravnotežna}} = n(\ce{N2O4})_{\textrm{početna}}\cdot x
n(\ce{N2O4})_{\textrm{ravnotežna}} = \pu{0,25 mol}\cdot \pu{0,75} = \pu{0,19 mol}

Izračuna se množina (n)  \ce{N2O4} u ravnoteži:
n(\ce{N2O4}) = \pu{0,25 mol} -\pu{0,19 mol} = \pu{0,06 mol}
n(\ce{NO2}) = 2\cdot \pu{0,19 mol} = \pu{0,38 mol}

Iz jednadžbe kemijske reakcije je vidljivo da se množina (n)
\ce{N2O4} umanjila za X mola.

Množina (n) \ce{NO2} povećala se za 2X mola.

Tablica podataka
\ce{N2O4(g)} \ce{NO2(g)}
početna množina/mol 0,25 0
promjena –X + 2X
ravnotežna množina/mol 0,06 0,38

 

Budući da je volumen (V) posude 1 L, množine tvari (n) u ravnoteži jednake (=) su njihovim ravnotežnim koncentracijama (c).

Ravnotežne koncentracije (c) su prema tome:

c(\ce{N2O4}) = \pu{0,06 mol dm-3}
c(\ce{NO2}) = \pu{0,38 mol dm-3}

Riješeni primjer 2.

U posudi volumena 1 L stavi se 0,25 mola \ce{N2O4} . Do uspostavljanja ravnoteže razložilo se 75 % početne množine \ce{N2O4} . Koliko iznosi konstanta ravnoteže navedene reakcije?

\ce{N2O4(g)<=> 2NO2(g)}

Sve promjene tijekom reakcije mogu se dobiti izračunavanjem na osnovi jednadžbe kemijske reakcije.

Zadano je:

V = \pu{1 L}

n_{\textrm{početna}}(\ce{N2O4}) = \pu{0,25 mol}

x = \pu{0,75}

Traži se:

K_\textrm{c} = ?

Napomena: Za izračunavanje konstante ravnoteže potrebne su ravnotežne koncentracije reaktanata i produkata u reakciji.

Izradak:

Jednadžba kemijske reakcije:

\ce{N2O4(g)<=> 2NO2(g)}

Do uspostavljanja ravnoteže razložilo se 75 % početne množine \ce{N2O4} :

Potrebno je izračunati koliko se molova \ce{N2O4} razložilo od početne množine:

n(\ce{N2O4})_{\textrm{ravnotežna}} = n(\ce{N2O4})_{\textrm{početna}}\cdot x
n(\ce{N2O4})_{\textrm{ravnotežna}} = \pu{0,25 mol}\cdot \pu{0,75} = \pu{0,19 mol}

Izračuna se množina \ce{N2O4} u ravnoteži:

n(\ce{N2O4}) = \pu{0,25 mol} -\pu{0,19 mol} = \pu{0,06 mol}
n(\ce{NO2}) = 2\cdot \pu{0,19 mol} = \pu{0,38 mol}

Iz jednadžbe kemijske reakcije je vidljivo da se množina \ce{N2O4} umanjila za X mola, a množina \ce{NO2} povećala za 2X mola.

Tablica podataka
\ce{N2O4(g)} \ce{NO2(g)}
početna množina/mol 0,25 0
promjena –X + 2X
ravnotežna množina/mol 0,06 0,38

Odgovor:

Budući da je volumen posude 1 L, množine tvari u ravnoteži jednake su njihovim ravnotežnim koncentracijama. Ravnotežne koncentracije su prema tome:

c(\ce{N2O4}) = \pu{0,06 mol dm-3}

c(\ce{NO2}) = \pu{0,38 mol dm-3}

Riješeni primjer 3.

Konstanta ravnoteže (Kc) za reakciju razlaganja plinovitog jodovodika (HI) na plinoviti vodik (H2) i jod (I2) iznosi 0,08 pri temperaturi (t) od 700 °C.

Izračunajte ravnotežne koncentracije (c, ravnotežna) produkata.

Početna množina (n) jodovodika (HI) 1,5 mol u posudi volumena (V) 1 L.

Zadano je:
K_{\textrm{c}} = \pu{0,08} \\ V = \pu{1 L}

Traži se:
c_{\textrm{ravnotežna}}(\ce{H2}) = ? \\ c_{\textrm{ravnotežna}}(\ce{Cl2}) = ?

Izradak:

Jednadžba reakcije \ce{2HI(g) <–> H2(g) + I2(g)}
početna množina/mol 1,5 0 0
izreagiralo –2X +X + X
ravnotežna množina/mol 1,5 – 2X X

 

Konstanta ravnoteže (Kc) navedene reakcije je:

K_{\textrm{c}} = \frac{[\ce{H2}][\ce{I2}]}{[\ce{HI}]^{2}}

Nakon uvrštavanja ravnotežnih koncentracija reaktanata i produkata u izraz za konstantu ravnoteže, slijedi:

\pu{0,08} = \dfrac{\textrm{x}^{2}}{(\pu{1,5} -2\textrm{X})^{2}}

Riješite kvadratnu jednadžbu.

Od dva rješenja samo jedno je realno.

\pu{0,08}\cdot (\pu{2,25} – 6\textrm{X} + 4\textrm{X}^{2}) = \textrm{X}^{2}
\pu{0,18} – \pu{0,48}\textrm{X} + \pu{0,32}\textrm{X}^{2} = \textrm{X}^{2}
-\pu{0,68}\textrm{X}^{2} – \pu{0,48}\textrm{X} + \pu{0,18} = 0 \quad /(-1)
\pu{0,68}\textrm{X}^{2} + \pu{0,48}\textrm{X} – \pu{0,18} = 0

\textrm{X}_{1} = \pu{0,271} (realno rješenje, jer je dvostruka izreagirana množina manja od početne množine)

\textrm{X}_{2} = \pu{0,977} (nerealno rješenje jer je “dvostruka izreagirana” množina veća od početne množine)

c_{\textrm{ravnotežna}}(\ce{HI}) = \pu{1,5} – (2\cdot \pu{0,271}) = \pu{0,958}

Odgovor:

Ravnotežne koncentracije produkata su:
c_{\textrm{ravnotežna}}(\ce{H2}) = \pu{0,271 mol dm-3} \\ c_{\textrm{ravnotežna}}(\ce{Cl2}) = \pu{0,271 mol dm-3}

Riješeni primjer 3.

Konstanta ravnoteže za reakciju razlaganja plinovitog jodovodika na plinoviti vodik i jod iznosi 0,08 pri temperaturi od 700 °C. Izračunajte ravnotežne koncentracije produkata, ako je početna množina jodovodika 1,5 mol u posudi volumena 1 L.

Zadano je:
K_{\textrm{c}} = \pu{0,08} \\ V = \pu{1 L}

 

Traži se:
c_{\textrm{ravnotežna}}(\ce{H2}) = ? \\ c_{\textrm{ravnotežna}}(\ce{Cl2}) = ?

Izradak:

Jednadžba reakcije \ce{2HI(g) <–> H2(g) + I2(g)}
početna množina/mol 1,5 0 0
izreagiralo –2X +X + X
ravnotežna množina/mol 1,5 – 2X X

 

Konstanta ravnoteže navedene reakcije je:

K_{\textrm{c}} = \frac{[\ce{H2}][\ce{I2}]}{[\ce{HI}]^{2}}

Nakon uvrštavanja ravnotežnih koncentracija reaktanata i produkata u izraz za konstantu ravnoteže, slijedi:

\pu{0,08} = \dfrac{\textrm{x}^{2}}{(\pu{1,5} -2\textrm{X})^{2}}

Riješite kvadratnu jednadžbu. Od dva rješenja samo jedno je realno.

\pu{0,08}\cdot (\pu{2,25} – 6\textrm{X} + 4\textrm{X}^{2}) = \textrm{X}^{2}
\pu{0,18} – \pu{0,48}\textrm{X} + \pu{0,32}\textrm{X}^{2} = \textrm{X}^{2}
-\pu{0,68}\textrm{X}^{2} – \pu{0,48}\textrm{X} + \pu{0,18} = 0 \quad /(-1)
\pu{0,68}\textrm{X}^{2} + \pu{0,48}\textrm{X} – \pu{0,18} = 0

\textrm{X}_{1} = \pu{0,271} (realno rješenje, jer je dvostruka izreagirana množina manja od početne množine)

\textrm{X}_{2} = \pu{0,977} (nerealno rješenje jer je “dvostruka izreagirana” množina veća od početne množine)

c_{\textrm{ravnotežna}}(\ce{HI}) = \pu{1,5} – (2\cdot \pu{0,271}) = \pu{0,958}

Odgovor:

Ravnotežne koncentracije produkata su:
c_{\textrm{ravnotežna}}(\ce{H2}) = \pu{0,271 mol dm-3} \\ c_{\textrm{ravnotežna}}(\ce{Cl2}) = \pu{0,271 mol dm-3}

Na kraju…

RAVNOTEŽA KEMIJSKIH REAKCIJA

\ce{aA + bB <=> cC + dD}

Izraz za koncentracijsku konstantu ravnoteže je:

K_{\textrm{c}} = \dfrac{[\ce{C}]^{\textrm{c}}\cdot [\ce{D}]^{\textrm{d}}}{[\ce{A}]^{\textrm{a}}\cdot [\ce{B}]^{\textrm{b}}}

Zakon o djelovanju masa ili Guldberg – Waageov zakon.

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Pri temperaturi (t) od 20 °C za neku reakciju konstanta ravnoteže (Kc) iznosi 0,0052.

Točan odgovor je:

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Točna tvrdnja za ravnotežnu reakciju je:

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Ako su ravnotežne koncentracije (c) plinova A, B i C, koji reagiraju prema jednadžbi:

\ce{A + 2B <=> C} ;

c (A) = 0,1 mol/dm3,
c (B) = 1 mol/dm3
c (C) = 0,001 mol/dm3,
konstanta ravnoteže (Kc) navedene reakcije iznosi:

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte konstantu ravnoteže (Kc) pri nekoj temperaturi (t) za reakciju:

\ce{H2(g) + I2(g) <=> 2HI(g)}
ako su:

c (H2) = c (I2) = 0,250 mol dm–3
c (HI) = 0,450 mol dm–3.

Kc = ?

 

Odgovor:
Kc =

Netočno
Točno

Klikom odaberite jedan ili više točnih odgovora.

Odaberite sve točne odgovore.

U posudu volumena (V) 1 L stavi se 1 mol PCl5 (n).
X mola PCl5 disocira na PCl3 i Cl2 prema jednadžbi:

\ce{PCl5 <=> PCl3 + Cl2}

Koliko molova PCl5 i PCl3 je u posudi kad se uspostavi dinamička ravnoteža?

Točni odgovori su:

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Pri temperaturi od 20 °C za neku reakciju konstanta ravnoteže iznosi 0,0052. Točan odgovor je:

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Točna tvrdnja za ravnotežnu reakciju je:

Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

Ako su ravnotežne koncentracije plinova A, B i C, koji reagiraju prema jednadžbi:

\ce{A + 2B <=> C} ;

c(\ce{A}) = \pu{0,1 mol dm-3} , c(\ce{B}) = \pu{1 mol dm-3} , c(\ce{C}) = \pu{0,001 mol dm-3} ,

konstanta ravnoteže navedene reakcije iznosi:

Netočno
Točno

Unesite odgovore na pripadajuća mjesta.

Dopunite rečenicu.

Izračunajte konstantu ravnoteže pri nekoj temperaturi za reakciju:

\ce{H2(g) + I2(g) <=> 2HI(g)}

ako su navedene ravnotežne koncentracije: c(\ce{H2}) = c(\ce{I2}) = \pu{0,250 mol dm-3} i c(\ce{HI}) = \pu{0,450 mol dm-3} .

(Rezultat iskažite na tri značajne znamenke.)

Rješenje:

Kc =
Netočno
Točno

Klikom odaberite jedan točan odgovor.

Odaberite točan odgovor.

U posudu volumena 1 L stavi se 1 mol \ce{PCl5} .

X mola \ce{PCl5} disocira na \ce{PCl3} i \ce{Cl2} prema jednadžbi:

\ce{PCl5 <=> PCl3 + Cl2}

Koliko molova \ce{PCl5} i \ce{PCl3} je u posudi kad se uspostavi dinamička ravnoteža?

Netočno
Točno
{{correctPercent}}%

Želite li pokušati ponovo?