Matematika 4 - 4.2 Problem brzine

Prosječna brzina

Za početak izračunajmo njegovu prosječnu brzinu u prvih $10$ sekundi.

Računamo omjer promjene puta i promjene vremena u prvih $10$ sekundi.

$v = \frac{s (10) - s (0)}{10 - 0} = \frac{120}{10} = 12 m/s$

Kolika je prosječna brzina između devete i desete sekunde?

$1.2 \cdot 10^{2} - 1.2 \cdot 9^{2} =$
$v_{1} =$
$\frac{s (10) - s (9)}{10 - 9} =$
$22.8 m/s$

null

Kolika je prosječna brzina između desete i jedanaeste sekunde?

$1.2 \cdot 11^{2} - 1.2 \cdot 10^{2} =$
$\frac{s (11) - s (10)}{11 - 10} =$
$25.2 m/s$
$v_{2} =$

null

Prosječna brzina – trenutna brzina

Očito je trenutna brzina u desetoj sekundi između $22.8 m/s$ i $25.2 m/s .$

Istražimo

Ako želimo odrediti trenutnu brzinu u $t = 10 s,$ moramo računati prosječne brzine u manjim intervalima koji su dovoljno blizu $t = 10 s .$

Prepišite sljedeću tablicu u bilježnicu i popunite je.

vremenski interval širina intervala u $s$ prosječna brzina u $m/s$

$[9.9, 9.99]$ $0.09$

$[9.99, 9.999]$

$[9.999, 10]$

$[10, 10.001]$

$[10.001, 10.01]$

$[10.01, 10.1]$

Što možete zaključiti za iznos prosječne brzine?

vremenski interval	širina intervala u $s$	prosječna brzina u $m/s$
$[9.9, 9.99]$	$0.09$	$23.868$
$[9.99, 9.999]$	$0.009$	$23.9868$
$[9.999, 10]$	$0.001$	$23.9988$
$[10, 10.001]$	$0.001$	$24.0012$
$[10.001, 10.01]$	$0.009$	$24.0132$
$[10.01, 10.1]$	$0.09$	$24.132$

Što su širine intervala oko $t = 10 s$ manje, to je iznos prosječne brzine bliži $24 m/s .$ Možemo reći da prosječne brzine teže broju $24 m/s$ kada širine intervala teže nuli.

Pokažimo da je trenutna brzina u trenutku $t = 10 s$ jednaka $24 m/s .$

Označimo širinu vremenskoga intervala $Δ t = t - 10,$ pa je $t = 10 + Δ t .$

Promjena puta je $\begin{array}{l} Δ s = s (t) - s (10) = s (10 + Δ t) - s (10) \end{array} .$

$Δ t$ zovemo prirast vremena, a $Δ s$ prirast puta.

Računali smo prosječnu brzinu $\frac{Δ s}{Δ t} = \frac{s (10 + Δ t) - s (10)}{Δ t}$ i smanjivali vremenski interval $Δ t .$ Što je širina vremenskoga intervala $Δ t$ manja, to je prosječna brzina bliža graničnoj vrijednosti od $24 m/s .$

Zbog toga će trenutna brzina u desetoj sekundi biti jednaka $\lim_{Δ t \to 0} \frac{Δ s}{Δ t} = \lim_{Δ t \to 0} \frac{s (10 + Δ t) - s (10)}{Δ t} .$

Izračunajmo ovaj limes:

$\begin{array}{ll} \underset{}{\lim_{Δ t \to 0}} \frac{Δ s}{Δ t} & = \lim_{Δ t \to 0} \frac{s (10 + Δ t) - s (10)}{Δ t} = \lim_{Δ t \to 0} \frac{1.2 {(10 + Δ t)}^{2} - 1.2 \cdot 10^{2}}{Δ t} = \\ = \lim_{Δ t \to 0} \frac{1.2 [100 + 20 Δ t + {(Δ t)}^{2}] - 1.2 \cdot 100}{Δ t} = \lim_{Δ t \to 0} \frac{1.2 [20 Δ t + {(Δ t)}^{2}]}{Δ t} = \\ = \lim_{Δ t \to 0} \frac{1.2 Δ t (20 + Δ t)}{Δ t} = \lim_{Δ t \to 0} 1.2 (20 + Δ t) = 24 \end{array}$

Trenutna brzina u desetoj sekundi iznosi $24 m/s .$

Pogledajmo u animaciji.

Omjerom

\frac{Δ s}{Δ t} = \frac{s (t + Δ t) - s (t)}{Δ t}

računamo

brzinu

u proizvoljnom vremenskom intervalu

Δ t .

Ako taj interval smanjujemo, vrijednosti se prosječnih brzina približavaju

brzini

u trenutku

t .

null

Ako želimo izračunati trenutnu brzinu u bilo kojem trenutku $t \in [0, 15],$ trebamo izračunati:

$\begin{array}{ll} \lim_{Δ t \to 0} \frac{Δ s}{Δ t} & = \lim_{Δ t \to 0} \frac{s (t + Δ t) - s (t)}{Δ t} = \lim_{Δ t \to 0} \frac{1.2 {(t + Δ t)}^{2} - 1.2 t^{2}}{Δ t} = \\ = \lim_{Δ t \to 0} \frac{1.2 [t^{2} + 2 t Δ t + {(Δ t)}^{2}] - 1.2 t^{2}}{Δ t} = = \lim_{Δ t \to 0} \frac{1.2 [2 t Δ t + {(Δ t)}^{2}]}{Δ t} = \\ = \lim_{Δ t \to 0} \frac{1.2 Δ t (2 t + Δ t)}{Δ t} = \lim_{Δ t \to 0} (2.4 t + 1.2 Δ t) = 2.4 t \end{array}$

Zadatak 1.

Trenutna brzina biciklista u trenutku $t = 5 s$ iznosi

6 m/s

12 m/s

18 m/s

20 m/s

null

Zanimljivost

Problemom brzine bavio se engleski matematičar Isaac Newton, koji je uočio povezanost brzine i puta. Njegovo prvo otkriće bila je matematička metoda koju je nazvao fluksija, a danas je poznata kao diferencijalni račun.

...i na kraju

Iz poznate ovisnosti prijeđenoga puta o vremenu dobili smo trenutnu brzinu kao funkciju vremena računajući limes $v (t) = \lim_{Δ t \to 0} \frac{Δ s}{Δ t} = \lim_{Δ t \to 0} \frac{s (t + Δ t) - s (t)}{Δ t} .$

Podsjetite se problema tangente. Uočavate li vezu između tih dvaju problema?

Čemu je jednak $\frac{Δ f}{Δ x} ?$

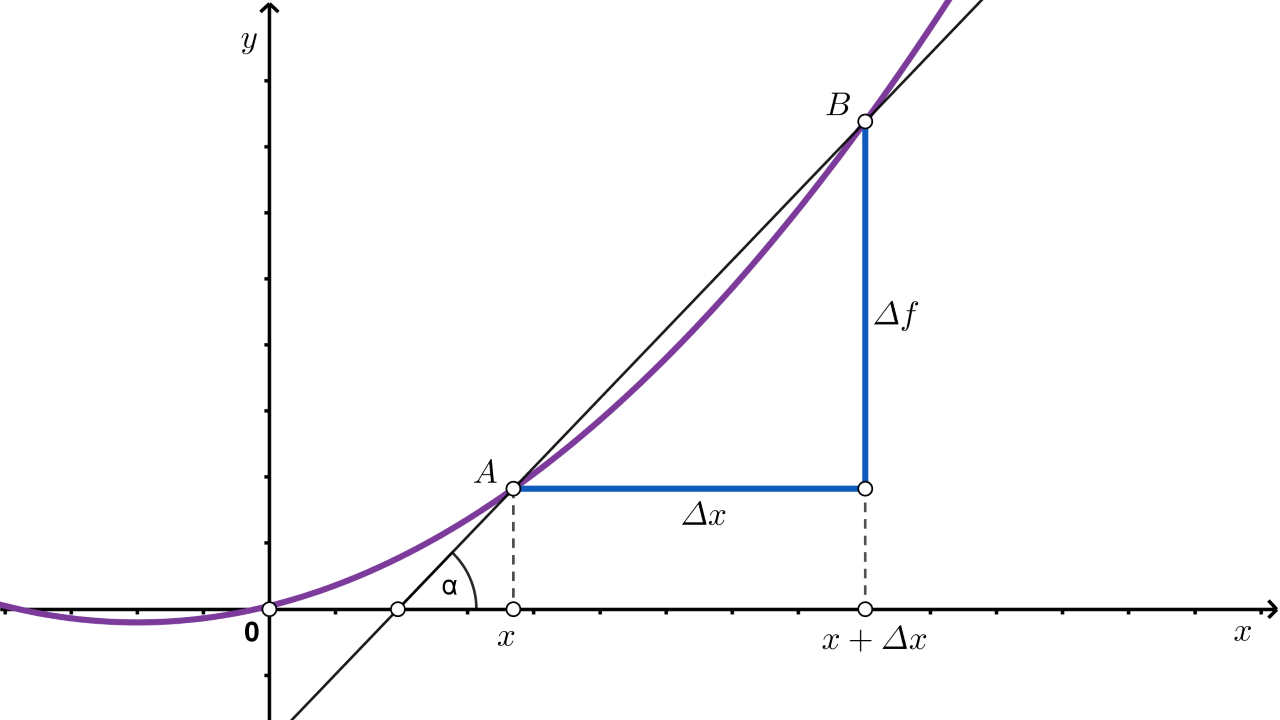
Geometrijska interpretacija limesa omjera prirasta funkcije i prirasta argumenta — Omjer prirasta funkcije i prirasta argumenta

U oba se problema računa limes omjera prirasta funkcije i prirasta argumenta.

Kod problema tangente taj je limes jednak koeficijentu smjera tangente u nekoj točki, a kod problema brzine limes je jednak trenutnoj brzini u nekome trenutku.

$\frac{Δ f}{Δ x} = tg α,$ a $α$ je kut što ga pravac koji prolazi točkama $A$ i $B$ zatvara s pozitivnim smjerom osi apscisa.

U sljedećoj ćemo jedinici problem tangente i problem trenutne brzine povezati s pojmom derivacije.

Na početku...

Prosječna brzina

Prosječna brzina – trenutna brzina

Istražimo

Zadatak 1.

Zanimljivost

...i na kraju