

Statistika i statistički podatci potrebni su nam od davnina. U početku su se popisivali samo poljoprivredni prinosi, stanovništvo i materijalna dobra. S razvojem znanosti i informatike razvila se i statistika kao posebna grana matematike. Danas se primjenjuje u ekonomiji, medicini, sportu, psihologiji, meteorologiji, demografiji, obrazovanju i slično.
Statistički podatci se promatraju, tumače, interpretiraju i analiziraju. Na osnovi analiziranih podataka donose se razne odluke. Primjerice, u nekom restoranu vlasnici bilježe koja jela gosti najviše naručuju pa prema tome znaju kojih namirnica trebaju više nabaviti, a kojih manje.
Već smo naučili crtati razne dijagrame, računati aritmetičku sredinu, odrediti frekvenciju i relativnu frekvenciju.
Volite li skupljati sličice? Analizirajte dijagram s brojem sličica s pticama u paketićima sličica životinja. U svakom je paketiću
sličica različitih životinja. Možete kupiti između
i
paketića.
Nakon što odaberete broj paketića, na dijagramu će biti prikazano u koliko od tih kupljenih paketića nema ni jedna sličica s pticama, u koliko paketića ima jedna sličica s pticama, u koliko dvije itd.
Najprije očitajte najveću frekvenciju, tj. najveći broj paketića s određenim brojem sličica s pticama. Dobro pogledajte u koliko najviše kupljenih paketića ili uopće nema sličica s pticama ili ima jedna ili su dvije itd.
Potom pogledajte u koliko paketića ima koliko sličica s pticama.
Zatim izračunajte prosječni broj sličica s pticama po kupljenom paketiću. Prosječni broj sličica s pticama po kupljenom paketiću računa se kao količnik ukupnog broja sličica s pticama i ukupnog broja kupljenih paketića.
Rješenje provjerite u interaktivnoj simulaciji.
Primjer 1.
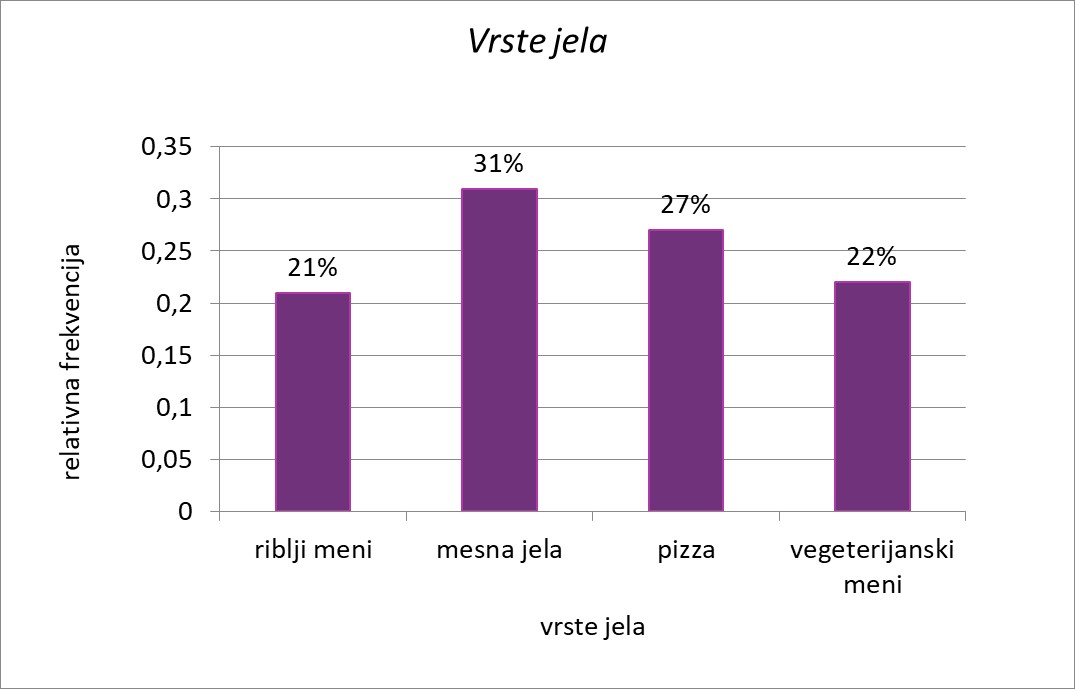
Ivo je vlasnik restorana. Pratio je dnevne narudžbe pojedinih jela. Narudžbi je bilo Izradio je tablicu frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.
Vrsta mesa Frekvencija Relativna frekvencija Relativna frekvencija
u obliku postotkariblji meni mesna jela pizza vegeterijanski meni zbroj
- Nacrtajmo u bilježnicu stupčasti dijagram relativnih frekvencija s pomoću te tablice.
- Koje su vrste jela gosti najviše naručivali?
- Koliki je postotak naručivanja ribljih jela?
- Koje proizvode vlasnik treba nabavljati ako želi zadovoljne goste?
Stupčasti dijagram relativnih fekvencija je stupčasti dijagram kojem su na osi relativne frekvencije pojedinih vrijednosti.
Hrvatski lovački savez imao je lovaca 2011. godine, lovaca 2012. godine, lovaca 2013. godine, lovca 2014. godine te lovaca 2015. godine.
Izvor: Državni zavod za statistiku, Statistički ljetopis 2016.
a. Tablica frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.
| Godina | Frekvencija | Relativna frekvencija | Relativna frekvencija u obliku postotka |
|---|---|---|---|
| 2011. | |||
| 2012. | |||
| 2013. | |||
| 2014. | |||
| 2015. | |||
| Zbroj |
b. Nacrtajte stupčasti dijagram relativnih frekvencija.
c. Najviše je lovaca bilo 2013. godine.
d. Od 2011. do 2013. godine broj lovaca se povećavao, a od 2013. do 2015. godine broj lovaca se smanjivao.
Primjer 2.
Na Olimpijskim igrama 2016. u Rio de Janeiru Hrvatska olimpijska ekipa osvojila je zlatnih, srebrne i brončane medalje. Od mjesta naša je ekipa bila na 17. mjestu po uspješnosti.
- Prikažimo u bilježnicu podatke tablicom frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.
- Nacrtajmo u bilježnicu kružni dijagram relativnih frekvencija u obliku postotka. Prisjetimo se da se središnji kut kružnih isječaka relativnih frekvencija računa tako da se relativne frekvencije u obliku postotka pomnože s 360°.
- Koliko smo ukupno osvojili medalja na tim Olimpijskim igrama? Saznajte koji su to bili sportovi i sportaši.
- Na Olimpijskim igrama su te godine osvojene ukupno medalje. Najuspješnija ekipa, SAD, osvojila je medalju. Koliki je postotak našeg broja osvojenih medalja u odnosu prema ukupnom broju osvojenih medalja na tim Olimpijskim igrama ? Koliki je postotak medalja osvojila ekipa iz SAD-a?
a.
Tablicu frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.
| Vrsta medalje |
Broj medalja |
Relativna frekvencija |
Relativna frekvencija u obliku postotka |
|---|---|---|---|
| zlatna medalja |
|||
| srebrna medalja |
|||
| brončana medalja |
b. Kružni dijagram relativnih frekvencija crta se kao i svaki drugi kružni dijagram ‒ svakoj relativnoj frekvenciji pridružimo kružni isječak.
c. Ukupno smo osvojili medalja.
d. Postotak broja naših medalja u odnosu prema svim osvojenim medaljama je
U kružnom dijagramu relativnih frekvencija svakoj relativnoj frekvenciji pridružimo kružni isječak. Središnji kut koji pripada kružnom isječku određene relativne frekvencije računa se kao umnožak relativne frekvencije u obliku postotka s
Godine 2015. osnovnu je školu završio učenik, -ero učenika završilo je srednju školu, student završio je stručni studij i -ero studenata završilo je sveučilišni studij.
Izvor: Državni zavod za statistiku, Statistički ljetopis 2016.
a. Prikažimo u bilježnicu podatke tablicom frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka.
b. Nacrtajmo u bilježnicu kružni dijagram relativnih frekvencija.
c. Koliko je ukupno učenika i studenata završilo škole i fakultete 2015. godine?
a. Tablica frekvencija, relativnih frekvencija i relativnih frekvencija u obliku postotka
| Vrsta završenog stupnja obrazovanja | Frekvencija | Relativna frekvencija | Relativna frekvencija u obliku postotka |
|---|---|---|---|
| osnovna škola | |||
| srednja škola | |||
| stručni studij |
|||
| sveučilišni studij | |||
| zbroj |
c. Ukupan broj učenika i studenata koji su 2015. godine završili škole i fakultete je
Pomoć:
Pogledajte tablicu kako biste pronašli odgovor.
Odgovor napišite u obliku cijelog broja na za to predviđeno mjesto.
Vodostaji rijeka mjere se svaki sat na određenim mjernim postajama. Normalno stanje je vodostaj do
od
proglašava se pripremno stanje obrane od poplave. Sljedeći stupanj su redovite mjere obrane od poplave pa izvanredne, a kad vodostaj dosegne razinu iznad
proglašava se izvanredno stanje.
Na taj se način Hrvatske vode brinu za sigurnost ljudi i imovine u područjima uz rijeke.
Više o vodostajima rijeka možete saznati na stranicama Hrvatskih voda.
U dijagramu je prikazan vodostaj neke rijeke u jednom danu, od
sati do
sati.
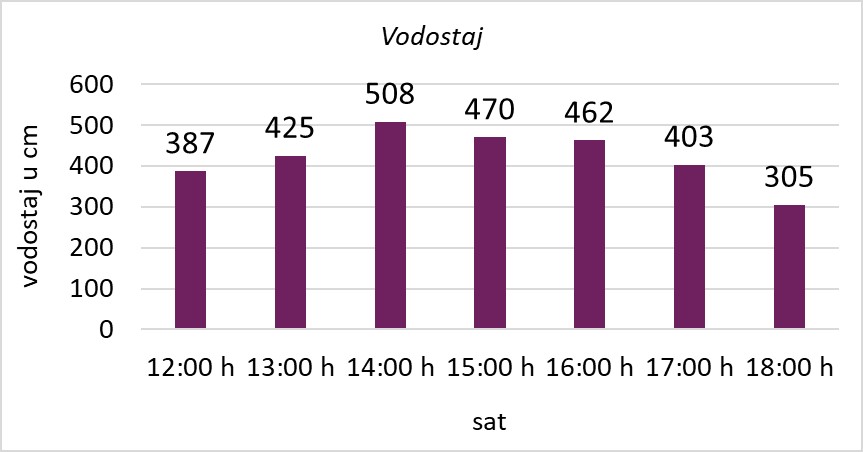
Iz prosječne vrijednosti nismo mogli zaključiti da je u tom razdoblju bilo opasnosti od poplave. Mogli smo samo vidjeti da je vodostaj bio povišen.
Kada promatramo cjelovite podatke, primjerice vodostaj tijekom deset godina, bilo bi komplicirano pratiti vodostaj svaki sat svakoga dana tijekom tog razdoblja. Obično nam ti podatci trebaju za neke analize i usporedbe pa uzimamo prosječnu vrijednost u pojedinim tjednima, mjesecima ili godinama.
Planirate ići na izlet u Rijeku. Pogledajte dijagram prosječnih padalina tijekom 2015. i 2016. godine i odgovorite na pitanja. (Izvor podataka: DHMZ)
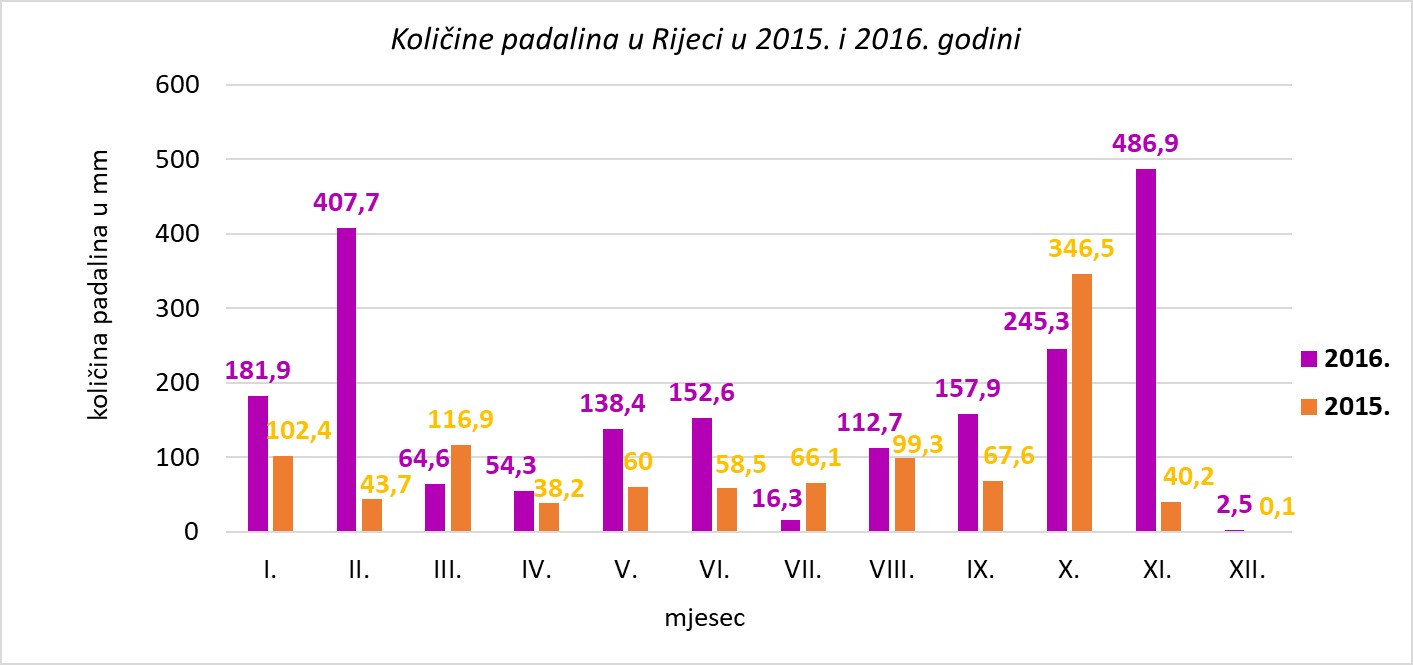
Obje godine je u prosincu bilo najmanje padalina, što vidimo iz stupčastog dijagrama.
Nije dovoljno promatrati samo dvije uzastopne godine da bi se to moglo pretpostaviti. Nekada davno ljudi su izrađivali godišnjake i stogodišnjake i iz njih uspoređivali podatke. Danas možemo podatke pronaći na internetu, konkretno za ovaj zadatak na stranici DHMZ-a, Ukupne oborine.
Na stranicama DZS-a možete pronaći mnoštvo podataka u Statističkim ljetopisima.
Ne možemo znati je li 12. prosinca 2015. godine u Rijeci bilo padalina jer su u dijagramu prikazani prosječni mjesečni podatci.
Nije sigurno kakvo će biti vrijeme 12. prosinca ove godine. Kada bismo pogledali podatke za taj datum za primjerice svaku od 100 godina unazad, mogli bismo pretpostaviti hoće li biti padalina, ali ni tada ne bismo bili sigurni u to.
Takva vrsta stupčastog dijagrama naziva se višestruki stupčasti dijagram. Tim se dijagramom koristimo kada želimo usporediti podatke za više godina, više razreda i slično. U kojoj se situaciji pogodno koristiti kojim dijagramom, pročitajte na mrežnim stranicama
Matematika na dlanu profesorice Antonije Horvatek.
Ako vas zanima kako se uzima uzorak za statističke podatke, pogledajte sljedeći videozapis DZS-a iz serijala Mala škola statistike – Uzorak.
Stupčastim dijagramom prikazani su podatci o prosječnim dnevnim temepraturama za srpanj 2017. godine te povijesni prosjek za srpanj (prosječna vrijednost temperatura u srpnju tijekom svih godina od kada se bilježe podatci ‒ od 1880. godine). Pogledajte dijagram i odgovorite na pitanja.
Izvor: Državni hidrometeorološki zavod
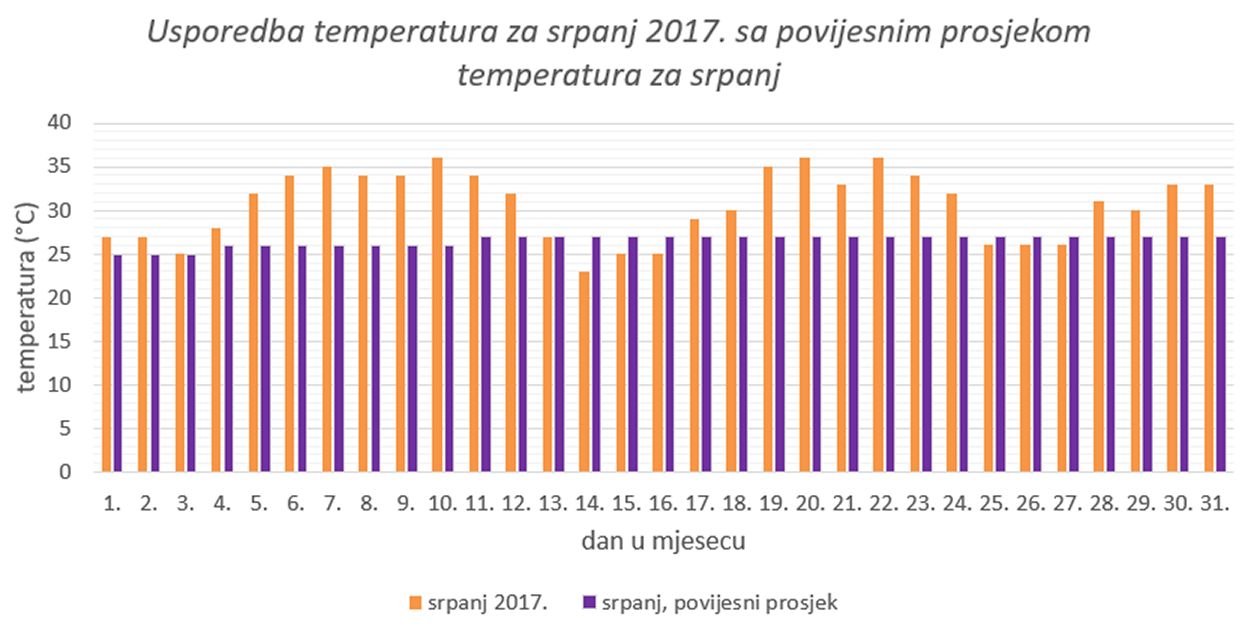
Pomoć:
Pažljivo pogledajte dijagram i odgovorite na pitanja.
Povucite odgovore na predviđena mjesta.
b. Temperature u srpnju 2017. za nekoliko su stupnjeva iznad povijesnog prosjeka. Ako su temperature lipnja i kolovoza 2017. također iznad povijesnog prosjeka, možemo govoriti o jednom od najtoplijih ljeta u povijesti.
Stupčastim dijagramom prikazana je usporedba opožarene površine državnih šuma u odnosu prema ukupnoj opožarenoj površini šuma u Republici Hrvatskoj. Pogledajte sliku i odgovorite na pitanja. (Izvor: DZS)
Pomoć:
Godinu upišite brojčano. Pozorno pogledajte stupčasti dijagram. Odgovore upišite u obliku cijelih brojeva na za to predviđeno mjesto.
U stupčastom dijagramu relativnih frekvencija prikazani su podatci o tome koliko mladih između 18 i 34 godine u Europi živi s roditeljima, za godine od 2010. do 2016. (Izvor: Eurostat)
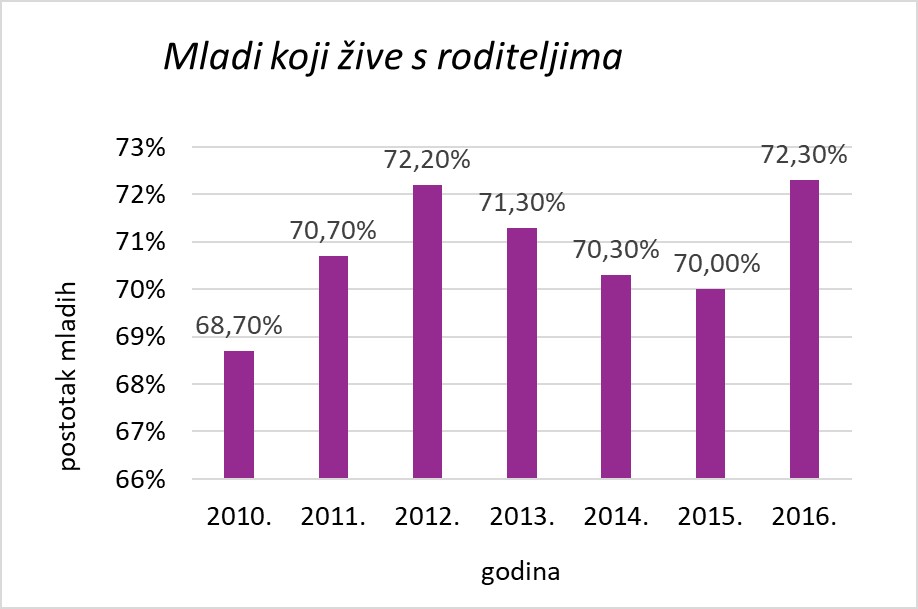
a. Ne, u dijagramu su samo postoci.
b. Tablica relativnih frekvencija.
| Godina | Postotak mladih |
|---|---|
c. Od do je trend rasta, od do je trend pada i onda od do opet raste postotak mladih u dobi između i godine koji žive s roditeljima.
U dijagramima su prikazani brojevi zaposlenih osoba u nekim sektorima u RH u 2013. godini i iznosi prosječnih plaća u tim sektorima u 2013. godini zaokruženi na tisućice. (Izvor: DZS)
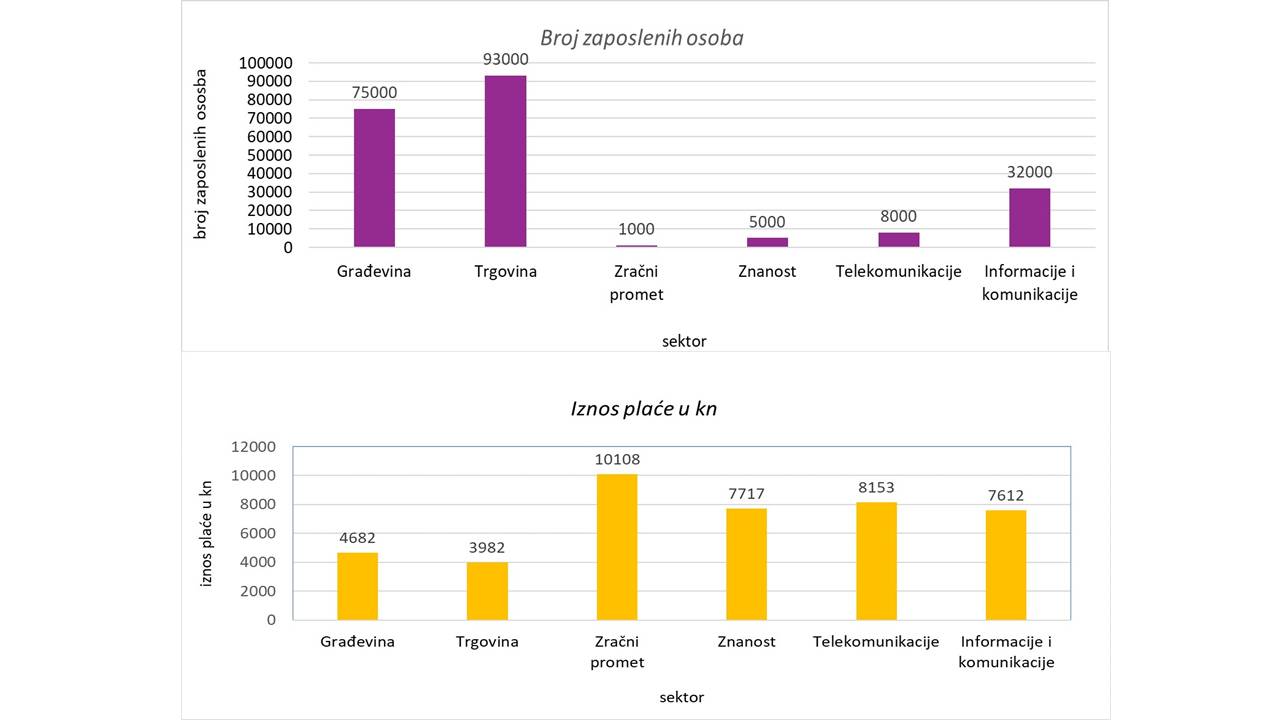
Na slici je prikazan kružni dijagram. Pozorno ga pogledajte i odgovorite na pitanja. (Izvor: DZS)
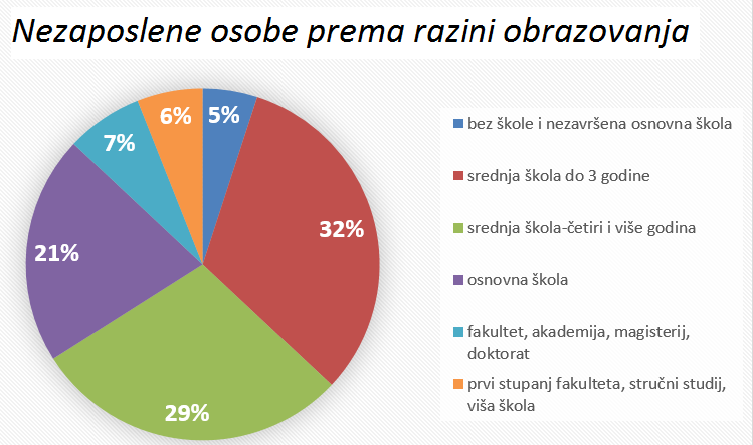
U tablici su podatci o zastupnicima Hrvatskog sabora prema strankama koje su predlagale izborne liste na izborima u rujnu 2016. godine (Izvor podataka: Državno izborno povjerenstvo).
| Lista | Broj zastupnika |
|---|---|
| HDZ | |
| SDP, HNS, HSS, HSU | |
| Most nezavisnih lista ‒ MOST | |
| IDS, PGS, RI | |
| Bandić Milan 365 ‒ stranka rada i solidarnosti, REFORMISTI, NOVI VAL, HSS-SR, BUZ | |
| HDSSB, HKS | |
| Živi zid, Promijenimo Hrvatsku, Akcija mladih, Abeceda demokracije | |
| Neovisna lista | |
| Nacionalne manjine |
a. Izračunajte relativne frekvencije u obliku postotka pojedinih lista.
| Lista | Broj zastupnika | Relativna frekvencija | Relativna frekvencija u obliku postotka |
|---|---|---|---|
| HDZ | |||
| SDP, HNS, HSS, HSU | |||
| Most nezavisnih lista - MOST | |||
| IDS, PGS, RI | |||
| Bandić Milan 365 ‒ stranka rada i solidarnosti, REFORMISTI, NOVI VAL, HSS-SR, BUZ | |||
| HDSSB, HKS | |||
| Živi zid, Promijenimo Hrvatsku, Akcija mladih, Abeceda demokracije | |||
| Neovisna lista | |||
| Nacionalne manjine | |||
| Zbroj |
|
b. Nacrtajte
u bilježnicu
pripadni stupčasti dijagram relativnih frekvencija.
Hrvatski sabor je predstavničko tijelo građana i nositelj zakonodavne vlasti u Republici Hrvatskoj. Broj zastupnika određen je Zakonom o izboru zastupnika u Hrvatskoj i oni se biraju tajnim glasovanjem. Zastupnici se biraju na mandat od četiri godine. Ovaj, deveti saziv Hrvatskog sabora, konstituiran je na temelju izbora za zastupnike održanih 11. rujna 2016. godine. Na temelju glasova građana u Sabor je izabran
zastupnik.
Znate li točne nazive svih stranaka koje su izabrane u Hrvatski sabor 2016. godine?

Iz dnevnih novina izrezujte dijagrame i statističke podatke. Skupite ih i ponesite u školu. Podijelite se u skupine i jedni drugima objasnite svoje dijagrame. Izradite plakat na koji ćete staviti dijagrame i njihova tumačenja. Nacrtajte i svoje dijagrame (takve podatke prikazujemo stupčastim dijagramom).
Razmislite prikazuju li dijagrami podatke nepristrano ili posebno ističu neko stajalište ili stranu. Sjetite se provjeriti podatke iz medija tako da pronađete još neki izvor koji govori o tim podatcima. Više različitih mišljenja pomoći će vam da stvorite širu sliku o nekom događaju ili pojavi.
Potražite informacije o filter mjehuriću ‒ tako se naziva efekt kad nam mrežni pretraživači prikazuju samo one informacije koje smatraju važnijim za nas te tako ograničavaju informacije koje vidimo.
Grgur je učenik 7. razreda. Na kraju školske godine njegove ocjene iz Matematike bile su:
,
,
,
,
,
,
,
,
,
,
,
i
.
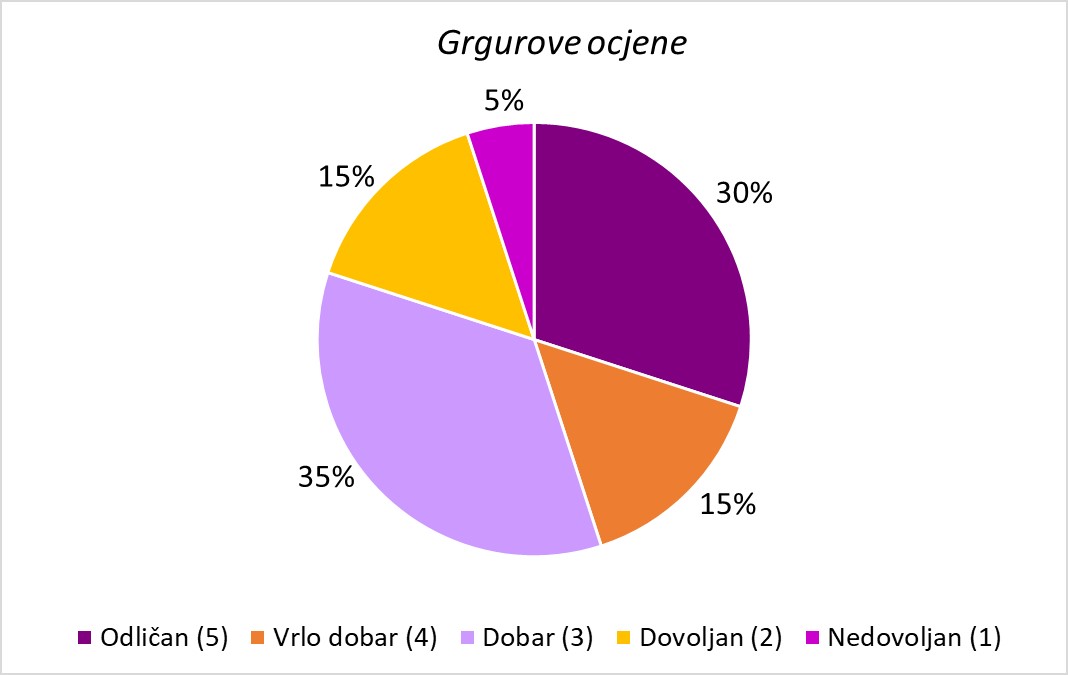
| Ocjene | Broj ocjena | Relativne frekvencije | Relativne frekvencije u obliku postotka |
|---|---|---|---|
| odličan | |||
| vrlo dobar | |||
| dobar | |||
| dovoljan | |||
| nedovoljan | |||
| zbroj |
c. Ukupno je dobio ocjena.
d. Najviše je bilo ocjena dobar ( ).
e. Prosječna ocjena tog učenika iz Matematike je
f. Zaključna mu je ocjena vrlo dobar
g. Bio je vrlo blizu ocjeni dobar ( ).
h. ocjena mu je bilo više od prosječne
i. Ne može jer nemamo uvid u imenik i bilješke, imamo samo ispisane brojčane ocjene.
Dijagramima je prikazan broj učenika i broj razrednih odjela u osnovnim školama. Pogledajte dijagrame i odgovorite na pitanja.
(Izvor: DZS)
Državni pedagoški standard osnovnoškolskog sustava odgoja i obrazovanja propisuje broj učenika u razrednom odjelu od do Iznimno, zbog posebnih okolnosti, razredni odjel može imati više od i manje od učenika. Primjerice, ako u razredu ima učenika s posebnim potrebama, u razrednom odjelu može biti i manje od učenika.
Optimalan broj učenika u jednom razrednom odjelu je
Koliko je učenika u vašemu razrednom odjelu?
Istražite koliko učenika ima u pojedinom 7. razredu u vašoj školi. Izradite u bilježnicu linijski dijagram kojim ćete prikazati te podatke.
Godine 2015. u Hrvatskoj je bilo
osoba u postupku stjecanja doktorata znanosti na visokim učilištima.
(Izvor: DZS)
. Pogledajte kružni dijagram i odgovorite koliko je žena bilo u tom postupku?
Pozorno pogledajte dijagram i povucite podatke na odgovarajuće točke.
Povucite podatke na odgovarajuću točku linijskog dijagrama.
Pomoć:
Pažljivo pogledajte dijagram. Podatke povucite na točku.
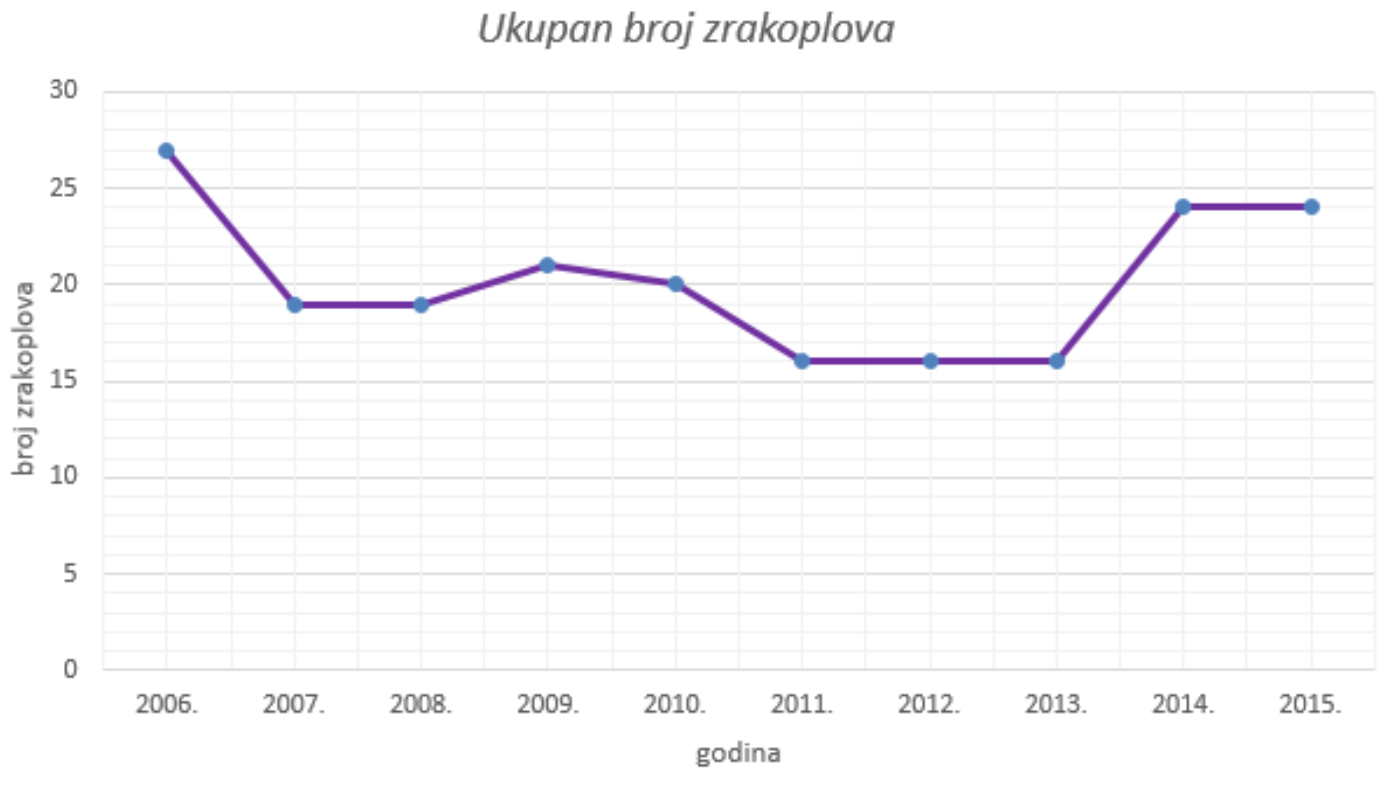
Prikazan je linijski dijagram koji pokazuje broj zrakoplova u Hrvatskoj.
(Izvor: DZS)
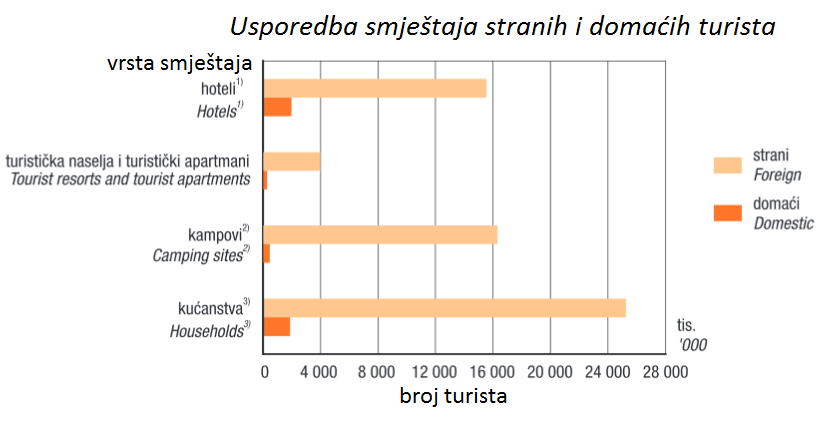
Pogledajte dijagram i odgovorite na pitanja. (Izvor: DZS)
Na parkiralištu su parkirani automobili s registarskim oznakama gradova VU, OS, OS, OS, ZD, ZD, ŠI, ŠI, ZD, ZG, ZG, ZD, ZD, ZD, ZD, OS, ZG, ZG, ŠI, ZD, OS, ŠI, ŠI, ZG, ZG, NA, NA, NA, VU, VU, ZD, ZD, ZD, ZD, OS, ZD, ZD, ZD, ŠI, ZD, ZD, ZD i ZD.
a. Tablica frekvencija, relativnih frekvencija i relativnih frekvencija
| Registarska oznaka grada |
Frekvencija |
Relativna frekvencija |
Relativna frekvencija u obliku postotka |
|---|---|---|---|
| VU | |||
| OS | |||
| ZD |
|||
| ŠI |
|||
| NA |
|||
| ZG |
|||
| Ukupno |
b. Odabrat ćemo kružni dijagram. Našičkih oznaka ima
od svih registarskih tablica na tom parkiralištu.
c. Pretpostavit ćemo da se nalazimo u Zadru ili okolici, s obzirom na to da je na parkiralištu najviše zadarskih tablica. Isto tako, s obzirom na to da je na parkiralištu i velik broj kontinentalnih tablica, možemo pretpostaviti da su tablice zapisivane tijekom ljeta.
d. Stupčasti dijagram frekvencija
e. Kružni dijagram relativnih frekvencija u obliku postotka
Dva sata pratite registarske oznake na automobilskim tablicama pokraj najprometnije prometnice u svojemu mjestu ili pokraj najvećeg parkirališta. Zapisujte nazive gradova ili država na automobilskim tablicama koje ne pripadaju vašemu mjestu. Izradite tablicu frekvencija i dijagram frekvencija te saznajte iz kojega grada (ili države) u vaš grad dolazi najviše automobila.
Marko je odlučio izrađivati adventske vijence za prodaju. Odlučio je voditi evidenciju o izradi s pomoću tablica i dijagrama. Nije siguran koji dijagram izabrati. Pogledajte videozapis Koji dijagram je najbolji i pomozite Marku riješiti dvojbu.
Povežite podatke s dijagramima.
Za svaki dijagram pronađite podatke koji se s pomoću njega mogu najbolje očitati.
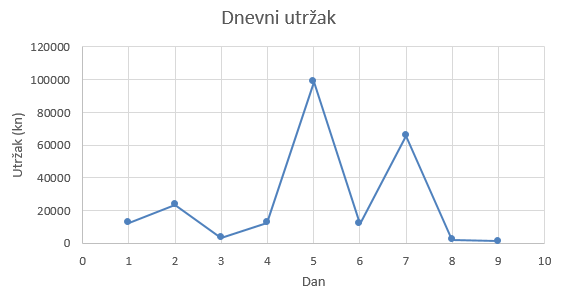
|
|
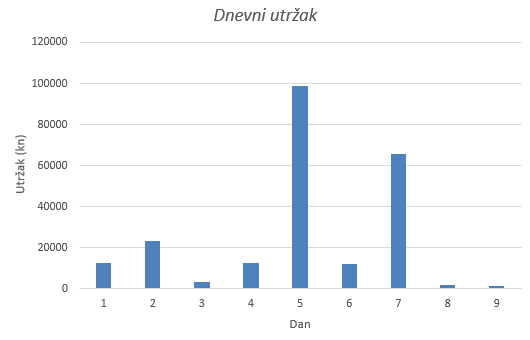
|
|
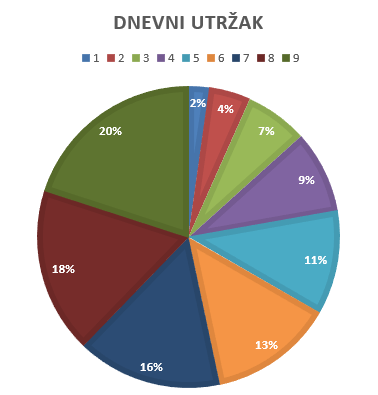
|
Pomoć:
Najveći i najmanji dnevni utržak vrlo se lako u ovome slučaju mogu iščitati iz linijskog i stupčastog dijagrama, međutim linijski dijagram puno bolje prikazuje povećanje i smanjenje dnevnog utrška. Udio utrška u odnosu na sve utrške najlakše je prikazati postotkom, te je u tom slučaju primjereniji kružni dijagram.
Učenici jednog razreda su na ispitu iz Matematike, na kojem je ukupno bilo bodova, postigli sljedeće bodove:
, i
a. Koliko je učenika u tom razredu?
b. Ako je kriterij ocjenjivanja ispita dan tablicom, pronađite koliki je broj učenika dobio koju ocjenu?
| Ocjena | Postotak riješenosti ispita |
|---|---|
c. Nacrtajte u bilježnicu stupčasti dijagram. Što možete reći o njemu?
d. Koja je prosječna ocjena razreda?
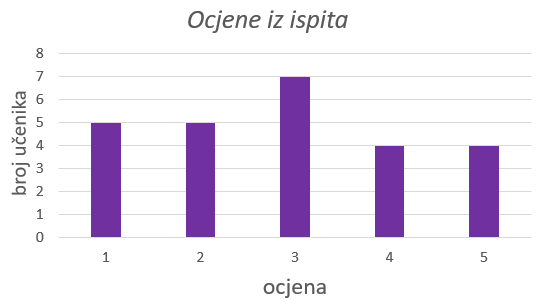
a. Pod pretpostavkom kako ni jedan učenik nije izostao sa sata kada se pisao ispit, u razredu je učenika.
b. Dopunimo tablicu brojem bodova potrebnim za pojedinu ocjenu. Kod gornje granice postotka riješenosti bodove zaokružimo na najbliži manji cijeli broj, kažemo na najmanje cijelo.
| Ocjena | Postotak riješenosti ispita | Bodovi |
|---|---|---|
|
|
Prethodna tablica olakšat će nam grupirati brojeve bodova iz ispita po ocjenama.
| Ocjena | Broj učenika |
|---|---|
d. Prosječnu ocjenu razreda izračunat ćemo primjenom formule za aritmetičku sredinu.
Prosječna ocjena razreda je dobar (
).
U ovoj smo jedinici izdvojili samo neke teme koje su statistički obrađene. Za kraj smo vam dali ideju za mali projekt. Kad ga završite, otiđite s prijateljima u obližnje kino pogledati jedan od filmova koji ste odabrali.
Potražite na internetu popis filmova koji se prikazuju u vašem omiljenom kinu, svakom filmu pridružite broj zvjezdica koje je dobio kao ocjenu. Nacrtajte stupčasti dijagram relativnih frekvencija za te podatke.
Hoće li vam taj dijagram pomoći da se odlučite koji biste film gledali ili ćete naći neki drugi kriterij prema kojem ćete odabrati film, ovisi o vama.