

Pogledajmo dječju igru u parku. Konjići na kojima se djeca igraju imaju elastične opruge na dnu. Što još može imati elastična svojstva osim opruge?
Zamislimo vježbu s elastičnim vrpcama za vježbanje. Jeste li pokušali vježbati s elastičnim vrpcama? Što ste osjećali? Je li bilo lako držati vrpcu u rastegnutom položaju?
Kada na neko tijelo djelujemo silom, ono će promijeniti oblik. Kada rukama rastegnemo elastičnu vrpcu za vježbanje i želimo ju zadržati u tom obliku, osjećat ćemo napor u mišićima i bit će nam izrazito teško zadržati ruke u tom položaju. Elastična vrpca za vježbanje želi se vratiti u prvotni oblik. Javlja se sila koja se suprostavlja sili mišića i ta se sila naziva elastična sila.
Ako djelujemo manjom silom na elastičnu vrpcu za vježbanje, ona će se manje rastegnuti. Ako djelujemo većom silom na vrpcu za vježbanje, ona će se više rastegnuti i više se opirati promjeni oblika.
Elastična sila je sila koja nastoji vratiti tijelo u prvotni oblik.
Elastična sila suprotne je orijentacije od sile koja rasteže elastično tijelo.
Svojstvo tijela da se nakon prestanka djelovanja sile vrati u prvotni oblik naziva se elastičnost.
Tijela katkad pokazuju svojstva elastičnosti do određene granice. Prijeđemo li tu granicu, tijela gube svoja elastična svojstva i neće se vratiti u prvotni oblik. Jeste li se kada igrali malom oprugom iz kemijske olovke? Kada na nju djelujete malom silom, ona će se rastegnuti, ali i vratiti u prvotni oblik i pokazivat će elastična svojstva. Kada na nju djelujete velikom silom i rastegnete je preko njezine granice elastičnosti, ona se više neće vratiti u prvotni oblik. Njezina svojstva više nisu elastična.
Svojstvo tijela da se nakon prestanka djelovanja sile ne vrati u prvotni oblik naziva se plastičnost.
Pogledajmo primjer djelovanja elastične sile na oprugu.
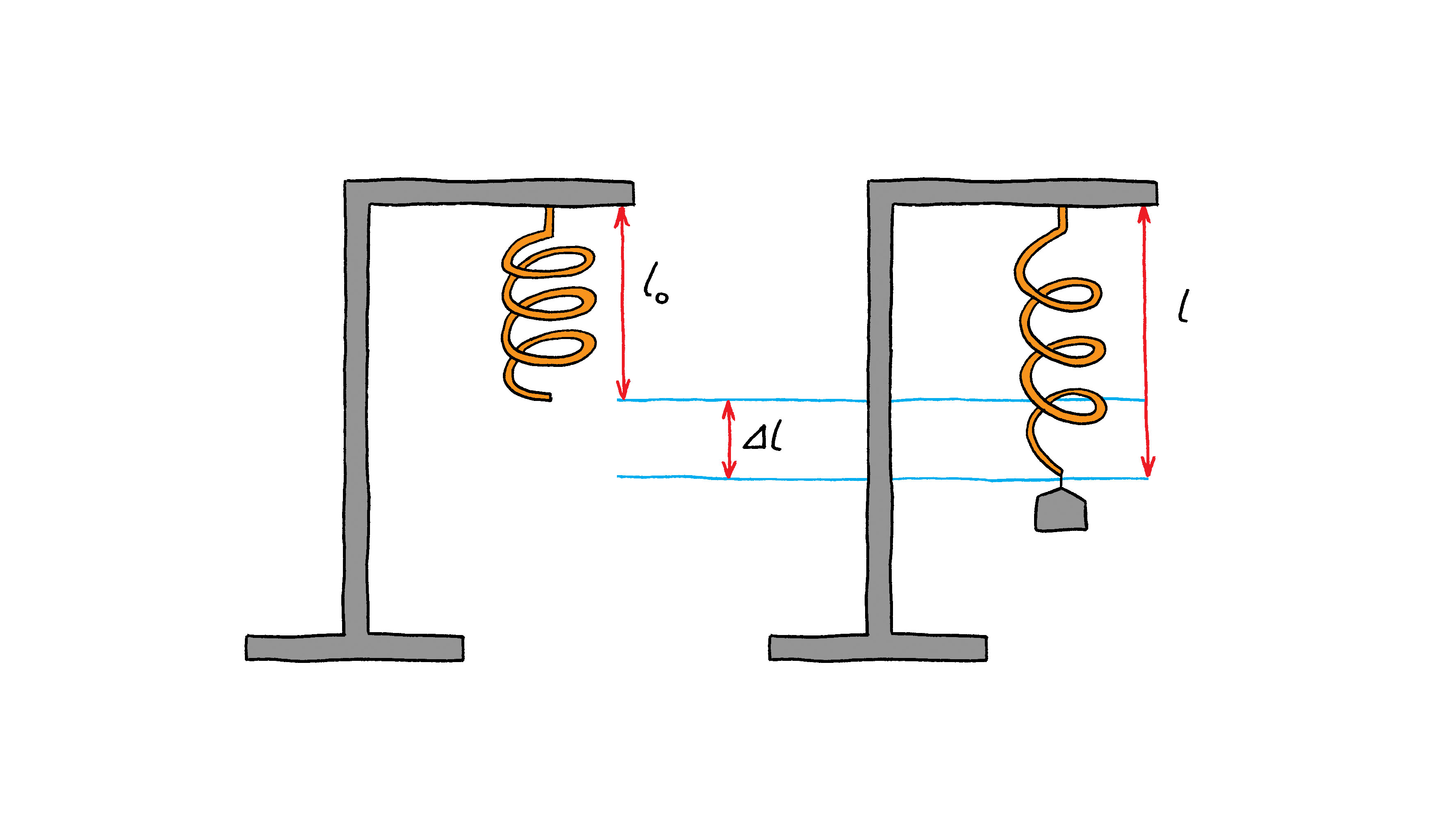
Duljinu nerastegnute opruge označavamo oznakom
Duljinu rastegnute opruge označavamo oznakom
Produljenje opruge jednako je razlici tih dviju duljina i označavamo ga s
Što uočavate?
Kako produljenje opruge ovisi o broju utega?
Uočavate li neku pravilnost?
Što je broj utega jednakih masa veći, veće je i produljenje opruge. Za dvaput veći broj utega jednakih masa, produljenje je dvaput veće. Produljenje opruge razmjerno je broju utega, tj. sili koja djeluje na oprugu.
Produljenje opruge razmjerno je broju utega jednakih masa. Koliko puta povećamo broj utega jednakih masa, toliko je puta i veća sila, a i toliko će puta i produljenje opruge biti veće.
Hookeov zakon: Elastičnu silu iskazujemo izrazom koji se naziva Hookeov zakon. Minus u formuli označava smjer elastične sile koji je suprotne orijentacije od djelovanja sile koja rasteže ili pritišće oprugu.
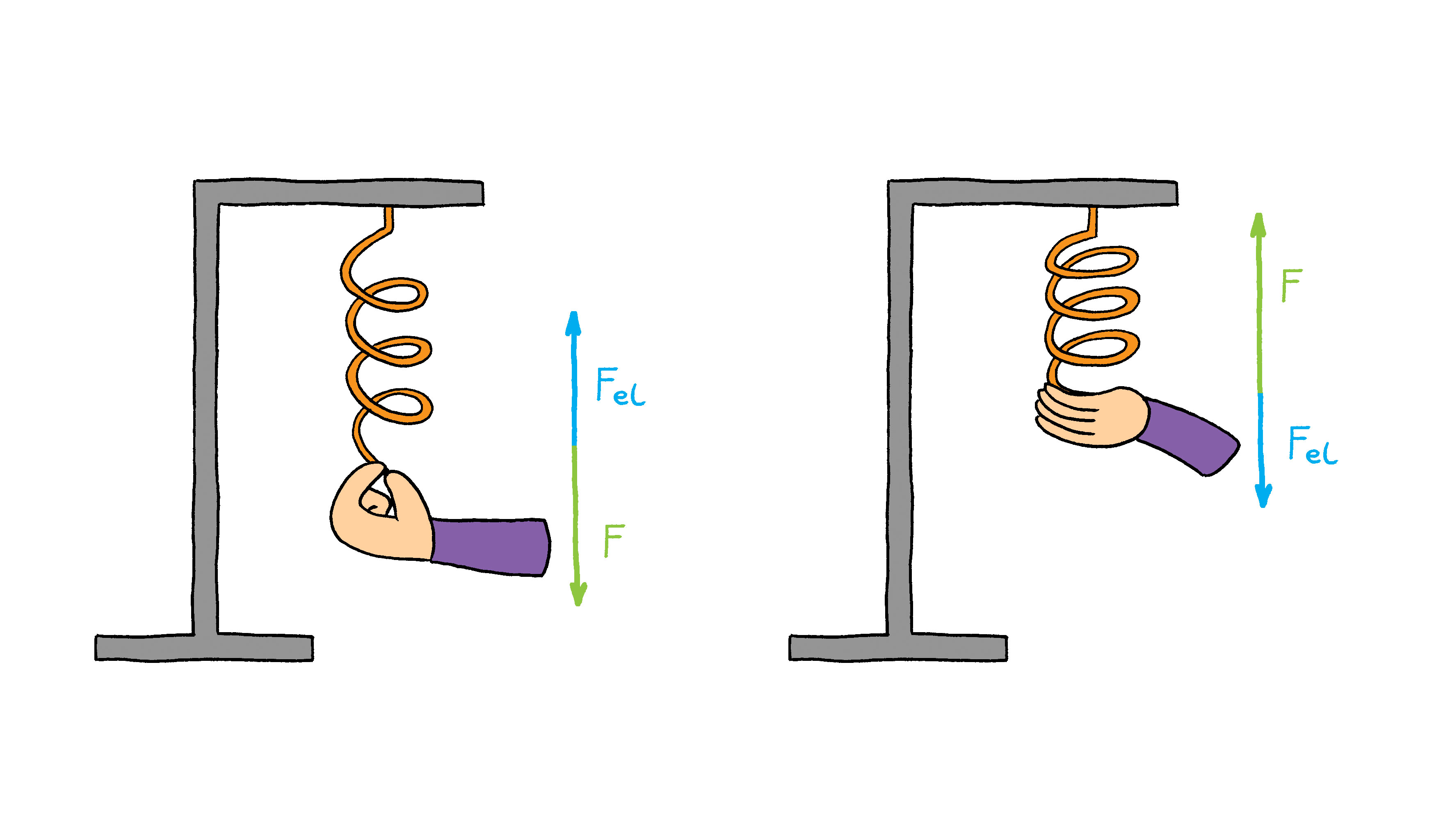
Ove dvije opruge izrađene su od različitih materijala i zbog toga je produljenje opruga različito pri djelovanju jednakim utegom.
Opruge su različite prema svojim svojstvima, a ta svojstva možemo iskazati konstantom elastičnosti opruge. Označavamo ju malim slovom i mjerimo mjernom jedinicom njutn po metru
Imaju li opruge jednaku konstantu elastičnosti?
Jesu li se opruge jednako produljile?
Koja opruga ima veću konstantu elastičnosti?
Opruga koja se više produljila ili opruga koja se manje produljila?
Primjer 1.
Na oprugu početne duljine djelovali smo silom. Očitali smo duljinu opruge i izračunali produljenje. Mjerenje smo ponovili još tri puta, mijenjajući silu, i dobili smo sljedeće podatke:
Nacrtajmo na papir graf ovisnosti produljenja opruge o sili.
Nacrtajmo na papir graf ovisnosti duljine opruge o sili.
Primjer 2.
Tamara vježba elastičnom vrpcom i rastegne ju metara. Ako je konstanta elastičnosti vrpce za vježbanje kolikom elastičnom silom vrpca djeluje na njezinu ruku?
Minus u formuli označava orijentaciju elastične sile koja je suprotna sili koja djeluje na oprugu. Kako su te dvije sile jednake, u zadatcima ne upotrebljavamo minus jer računamo samo iznos.
Daniel vozi bicikl koji ima vilicu s oprugom konstante elastičnosti Za koliko će se stisnuti opruga na biciklu ako na nju djeluje silom od
Primjer 3.
Željka želi odrediti konstantu elastičnosti opruge u dinamometru. Izmjerila je da je duljina nerastegnute opruge Kada je djelovala rukom na oprugu, očitala je silu od i izmjerila da je sada ukupna duljina opruge Kolika je konstanta elastičnosti opruge dinamometra?
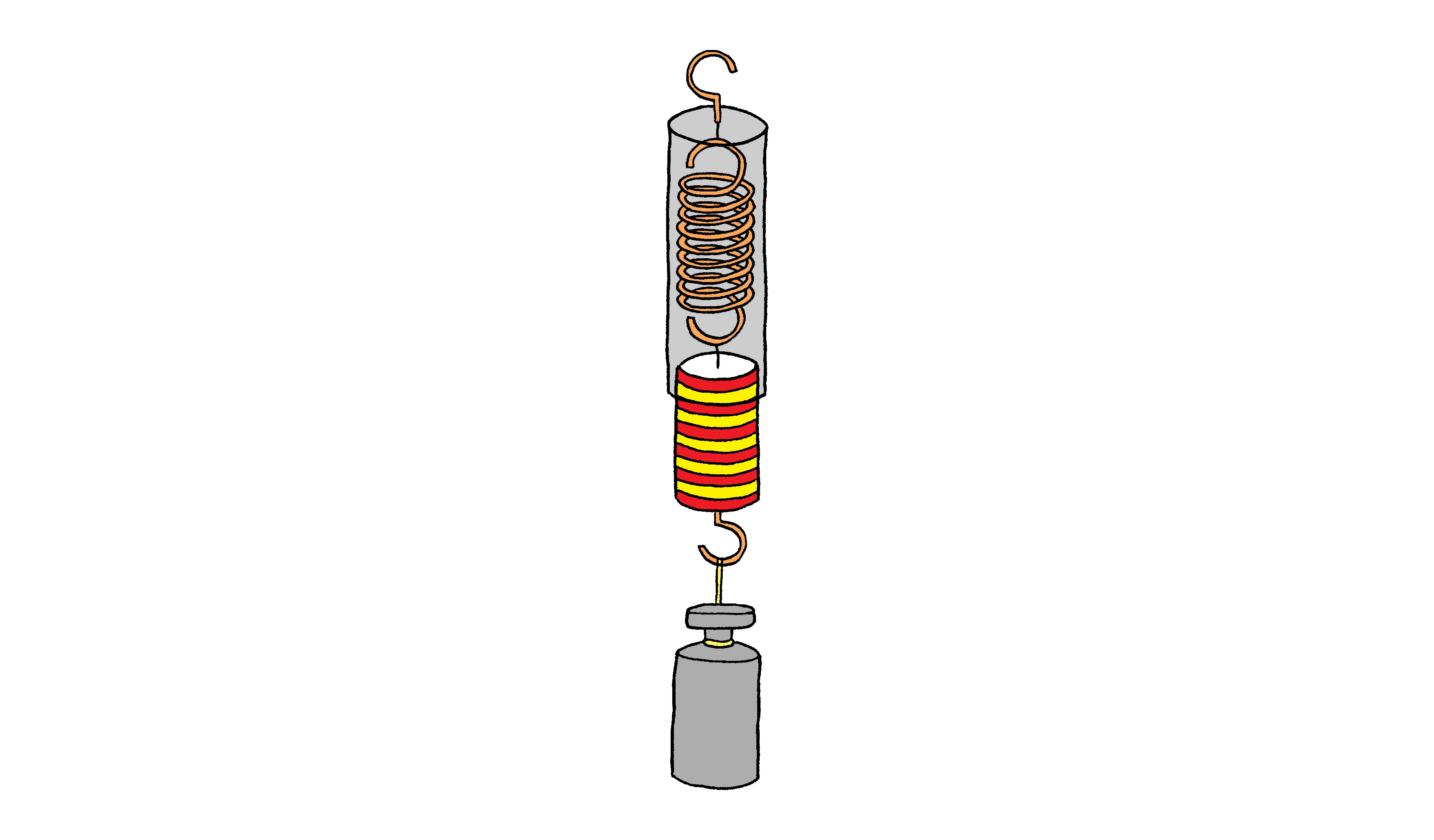
Mjerni instrument kojim mjerimo silu naziva se dinamometar. Dinamometar se sastoji od elastične opruge u kućištu i mjerne ljestvice koja pokazuje silu u njutnima. S pomoću dinamometra izravno očitavamo sile tako da na njega ovjesimo predmet ili ga vučemo po podlozi. Opruga u dinamometru rasteže se razmjerno sili kojom djelujemo. Što je sila koju mjerimo veća, to će se i opruga dinamometra više rastegnuti. Očitavanjem do koje se oznake na mjernoj ljestvici opruga rastegnula određujemo kolika je sila. Opruga će se uvijek vratiti u prvotni položaj, što omogućuje ponavljanje mjerenja.
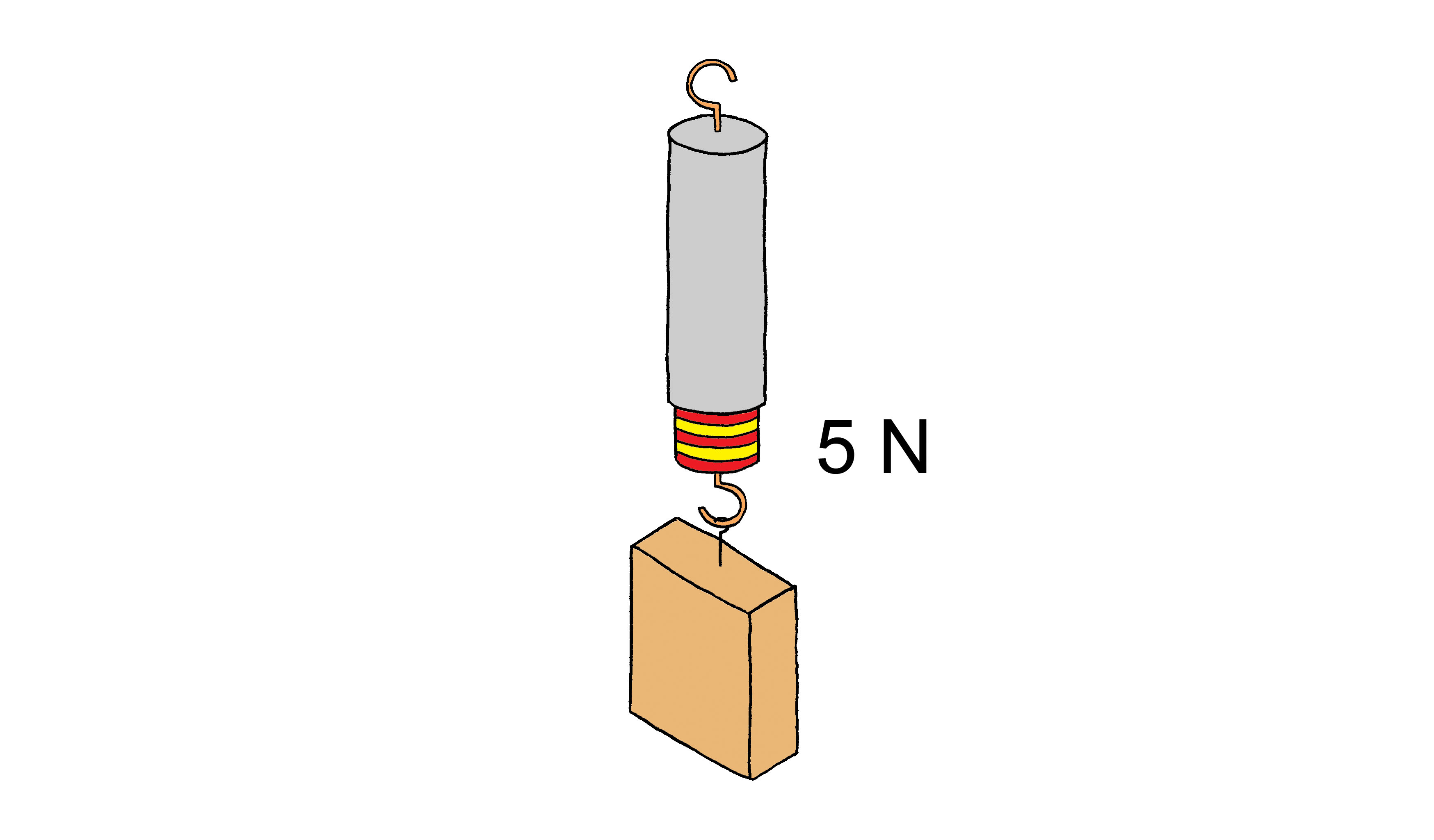
Na dinamometar smo objesili komad drveta mase i na ljestvici dinamometra očitava se vrijednost od Svaki podjeljak označava
Uvježbajmo.
Izradi dinamometar
Poznato je da uteg od isteže oprugu dinamometra silom približno . Znajući to, izradite svoj dinamometar.
Potrebno:
Postupak
Pronađite elastičnu oprugu. Izmjerite joj početnu duljinu. Objesite na nju uteg od , izmjerite duljinu opruge i izračunajte produljenje opruge. Na kartonu izradite mjernu ljestvicu. Produljenje opruge koje uzrokuje sila od prenesite na karton, podijelite tu duljinu na dijelova i dobit ćete desetinke. Oprugu i karton s mjernom ljestvicom objesite u istoj točki. Izradite kućište dinamometra.
BALON EKSPRES
Napušite balon, ali ga nemojte zavezati na vrhu nego taj vrh pridržavajte prstima. Ljepljivom vrpcom na balon zalijepite slamku. Kroz slamku provucite konac dugačak nekoliko metara i zavežite ga s jedne strane. Balon ispustite iz ruke.
Promatrajte što se događa. Razmislite i pokušajte odgovoriti zašto se balon giba? Što gura zrak iz balona van? Koja sila gura zrak iz balona van?
Primjer 4.
Elastična opruga automobila stisne se za kada na nju djelujemo silom od Za koliko će se elastična opruga stisnuti ako na nju djelujemo silom od
Elastična opruga ima početnu duljinu Domagoj ju rasteže silom od i mjeri njezinu duljinu od Kolikom silom Domagoj treba djelovati na oprugu da se ona produlji za
Robert Hooke (1635. – 1703.) britanski je fizičar, matematičar i izumitelj. Bavio se proučavanjem svojstva materijala. Ustvrdio je da produljenje tijela razmjerno ovisi o sili koja djeluje na tijelo.
Elastična sila je sila koja nastoji vratiti tijelo u prvotni oblik. Elastična sila suprotne je orijentacije od sile koja rasteže elastično tijelo. Svojstvo tijela da se nakon prestanka djelovanja sile vrati u prvotni oblik naziva se elastičnost. Svojstvo tijela da se nakon prestanka djelovanja sile ne vrati u prvotni oblik naziva se plastičnost. Elastičnu silu iskazujemo izrazom Produljenje opruge razmjerno je sili koja djeluje na oprugu. Što je sila koja djeluje na oprugu veća, to je i produljenje opruge veće.
Konstanta elastičnosti opruge razmjerna je sili koja djeluje na oprugu.
Elastična tijela vraćaju se u prvotni položaj nakon prestanka djelovanja elastične sile.
Elastična sila suprotne je orijentacije od sile koja rasteže elastično tijelo.
Instrument kojim mjerimo masu naziva se dinamometar.
Mjerna jedinica elastične sile je (njutn).
Sila koja se opire promjeni oblika tijela naziva se:
Jedan od osnovnih dijelova dinamometra koji se nalazi u kućištu je:
Kolika je vrijednost jednog podjeljka na ljestvici dinamometra ako ste izbrojili podjeljka, a na dinamometar ovjesili uteg od
Na dinamometar je ovješen uteg od Vrijednost jednog podjeljka je Koliko ćete podjeljaka izbrojiti?
Dinamometar ima ljestvicu na kojoj svaki podjeljak pokazuje . Nakon što ste ovjesili uteg na dinamometar, izbrojili ste podjeljaka. Kolikom silom djeluje uteg na dinamometar?
Kada na oprugu ovjesimo uteg od
, opruga se produlji za
Za koliko će se produljiti opruga kada su na nju ovješena dva jednaka utega?
Opruga dinamometra produljila se za kada smo na nju ovjesili jednakih utega. Za koliko će se produljiti opruga kada na nju ovjesimo samo jedan uteg?
Opruga ima početnu duljinu i nakon što smo na nju ovjesili uteg produljila se za Kolika je njezina konačna duljina?