Matematika 4 - 1.2 Računanje s kompleksnim brojevima

Zbrajanje i oduzimanje kompleksnih brojeva

Primjer 1.

Promotrimo kompleksne brojeve $z = 3 + 2 i$ i $w = 1 + 4 i .$ Kako bismo ih zbrojili? Pokušajte.

$z + w = (3 + 2 i) + (1 + 4 i) = (3 + 1) + (2 i + 4 i) = 4 + 6 i$

Zadatak 1.

Dopunite rečenicu.

Kompleksne brojeve zbrajamo tako da zbrojimo realni dio s

dijelom,

a imaginarni dio s

dijelom.

null

Zbroj kompleksnih brojeva

Zbroj kompleksnih brojeva $z = a + b i$ i $w = c + d i$ je kompleksni broj

$z + w = (a + c) + (b + d) i .$

Kako biste oduzimali kompleksne brojeve?

Zadatak 2.

Uparite zadatak i rješenje.

$(2 + 4 i) + (5 - i)$
$(9 - i) - (2 + 2 i)$
$(6 - 5 i) - (4 - 2 i)$
$(4 + i) + (- 2 + 2 i)$

null

Geometrijsko značenje zbroja i razlike kompleksnih brojeva

Zadatak 3.

Kompleksne smo brojeve prikazivali u Gaussovoj ravnini. U interakciji zbrojite zadane kompleksne brojeve $z$ i $w .$ Upišite zbroj na odgovarajuće mjesto pa točku koja se pojavi u Gaussovoj ravnini postavite na mjesto zbroja. Promotrite položaj točaka $0,$ $z,$ $w,$ $z + w .$ Što zamjećujete?

Kompleksni brojevi $0,$ $z,$ $z + w,$ $w$ prikazani su točkama koje su vrhovi paralelograma.

Prikazan je zbroj kompleksnih brojeva u Gaussovoj ravnini. — Pravilo paralelograma

Zadatak 4.

Označite sliku na kojoj su prikazani kompleksni brojevi $z$ i $z + (3 - 2 i) .$

null

Zadatak 5.

Odaberite dva kompleksna broja pa ih oduzmite. Prikažite sva tri broja u Gaussovoj ravnini. Što možete reći o njihovu međusobnom položaju?

Točke O, ze minus duplo ve, ze i duplo ve vrhovi su paralelograma. — Grafičko oduzimanje kompleksnih brojeva

Množenje kompleksnih brojeva

Primjer 2.

Pomnožimo kompleksne brojeve $z = 3 + 2 i$ i $w = 1 + 4 i .$

$(3 + 2 i) (1 + 4 i) = 3 \cdot 1 + 3 \cdot 4 i + 2 i \cdot 1 + 2 \cdot 4 i^{2} =$

$3 + 12 i + 2 i - 8 = - 5 + 14 i$

Zadatak 6.

Poredajte korake računanja.

$- 5 + 14 i$
$(3 + 2 i) \cdot (1 + 4 i)$
$3 + 12 i + 2 i + 8 i^{2}$
$3 + 12 i + 2 i - 8$

null

Kako množimo kompleksne brojeve?

Zadatak 7.

Kompleksne brojeve množimo tako da pomnožimo:

realni dio s realnim i imaginarni dio s imaginarnim dijelom

pomnožimo svaki sa svakim i primijenimo

i^{2} = - 1 .

null

Umnožak kompleksnih brojeva

Umnožak kompleksnih brojeva $z = a + b i$ i $w = c + d i$ je kompleksni broj

$z \cdot w = (a c - b d) + (a d + b c) i .$

Formulu, naravno, nećemo pamtiti nego u konkretnom zadatku množiti primjenjujući distributivnost i svojstvo imaginarne jedinice $i^{2} = - 1 .$

Zadatak 8.

Uparite zadatak i rješenje.

$(2 + 5 i) (3 - i) =$	$- 1 - 17 i$
$(5 + 2 i) (1 + 3 i) =$	$11 + 13 i$
$(2 - 5 i) (3 + i) =$	$- 1 + 17 i$
$(5 - 2 i) (1 - 3 i) =$	$11 - 13 i$

null

Zadatak 9.

Riješite zadatke.

Koliko je $(3 + 5 i) (3 - 5 i) ?$

$- 16$

$34$

null

null
Koliko je $(a + b i) (a - b i) ?$

$a^{2} + b^{2}$

$a^{2} - b^{2}$

null

null
Umnožak konjugirano kompleksnih brojeva uvijek je realan.

Da

Ne

null

null

Dijeljenje kompleksnih brojeva

Primjer 3.

Neka je $z = 1 + 7 i,$ $w = 3 + 4 i .$ Kako ćemo izračunati $\frac{z}{w} ?$ Rješenje treba zapisati u obliku $a + b i$ pa želimo postići zapis u kojemu u nazivniku nema imaginarnog dijela. Kojim brojem treba pomnožiti broj $w = 3 + 4 i$ da dobijemo realan broj? Ako nazivnik množimo nekim brojem, što treba učiniti s brojnikom da se vrijednost razlomka ne promijeni?

Broj $w = 3 + 4 i$ treba pomnožiti s konjugirano kompleksnim. Vrijednost razlomka neće se promijeniti ako brojnik i nazivnik množimo istim brojem. Pomnožimo brojnik i nazivnik s $\bar{w} = 3 - 4 i :$

$\frac{1 + 7 i}{3 + 4 i} \cdot \frac{3 - 4 i}{3 - 4 i} = \frac{3 - 4 i + 21 i + 28}{9 + 16} = \frac{31 + 17 i}{25} = \frac{31}{25} + \frac{17}{25} i .$

Kompleksne brojeve dijelimo tako da brojnik i nazivnik pomnožimo s konjugiranim nazivnikom.

$\frac{a + b i}{c + d i} = \frac{a + b i}{c + d i} \cdot \frac{c - d i}{c - d i} = \frac{(a c + b d) + i (b c - a d)}{c^{2} + d^{2}}$

Kao i u množenju kompleksnih brojeva, ni tu formulu ne pamtimo nego u konkretnom zadatku proširujemo razlomak i provodimo naznačene računske radnje.

Zadatak 10.

Uparite zadatak i rješenje.

$\frac{- 5 + 4 i}{- 1 - 3 i} =$	$\frac{9}{5} + \frac{7}{5} i$
$\frac{2 + i}{3 - i} =$	$- \frac{4}{5} + \frac{7}{5} i$
$\frac{2 + 3 i}{1 - 2 i} =$	$- \frac{7}{10} - \frac{19}{10} i$
$\frac{5 + i}{2 - i} =$	$\frac{1}{2} + \frac{1}{2} i$

null

Potencije broja i

Istražimo

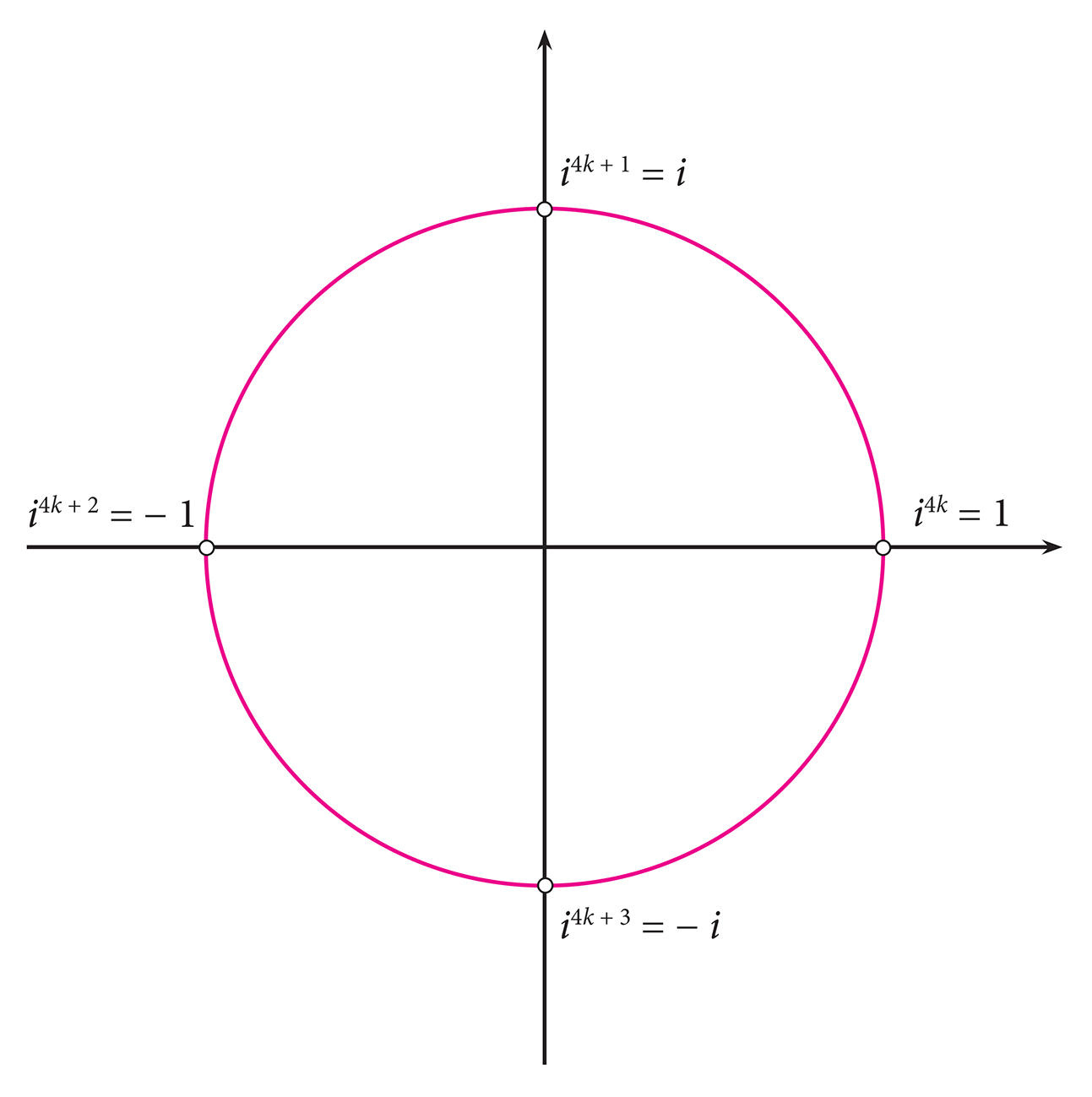
Definirali smo imaginarnu jedinicu kao broj čiji je kvadrat $- 1 .$

Izračunajte vrijednosti potencija $i^{3},$ $i^{4},$ $i^{5},$ $i^{6},$ $i^{7},$ $i^{8} .$ Uočavate li pravilnost?

Možete li predvidjeti koliko je $i^{25} ?$ A koliko je $i^{102} ?$

Opišite opće pravilo.

Vrijednosti potencija broja $i$ ciklički se ponavljaju.

Ako je eksponent djeljiv s $4,$ vrijednost je $1 .$

Ako je ostatak pri dijeljenju eksponenta s $4$ jednak $1,$ vrijednost je $i .$

Ako je ostatak pri dijeljenju eksponenta s $4$ jednak $2,$ vrijednost je $- 1 .$

Ako je ostatak pri dijeljenju eksponenta s $4$ jednak $3,$ vrijednost je $- i .$

Zadatak 11.

Uparite potenciju s njezinom vrijednosti. Broj $k$ je prirodni broj.

$i^{4 k}$	$1$
$i^{4 k + 2}$	$- i$
$i^{4 k + 3}$	$- 1$
$i^{4 k + 1}$	$i$

null

Potencije broja i smještene su na sjecištima koordinatnih osi i kružnice sa središtem u ishodištu polumjera jedan. — Potencije broja i

Zadatak 12.

$i^{7051} =$

null

null
$i^{4001} =$

null

null
$i^{2000} =$

null

null
$i^{506} =$

null

null

Kutak za znatiželjne

Izračunajte.

$i + i^{2} + i^{3} + . . . + i^{2023}$
$i \cdot i^{2} \cdot i^{3} \cdot i^{4} \cdot . . . \cdot i^{2023}$
${(1 + i)}^{2020} .$

Odgovore objasnite. Smislite sličan zadatak i podijelite ga s učenicima u razredu.

$- 1$
$1$
$- 2^{1010}$

Modul razlike kompleksnih brojeva

Modul kompleksnog broja $z$ definirali smo kao udaljenost broja $z$ prikazanog u Gaussovoj ravnini od ishodišta. Promotrimo razliku dvaju kompleksnih brojeva $z - v$ i modul te razlike. Što predstavlja broj $|z - v| ?$ Pogledajte u animaciji.

Zaključimo.

Modul razlike dvaju kompleksnih brojeva jednak je udaljenosti tih brojeva prikazanih u Gaussovoj ravnini.

Zadatak 13.

Udaljenost kompleksnih brojeva $z = 2 - 3 i$ i $w = - 3 + 5 i$ prikazanih u Gaussovoj ravnini jednaka je:

3

\sqrt{5}

\sqrt{89}

13 .

null

...i na kraju

U ovoj ste jedinici naučili zbrajati i množiti kompleksne brojeve. Potencirali ste imaginarnu jedinicu. Možemo li potencirati i druge kompleksne brojeve? Izračunajte.

${(1 + 2 i)}^{2}$
${(1 + 2 i)}^{3}$
${(1 + 2 i)}^{100}$

${(1 + 2 i)}^{2} = 1 + 4 i + 4 i^{2} = - 3 + 4 i$
${(1 + 2 i)}^{3} = 1 + 6 i + 12 i^{2} + 8 i^{3} = - 11 - 2 i$
Jasno je što bi trebalo učiniti, pomnožiti binom $1 + 2 i$ sto puta sam sa sobom. Ali taj je račun složen pa ćemo ga prepustiti računalima ili pronaći jednostavniji način.

Preostaje nam otkriti kako potenciramo bilo koji kompleksni broj na bilo koju potenciju. Pogledajte u idućim jedinicama.

Na početku...

Zbrajanje i oduzimanje kompleksnih brojeva

Primjer 1.

Zadatak 1.

Zbroj kompleksnih brojeva

Zadatak 2.

Geometrijsko značenje zbroja i razlike kompleksnih brojeva

Zadatak 3.

Zadatak 4.

Zadatak 5.

Množenje kompleksnih brojeva

Primjer 2.

Zadatak 6.

Zadatak 7.

Umnožak kompleksnih brojeva

Zadatak 8.

Zadatak 9.

Dijeljenje kompleksnih brojeva

Primjer 3.

Zadatak 10.

Potencije broja i

Istražimo

Zadatak 11.

Zadatak 12.

Kutak za znatiželjne

Modul razlike kompleksnih brojeva

Zadatak 13.

...i na kraju