Matematika 6 - Aktivnosti za samostalno učenje

Riješi, provjeri, podijeli

Za uvježbavanje kuta i trokuta predlažemo nekoliko zadataka koje možeš samostalno riješiti u bilježnicu ili u nekom interaktivnom alatu. Nakon što riješiš zadatke, usporedi svoje rješenje s rješenjima ostalih učenika.

Dvije staze u parku koje se sijeku pod šiljastim kutem. — Kut u parku

Zadatak 1.

Radnici gradskih nasada planiraju posaditi cvijeće u parku koje će biti jednako udaljeno od rubova staze na slici. Na koji način to mogu napraviti? Nacrtaj rubove staze u bilježnicu i odredi gdje bi se trebalo posaditi cvijeće.

Kako rubovi staze čine kut, cvijeće koje će biti jednako udaljeno od rubova nalazi se na simetrali kuta.

Zadatak 2.

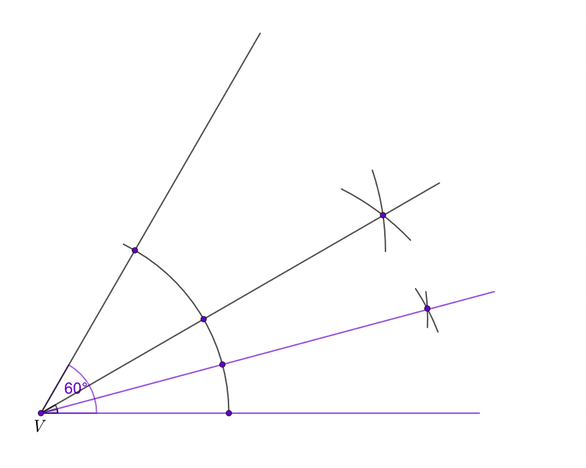
Konstruiraj kut od $60 °,$ a potom i njegovu simetralu. Označi novi kut između kraka kuta od $60 °$ i simetrale. Potom konstruiraj i njegovu simetralu. Ako ponovno označiš kut između kraka kuta od $60 °$ i nove simetrale, koja je veličina tog kuta?

Veličina tog kuta je

Razmisli!

stupnjeva.

Pomoć:

Prisjeti se kako simetrala dijeli kut na dva jednaka dijela.

null

Konstruirajući simetralu kuta od $60 °$ , taj kut prepolovljen je na dva jednaka dijela od $30 ° .$ Označimo li kut od $30 °$ i konstruiramo i njegovu simetralu, on je podijeljen na dva kuta od $15 °,$ kao što je prikazano na slici.

Kut od 60° podijeljen je simetralom na dva kuta od 30°, a kut od 30° podijeljen je simetralom na dva kuta od 15° — Simetrale 60°

Zanimljivost

O spomenutim lokacijama pročitaj na sljedećim poveznicama: Pazinska jama, Motovun Film Festival, Zvjezdarnica Višnjan.

Zadatak 3.

Učenici 6. b razreda krenuli su na izlet u Istru. Planiraju posjetiti zvjezdarnicu na Višnjanu, Pazinsku jamu i Motovunski filmski festival, a potom se ponovno vratiti pored zvjezdarnice uživati u noćnom nebu. Udaljenost od višnjanske zvjezdarnice do Motovuna je $14 km$ $,$ od Motovuna do Pazinske jame $20 km$ $,$ a od Pazinske jame do višnjanske zvjezdarnice $24 km$ $.$ Učenik Noa rekao je kako će napraviti zaista zanimljiv put nalik na trokut. Njegovi prijatelji Petar i Emanuel slažu se kako je putovanje zanimljivo, ali nisu sigurni čine li posjećena mjesta zaista trokut ili možda ipak leže na dužini. Na koji način mogu provjeriti svoje sumnje?

Označimo udaljenosti posjećenih mjesta kao

$a = 14 km$

$b = 20 km$

$c = 24 km$

Čine li posjećena mjesta trokut može se provjeriti s pomoću nejednakosti trokuta.

\begin{array}{l} a + b > c \\ a + c > b \\ b + c > a \end{array}

Pritom za dane udaljenosti vrijedi:

$\begin{array}{l} 14 + 20 > 24 \\ 14 + 24 > 20 \\ 20 + 24 > 14. \end{array}$

Kako za dane udaljenosti vrijedi pravilo nejednakosti trokuta, posjećena mjesta zaista čine trokut. Kada bi ta tri mjesta ležala na istoj dužini, tada bi udaljenost najudaljenijih mjesta bila jednaka zbroju drugih dviju udaljenosti.

Zadatak 4.

Konstruiraj trokut iz prethodnog zadatka prema poučku o sukladnosti SSS. Navedene stranice prikaži u centimetrima, a potom složi korake konstrukcije.

Povlačenjem miša poredaj korake konstrukcije.

Prije konstrukcije potrebno je analizirati zadatak i napraviti skicu.
U šestar unijeti $20 cm,$ ubosti u točku koja predstavlja Motovun i povući luk koji siječe već povučeni luk.
Na drugom kraju dužine označiti točku koja predstavlja Motovun.
Dužinama spojiti točke.
U šestar unijeti $24 cm,$ ubosti u točku koja predstavlja Višnjan i povući luk.
Raspraviti na koje se sve načine mogla provesti konstrukcija.
Iz označene točke povući dužinu duljine $14 cm .$
Na sjecištu lukova označiti točku koja predstavlja Pazinsku jamu.
Označiti točku koja predstavlja zvjezdarnicu na Višnjanu.

Pomoć:

Prisjeti se SSS konstrukcije trokuta.

null

Zadatak 5.

Koliku su udaljenost prešli učenici od Zvjezdarnice Višnjan do Motovuna i Pazinske jame i pri povratku nazad u zvjezdarnicu?

Udaljenost koju su prešli jednaka je opsegu trokuta koji čine točke koje predstavljaju spomenuta mjesta, a to je:

$o = a + b + c = 14 + 20 + 24 = 58 km .$

Obilazeći spomenuta mjesta učenici su prešli $58 km .$

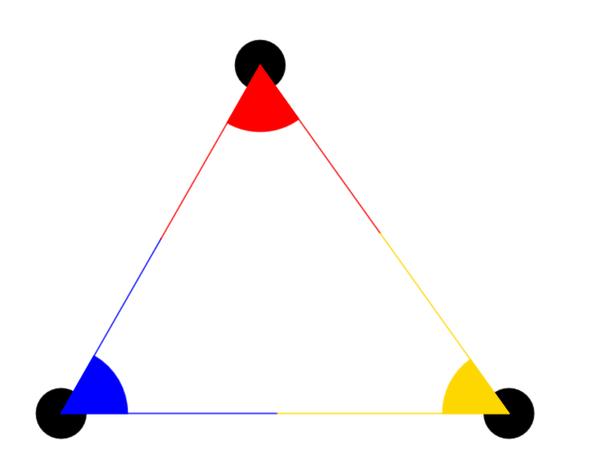
Tri reflektora, plavi, crveni i žuti bacaju svjetlo na pozornicu. Pri tome čine trokut. — Reflektori

Zadatak 6.

Na koncertnoj pozornici smješteni su reflektori. Rock-grupa koja će nastupati zahtijeva da oni čine trokut. Plavi reflektor baca snop svjetlosti koji se širi pod kutom od $57 °,$ a crveni pod kutom od $76 °,$ kao što je prikazano na slici. Pod kojim kutom žuti reflektor baca snop svjetlosti ako reflektori čine trokut?

Žuti reflektor mora bacati snop svjetlosti pod kutom od

Razmisli!

stupnjeva

kako bi reflektori činili trokut.

Pomoć:

Zbroj kutova u trokutu je $180 ° .$

null

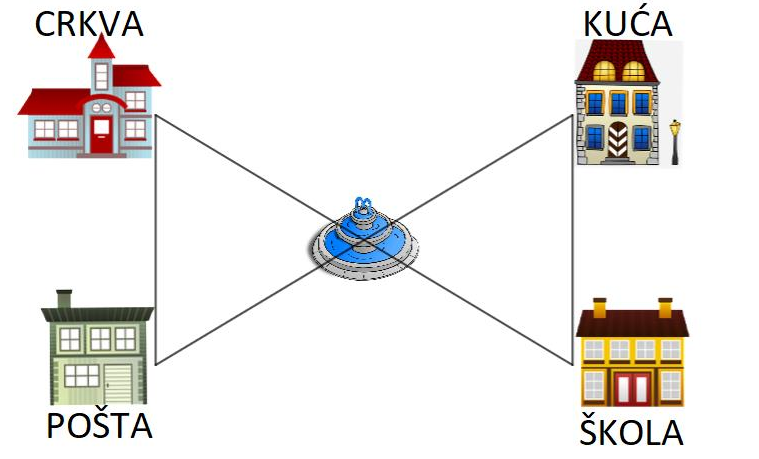
Slika prikazuje kuću, pored nje školu i ispred njih fontanu. S druge strane fontane su jedna ispod druge crkva i pošta. — Udaljenost od kuće do škole

Zadatak 7.

Djevojčica Luna nacrtala je dvije ulice svoga mjesta koje se sijeku na trgu. Primijetila je kako su crkva i škola jednako udaljene od trga, baš kao i njezina kuća i pošta, kao što je vidljivo na slici. Isto tako, ulica u kojoj su njezina kuća i škola paralelna je s ulicom u kojoj su crkva i pošta. Koliko je udaljena njezina kuća od škole ako je crkva od pošte udaljena $150 m ?$

Udaljenost kuće i škole je

Razmisli!

m .

Pomoć:

Neka crkva, trg i pošta čine jedan trokut, a trg, kuća i škola drugi trokut. Ta dva trokuta su sukladna, prema poučku o sukladnosti trokuta, kao što je vidljivo na slici.

null

Pri rješavanju koristio se

poučak

o sukladnosti trokuta.

Pomoć:

Dana su dva para jednakih udaljenosti (od crkve do trga i od trga do škole te od kuće do trga i od trga do pošte). Primijeti kako su i kutovi pod kojim se sijeku ulice jednaki (vršni kutovi).

null

Zadatak 8.

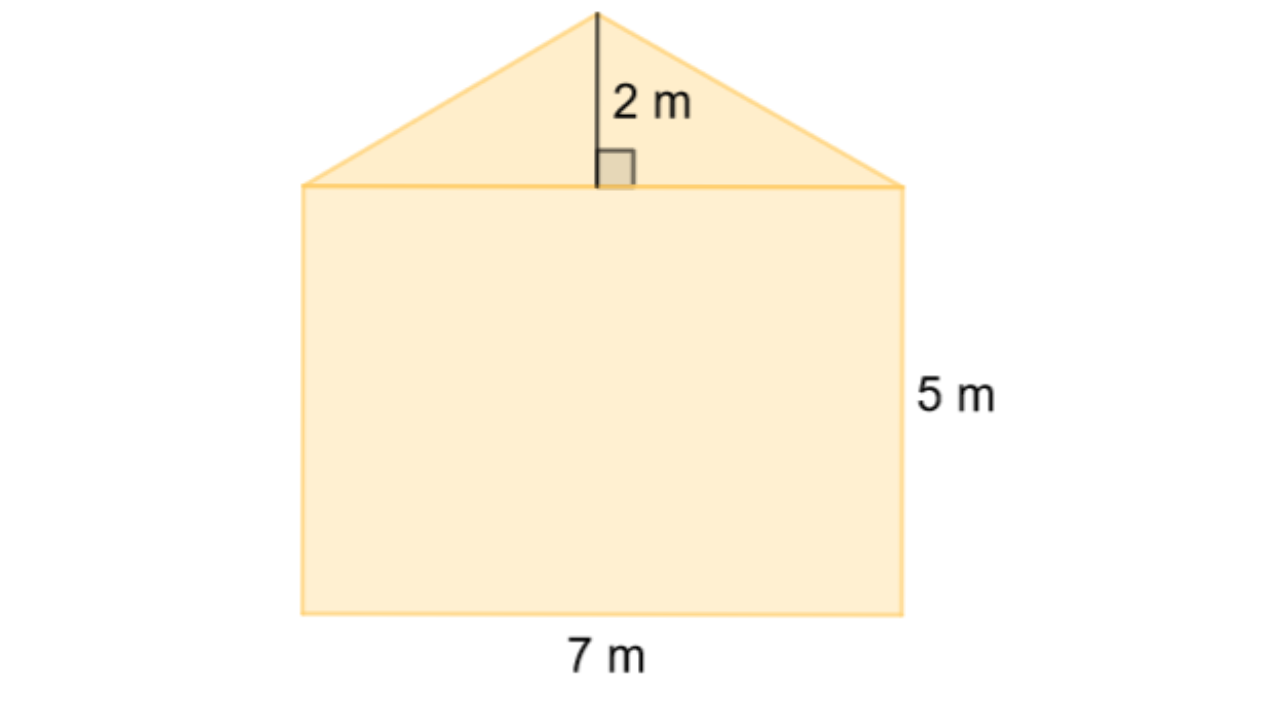
Ličioci Ivan i Dario planiraju obojiti jednu stranu kuće kao na slici.

a. Ako potroše $1.5$ litru boje za $1 m^{2}$ fasade, koliko će im boje trebati za ovaj posao?

b. Ako $1$ litra boje košta $50 kn$ , koliki će iznos morati platiti za svu boju koju će potrošiti ličeći fasadu na jednoj strani kuće?

a. Stranu kuće koju ličioci boje podijeli na dva geometrijska lika kojima znaš izračunati površinu: trokut i kvadrat. Vrijedi:

$p_{1} = \frac{7 \cdot 2}{2} = 7 m^{2}$

$p_{2} = 7 \cdot 5 = 35 m^{2}$

$p = p_{1} + p_{2} = 7 + 35 = 42 m^{2}$

Količina boje koja je potrebna za ličenje fasade na spomenutoj strani kuće je

$42 \cdot 1.5 = 63$ litre.

b. Iznos koji moraju platiti za svu boju koju će potrošiti ličeći fasadu jedne strane kuće je

$63 \cdot 50 = 3150 kn .$

2.7 Aktivnosti za samostalno učenje

Na početku...

Riješi, provjeri, podijeli

Zadatak 1.

Zadatak 2.

Zanimljivost

Zadatak 3.

Zadatak 4.

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Projekt

Kutak za znatiželjne

...i na kraju