Matematika 7 - 7.7 Površina mnogokuta

Trokut

Površina jednaka je polovici duljina njegove stranice i njoj pripadajuće visine.

Zadatak 1.

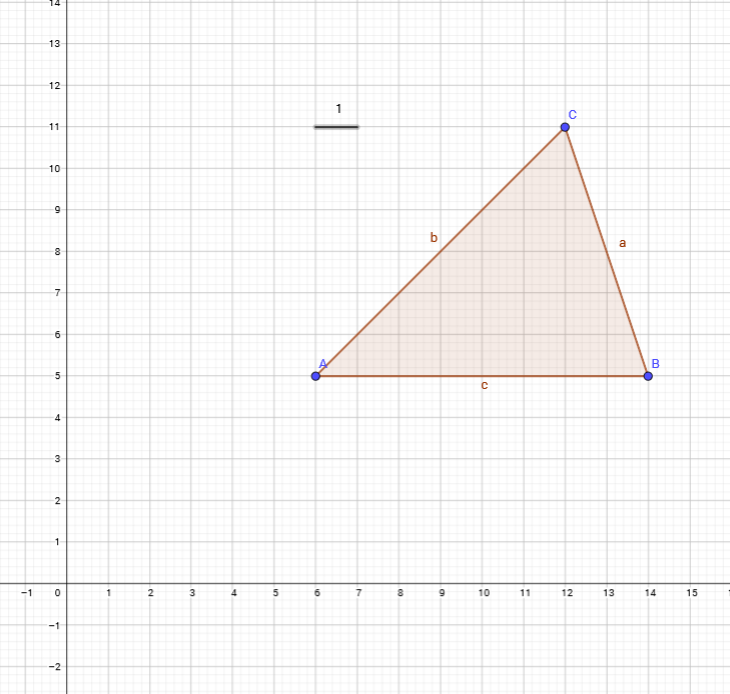
Na slici je nacrtan trokut u pravokutnom koordinatnom sustavu s koordinatama vrhova A(6,5), B(14,5) i C(12,11).

Izračunajte površinu trokuta sa slike.

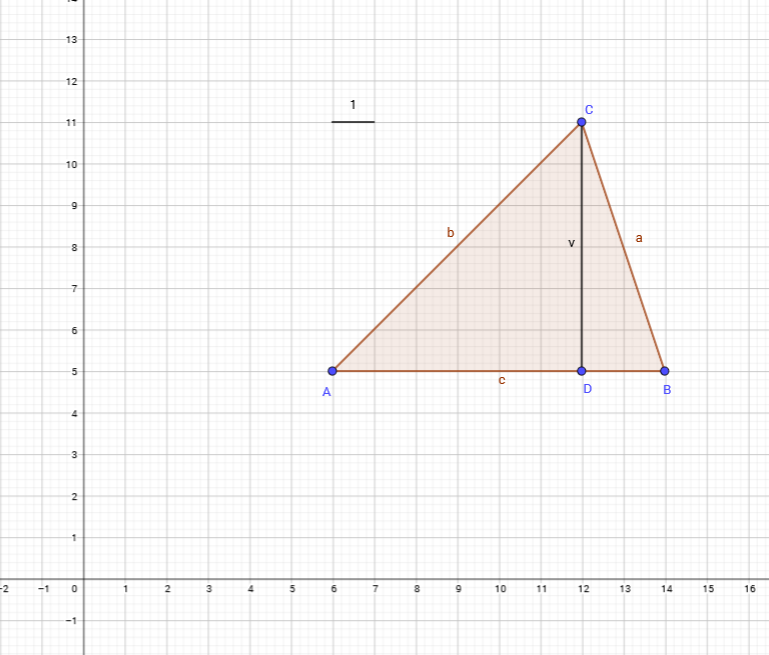
Na slici je prikazan trokut i njemu pripadajuća visina na stranicu c.

Površina trokuta jednaka je polovici umnoška duljine stranice i njoj pripadajuće visine.

Na zadanoj slici vidljivo je da je duljina stranice $c = 8,$ a njoj pripadajuće visine $v = 6 .$

Stoga je $P = \frac{8 \cdot 6}{2} = 24$ kvadratnih jedinica.

Praktična vježba

S pomoću računalnog programa dinamičke geometrije nacrtajte trokut $A B C .$ Uporabom odgovarajućih programskih alata nacrtajte visinu trokuta spuštenu iz vrha $C .$ Izmjerite i zapišite duljine stranice $c$ i njoj pripadajuće visine. Izračunajte površinu dobivenog trokuta.

Četverokut

Kolekcija zadataka 1

Zadatak 2.

Spojite odgovarajuće parove.

Paralelogram	$P = a \cdot b$
Trapez	$P = a \cdot a$
Kvadrat	$P = a \cdot v_{a}$
Romb	$P = \frac{e \cdot f}{2}$
Pravokutnik	$P = \frac{(a + c) \cdot v}{2}$

Pomoć:

Spojite odgovarajući četverokut i formulu za izračunavanje njegove površine.

Zadatak 3.

Izračunajte površine četverokuta na slici.

Romb	$P = 21 {cm}^{2}$
Paralelogram	$P = 12 {cm}^{2}$
Trapez	$P = 37.5 {cm}^{2}$

Pomoć:

$P = \frac{e \cdot f}{2}$ površina romba

$P = a \cdot v$ površina paralelograma

$P = \frac{(a + c) \cdot v}{2}$ površina trapeza

null

Zatvori

Površine mnogokuta izračunavamo tako da mnogokut podijelimo na likove čije površine znamo izračunati.

Primjer 1.

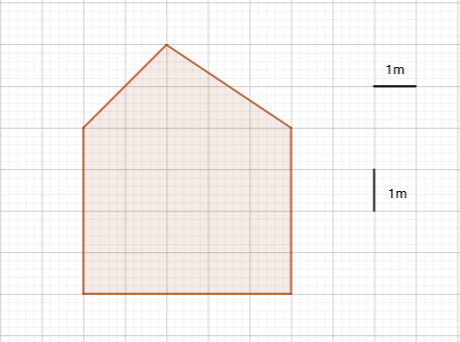
Izračunajmo površinu peterokuta na slici.

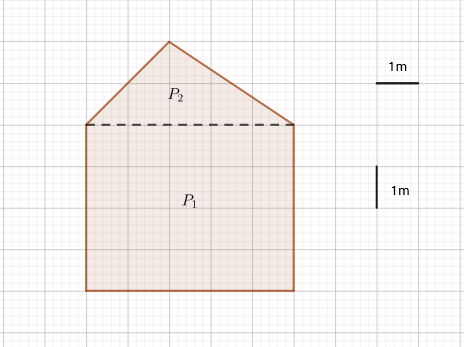
Na slici je nacrtan peterokut koji je razdijeljen na jedan pravokutnik i jedan trokut.

Podijelimo peterokut na pravokutnik i trokut.

Površinu pravokutnika označit ćemo s $P_{1},$ duljine njegovih stranica su $5 m$ i $4 m .$

Zato imamo: $P_{1} = 5 m \cdot 4 m = 20 m^{2} .$

Površinu trokuta označit ćemo s $P_{2}$ ; duljina stranice je $5 m$ i njoj pripadajuće visine $2 m .$

Zato imamo $P_{2} = \frac{5 m \cdot 2 m}{2} = 5 m^{2} .$

Površina peterokuta sa slike jednaka je zbroju površina $P_{1}$ i $P_{2} .$

$P = P_{1} + P_{2}$

$P = 20 {cm}^{2} + 5 {cm}^{2} = 25 {cm}^{2} .$

Zadatak 4.

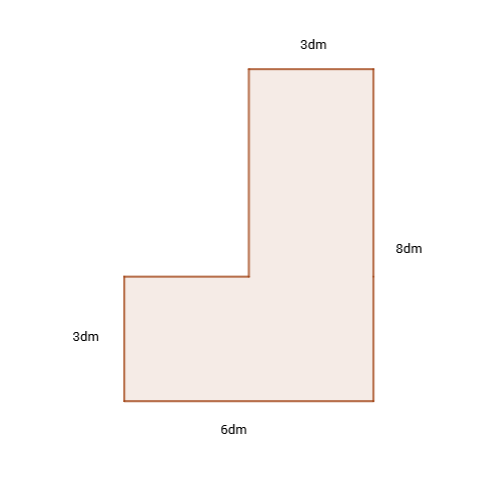
Izračunajte površinu mnogokuta sa slike.

Na slici je prikazan mnogokut sastavljen od jednog kvadrata duljine stranice 3dm i pravokutnika duljina stranica 3dm i 8dm.

Podijelite mnogokut na kvadrat duljine stranice $3 dm$ i pravokutnik duljina stranica $8 dm$ i $3 dm .$

$P = 33 {dm}^{2}$

Primjer 2.

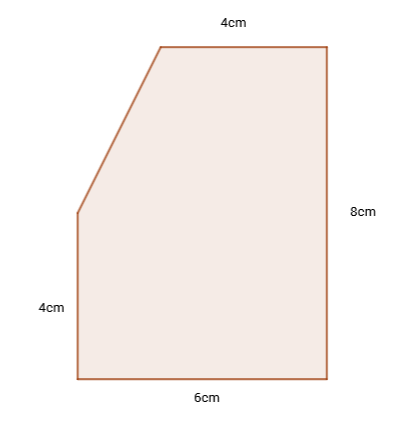
Izračunajmo površinu mnogokuta sa slike.

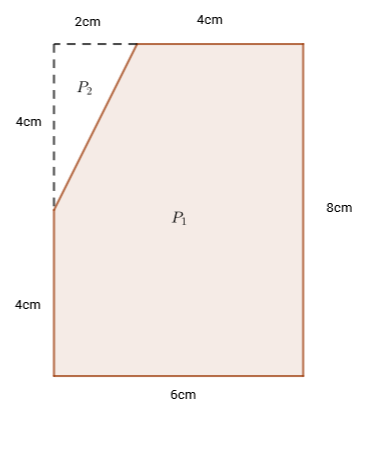
Na slici je prikazan peterokut nadopunjen pravokutnim trokutom.

Dopunimo mnogokut pravokutnim trokutom tako da dobijemo pravokutnik.

Površinu pravokutnika označit ćemo s $P_{1},$ a duljine stranica su $6 cm$ i $8 cm .$

Zato imamo:

$P_{1} = 6 c m \cdot 8 c m = 48 c m^{2} .$

Površinu pravokutnog trokuta označit ćemo s $P_{2},$ a duljine kateta su $2 cm$ i $4 cm .$

Zato imamo: $P_{2} = \frac{2 c m \cdot 4 c m}{2} = 4 c m^{2} .$

$P = P_{1} - P_{2}$

$P = 48 c m^{2} - 4 c m^{2} = 44 c m^{2} .$

Tlocrt Ivanova stana prikazan je na slici. Površina stana je:

80 m^{2}

Dopunite crtež do pravokutnika.

84 m^{2}

Dopunite crtež do pravokutnika.

72 m^{2}

Pomoć:

Na slici je prikazan osmerokut koji je nadopunjen do pravokutnika.

Postupak:

$P = P_{1} - P_{2} - P_{3}$

Površina pravilnih mnogokuta

Površina pravilnog mnogokuta s $n$ stranica jednaka je umnošku broja $n$ i površine karakterističnog trokuta

$P = n \cdot \frac{a \cdot ρ}{2}$

gdje je $a$ duljina stranice pravilnog mnogokuta, a $ρ$ duljina polumjera upisane kružnice.

Primjer 3.

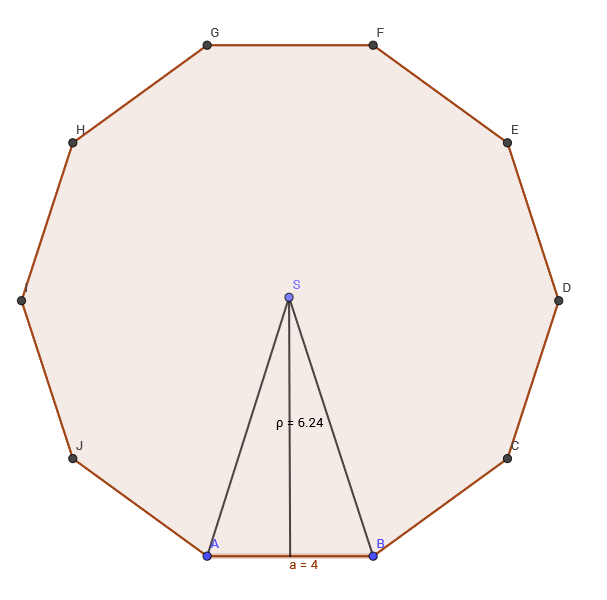
Izračunajmo površinu pravilnog mnogokuta sa slike.

Iz slike možemo zaključiti da se radi o pravilnom deseterokutu, da je duljina jedne stranice $4,$ a duljina polumjera upisane kružnice $6.24 .$

Zato je površina pravilnog deseterokuta $P = 10 \cdot \frac{4 \cdot 6.24}{2} = 124.8$ kvadratnih jedinica.

Zadatak 5.

Izračunajte površinu pravilnog mnogokuta kojemu je duljina jedne stranice $3.5 cm,$ duljina polumjera upisane kružnice je $6.5 cm$ i zbroj veličina unutarnjih kutova $1 800^{\circ} .$

$K_{n} = 1 800^{\circ}$

$a = 3.5 c m$

$ρ = 6.5 c m$

$(n - 2) \cdot 180^{\circ} = 1 800^{\circ} \Rightarrow n = 12$

$P = 12 \cdot \frac{3.5 c m \cdot 6.5 c m}{2} = 136.5 c m^{2} .$

...i na kraju

Ponovimo:

površinu mnogokuta izračunavamo tako da mnogokut podijelimo na likove kojima znamo izračunati površinu
površinu pravilnog mnogokuta možemo izračunati ako znamo duljinu polumjera upisane kružnice i duljinu stranice.

Kolekcija zadataka 2

Da bismo izračunali površinu romba, dovoljno je da znamo duljinu njegovih dijagonala.

Da.

Ne.
$P = \frac{e \cdot f}{2}$

Pomoć:

$P = \frac{e \cdot f}{2}$
Površina lika sa slike je:

$23 m^{2}$

$32 m^{2}$

$40 m^{2}$

Pomoć:

Podijeli zadani lik na manje likove kojima znaš izračunati površinu. Na slici je prikazan jedan od načina kako to možeš napraviti.

Postupak:

$P = P_{1} + P_{2} + P_{3} + P_{4}$

Spojite odgovarajuće parove.

$P = \frac{a \cdot b}{2}$
$P = a \cdot b$
$P = \frac{c \cdot v_{c}}{2}$
$P = \frac{(a + c) \cdot v}{2}$

Zatvori

7.7 Površina mnogokuta

Na početku...

Trokut

Zadatak 1.

Praktična vježba

Četverokut

Kolekcija zadataka 1

Zadatak 2.

Zadatak 3.

Zadatak 4.

Površina pravilnih mnogokuta

Zadatak 5.

...i na kraju

Kolekcija zadataka 2

7.8 Mnogokuti u svakodnevnom životu