Matematika 7 - Aktivnosti za samostalno učenje

Kako biste što uspješnije usvojili znanja o mnogokutima, predlažemo vam nekoliko zadataka koje možete samostalno riješiti u bilježnicu ili u nekoj aplikaciji za dinamičnu geometriju, poput GeoGebre. Posljednji zadaci predviđeni su za one koji žele znati više i spremni su na složenije matematičke izazove, ali to ne znači da ih svi ne možete barem pokušati riješiti. Nakon što riješite zadatke, usporedite svoja rješenja s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili ih zamolite da oni svoje znanje podijele s vama i pomognu vam pri rješavanju onih zadataka koji su vam bili zahtjevniji.

Kolekcija zadataka 1

Zadatak 1.

Pridružite oznaci odgovarajući opis.

$d_{n}$	zbroj unutarnjih kutova
$D_{n}$	broj dijagonala iz jednog vrha
$n$	broj vrhova
$K_{n}$	ukupni broj dijagonala

Pomoć:

Potražite pomoć u jedinici Osnovno o mnogokutima.

null

Zadatak 2.

Broj vrhova nekog mnogokuta uvijek je broj dijagonala iz jednog vrha tog mnogokuta.

Pomoć:

$d_{n} = n - 3$

null

Zadatak 3.

Kako se zove $n$ -terokut koji ima trinaest stranica?

Pomoć:

Broj stranica jednak je broju kutova.

Postupak:

Trinaesterokut
Kako zovemo stranice mnogokuta koje imaju zajedničku onu točku koja je vrh mnogokuta?

nesusjedne stranice

vršne stranice

susjedne stranice
Dopunite sljedeće rečenice.
Ukupan broj dijagonala $n$ -terokuta računamo kao

.

Veličinu unutarnjeg kuta pravilnog $n$ -terokuta računamo kao

.

Zbroj veličina svih unutarnjih kutova $n$ -terokuta računamo kao:

.

$K_{n} = (n - 2) \cdot 180 °$

$α_{n} = \frac{(n - 2) \cdot 180 °}{n}$

$D_{n} = \frac{n \cdot (n - 3)}{2}$

Zadatak 4.

Skicirajte mnogokut koji ima jedanaest unutarnjih kutova i dopunite sljedeće rečenice.
Iz jednog vrha zadanog mnogokuta može se nacrtati najviše dijagonala, a ukupno čak dijagonale. Zbroj veličina svih njegovih unutarnjih kutova iznosi

° .

Pomoć:

Pokušajte se prisjetiti kako se izračunava broj dijagonala iz jednog vrha, ukupni broj dijagonala i zbroj veličina unutarnjih kutova mnogokuta.

Postupak:

$d = n - 3 = 11 - 3 = 8$

$D_{n} = \frac{n \cdot (n - 3)}{2} = 44$

$K_{n} = (n - 2) \cdot 180 ° = 1620 °$

Zatvori

Kolekcija zadataka 2

Zadatak 5.

Spojite odgovarajuće parove (tako da element za povlačenje dovedete u donji desni kut odgovarajućeg pravokutnika u boji).

Slika sadrži opise: zbroj veličina unutarnjih kutova, zbroj veličina svih vanjskih kutova, zbroj veličina unutarnjeg i pripadnog mu vanjskog kuta.

$(n - 2) \cdot 180 °$

$360 °$

$180 °$

Pomoć:

Od navedenih, samo zbroj veličina unutarnjih kutova ovisi o broju stranica mnogokuta.

null

Zadatak 6.

Središnji kut pravilnoga osmerokuta ima veličinu

°,

a veličina njegova unutarnjega kuta iznosi

° .

Pomoć:

Središnji kut pravilnog osmerokuta je osmina punoga kuta. Veličina unutarnjeg kuta je osmina zbroja veličina svih unutarnjih kutova osmerokuta.

Postupak:

$β_{8} = \frac{360 °}{8} = 45 °$

Zadatak 7.

Konstruirajte kvadrat koji je upisan u kružnicu polumjera $3.5 cm .$

Koraci konstrukcije prikazani su u sljedećoj interakciji.

Zadatak 8.

Konstruirajte pravilni osmerokut kojemu je opisana kružnica duljine polumjera $3.5 cm .$ Možete, ako želite, konstrukciju izvesti koristeći se kvadratom konstruiranim u prethodnom zadatku.

Koraci konstrukcije prikazani su u sljedećoj interakciji.

Zatvori

Kolekcija zadataka 3

Zadatak 9.

Konstruirajte pravilni šesterokut kojemu je opisana kružnica polumjera $3 cm .$

Koraci konstrukcije prikazani su u sljedećoj interakciji.

Zadatak 10.

Konstruirajte jednakostranični trokut koji je upisan u kružnicu promjera $5 cm .$

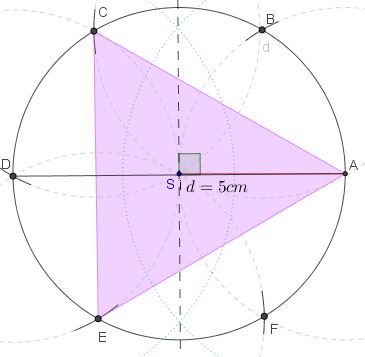
Slika prikazuje jednakostraničan trokut upisan u kružnicu

Da bismo konstruirali traženi trokut, potrebno je najprije zadanome promjeru, konstrukcijom simetrale dužine, konstruirati polovište koje će biti središte $S$ tražene kružnice. Dalje pratimo korake konstrukcije pravilnog šesterokuta (prethodni zadatak) do posljednjeg koraka. Vrhovi $A,$ $C$ i $E$ ili $B,$ $D$ i $F$ su vrhovi jednakostraničnog trokuta.

Zadatak 11.

Ako površina karakterističnog trokuta pravilnog dvanaesterokuta iznosi $4.9 {cm}^{2},$ kolika je površina tog mnogokuta?

93.1 {cm}^{2}

58.8 {cm}^{2}

16.9 {cm}^{2}

Pomoć:

Pravilni dvanaesterokut sastoji se od dvanaest sukladnih karakterističnih trokuta.

Postupak:

$P = 12 \cdot 4.9 {cm}^{2} = 58.8 {cm}^{2}$

Zadatak 12.

Ako opseg pravilnog mnogokuta iznosi $37.8 cm,$ a duljina jedne njegove stranice je $4.2 cm,$ izračunajte veličinu pripadnog unutarnjeg kuta.

Osmislite plan rješavanja, a zatim provjerite točnost rješavajući zadatak a).

Odredite točan redoslijed radnji kako biste izračunali traženu veličinu kuta.
Izračunajmo veličinu kuta uz osnovicu.

Izračunajmo broj stranica pravilnog mnogokuta.

Izračunajmo veličinu središnjeg kuta.
Pomoć:

Osim na ovaj način, do rješenja se može doći i izračunavanjem zbroja veličina svih unutarnjih kutova pa dijeljenjem s brojem kutova.
Zadani pravilni mnogokut ima stranica.

Pomoć:

Traženi mnogokut je deveterokut jer je $n = \frac{o p s e g m n o g o k u t a}{d u l j i n a s t r a n i c e} .$
Istaknutim kutovima karakterističnog trokuta pravilnog deveterokuta pridruži odgovarajuće veličine kutova.

$140 °$

$40 °$

$70 °$

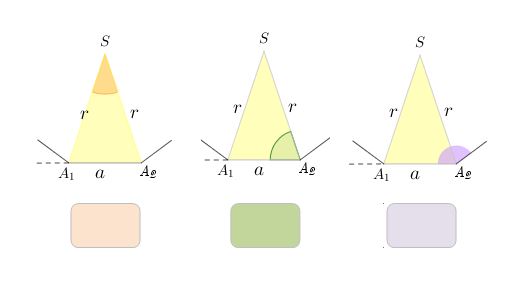
Pomoć:

Središnji kut pravilnog deveterokuta je devetina punoga kuta, tj. $β_{9} = 40 °$

Postupak:

$α_{9} = \frac{K_{9}}{9} = 140 °$

Zatvori

Kolekcija zadataka 4

Zadatak 13.

Nacrtajte pravilni deveterokut čija stranica ima duljinu $25 mm .$

Koraci su prikazani u sljedećoj interakciji.

Zadatak 14.

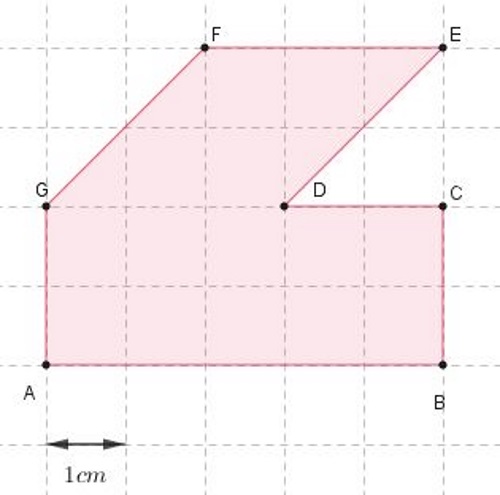
Slika prikazuje mnogokut u kvadratnoj mreži.

Izračunajte površinu mnogokuta sa slike na barem dva načina.

Slike prikazuju isti mnogokut kome na dva načina računamo površinu (podjela na poznate likove ili dopuna do pravokutnika)

Na primjer:

Dva su osnovna načina na koje možemo odrediti površinu zadanoga lika. Prvi, rastavljanjem zadanog mnogokuta na geometrijske likove čiju površinu znamo izračunati, i drugi, dopuniti zadani lik do pravokutnika kojemu možemo izračunati površinu te oduzeti površine koje su suvišne.

Zadatak 15.

Koliko dijagonala iz jednog vrha ima mnogokut kojemu zbroj veličina svih unutarnjih kutova iznosi $3 420 ° ?$

21

Odgovor nije točan. Dobiveno rješenje je broj vrhova zadanog mnogokuta.

18

19

Odgovor nije točan. Devetnaest je broj trokuta nastalih crtanjem dijagonala iz jednog vrha.

Pomoć:

Podijelimo li $K_{n}$ sa $180 °,$ dobit ćemo broj trokuta nastalih crtanjem dijagonala iz jednog vrha mnogokuta, što je za dva manji broj od broja vrhova mnogokuta. Prisjetite se povezanosti broja vrhova i broja dijagonala iz jednog vrha mnogokuta.

Postupak:

$n - 2 = 19$

n = 21

d_{21} = 18

Zadatak 16.

Mnogokut kojemu se može nacrtati ukupno

275

dijagonala ima vrhova.

Pomoć:

Iz $\frac{n \cdot (n - 3)}{2} = 275$ slijedi da je $n \cdot (n - 3) = 550 .$ Sada je potrebno pronaći brojeve čiji je umnožak $550,$ a jedan od njih je za tri veći od drugoga.

Zatvori

Kutak za znatiželjne

Kolekcija zadataka 5

Zadatak 17.

Ako se nekom mnogokutu broj stranica poveća za četiri, zbroj veličina njegovih unutarnjih kutova će se utrostručiti. Koji je to mnogokut?

Zadatak 18.

Postoji li peterokut koji ima četiri prava kuta? Kako biste obrazložili svoj odgovor?

Da.

Ne.

Pomoć:

Izračunajte zbroj veličina unutarnjih kutova peterokuta i usporedite ga s poznatim podacima o zadanom liku.

Postupak:

Ako je $K_{5} = 3 \cdot 180 ° = 540 °,$ a četiri prava kuta zajedno iznose $360 °,$ preostali kut mora imati veličinu ispruženog kuta, što nije moguće.

Zadatak 19.

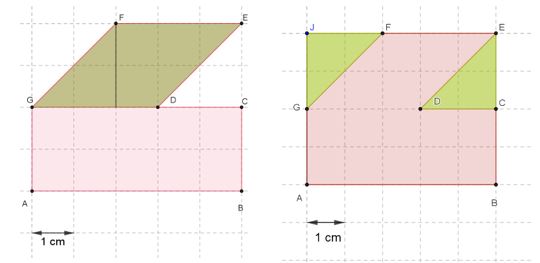
Odredite izraze za opseg i površinu lika sa slike.

Prebrojimo dužine duljine $3 a$ kojima je omeđen zadani lik. Ima $32$ takve dužine pa opseg lika možemo izraziti kao $O = 32 \cdot 3 a = 96 a .$

Da bismo izrazili površinu, treba prebrojiti kvadratiće - ima ih $27 .$ Budući da jedan kvadratić ima površinu $P_{1} = 3 a \cdot 3 a = 9 \cdot a \cdot a,$ ukupna će površina biti $P = 27 \cdot 9 \cdot a \cdot a = 243 \cdot a \cdot a .$

Zadatak 20.

Slika prikazuje hol sa stolom u obliku osmerokuta.

U predvorju jedne osječke škole stolovi su složeni u obliku "vijenca" pravilnog osmerokuta, kako prikazuje fotografija. Vijenac čini osam jednakih stolova oblika jednakokračnog trapeza. Usporedne rubove stola, čije su dimenzije $1.6 m$ i $96 cm,$ trebalo bi zaštititi posebnom ljepljivom trakom.

Koliko je trake potrebno kupiti ako se u predvorju nalaze tri "vijenca" stolova?

$20.48 m$

$780.8 m$
Prije računanja treba uskladiti mjerne jedinice.

$61.44 m$

Pomoć:

Količina potrebne trake predstavlja unutarnji i vanjski opseg pravilnog osmerokuta. Ne zaboravite prije računanja uskladiti mjerne jedinice. Nakon što izračunate količinu trake potrebne za jedan "vijenac" stolova, ne zaboravite da su u predvorju tri vijenca.

Postupak:
Traku treba lijepiti na rub velikog pravilnog osmerokuta ( $O_{v} = 1.6 m \cdot 8 = 12.8 m$ ) te na rub manjeg pravilnog osmerokuta ( $O_{m} = 0.96 m \cdot 8 = 7.68 m$ ). Ukupno je to $20.48 m$ trake za jedan vijenac. Kako biste mogli zapisati račun, želite li primijeniti distributivnost?
Ako jedno pakiranje trake sadrži $25 m,$ potrebno je kupiti pakiranja.

Postupak:

Budući da je $25 m \cdot 2 = 50 m,$ to je premalo, a $25 m \cdot 3 = 75 m$ bit će dovoljno. Dakle, potrebna su tri pakiranja trake.

Zadatak 21.

Pokušajte konstruirati kvadrat i pravilni osmerokut upisan u kružnicu uz pomoć GeoGebre.

Zatvori

Projekt

Odaberite jednu prostoriju u svojem domu koju biste željeli renovirati. Odaberite materijale potrebne za obnovu, napravite izračun količine i približan trošak. Ne zaboravite u trošak uračunati i cijenu rada.

Aktivnosti za samostalno učenje

Na početku...

Riješite, provjerite, podijelite

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zadatak 3.

Zadatak 4.

Kolekcija zadataka 2

Zadatak 5.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Kolekcija zadataka 3

Zadatak 9.

Zadatak 10.

Zadatak 11.

Zadatak 12.

Kolekcija zadataka 4

Zadatak 13.

Zadatak 14.

Zadatak 15.

Zadatak 16.

Kutak za znatiželjne

Zanimljivost

Kolekcija zadataka 5

Zadatak 17.

Zadatak 18.

Zadatak 19.

Zadatak 20.

Zadatak 21.

Zanimljivost

Projekt

...i na kraju