

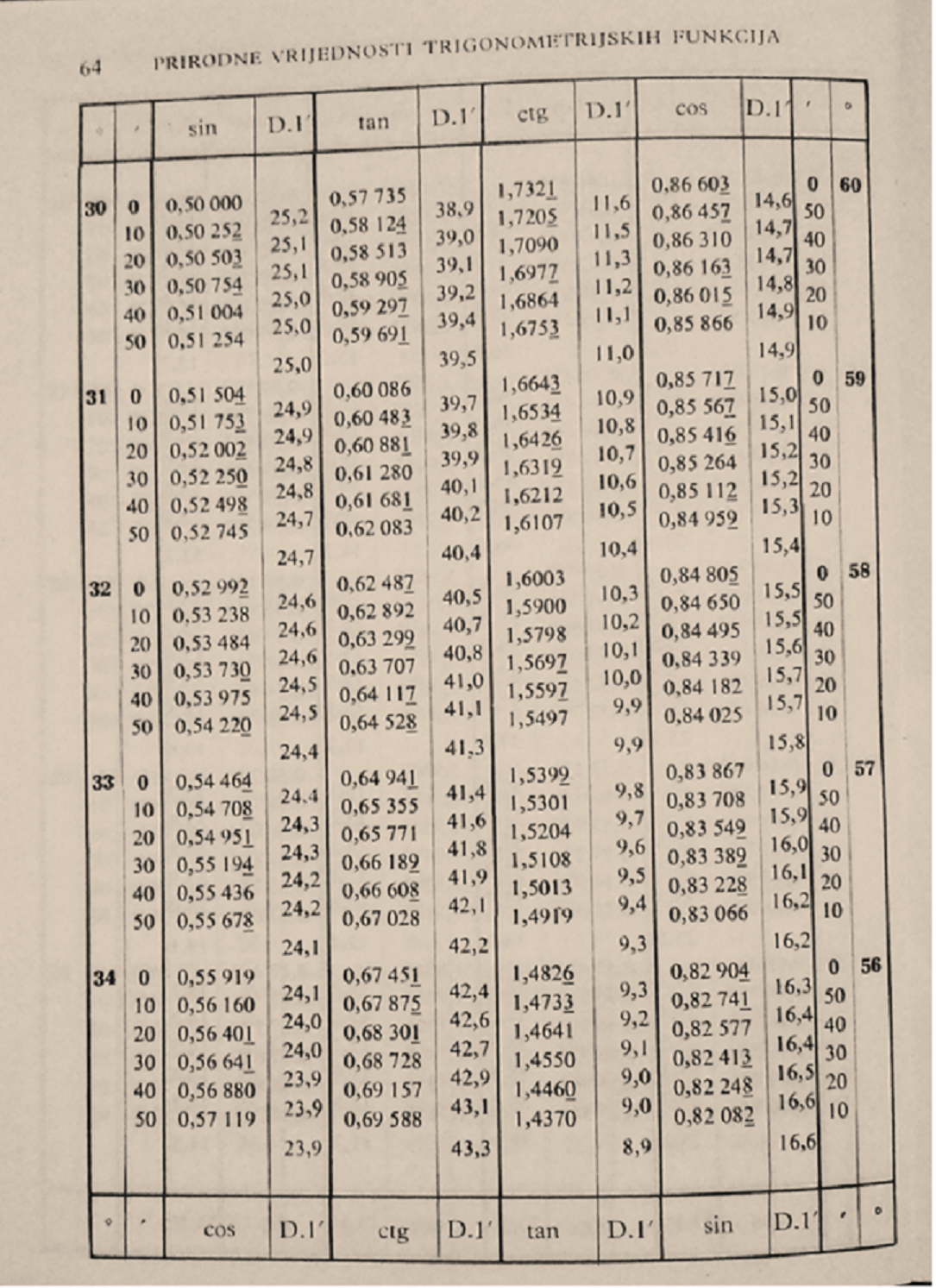
Na slici je dio tablica vrijednosti trigonometrijskih omjera. Tablice su se koristile za računanje s trigonometrijskim omjerima. Stupnjevi su zapisani u prvom i posljednjem stupcu. U istom su retku zapisani i i i tako dalje. Stupci s vrijednostima trigonometrijskih omjera označeni su dvostruko, sinus je u prvom redu i kosinus u posljednjem, tangens je u prvom i kotangens u posljednjem. Zašto?
U ovoj ćemo jedinici proučiti svojstva i veze trigonometrijskih omjera. Neka od tih svojstava objasnit će kako je organizirana tablica na slici.
Ponovite definicije trigonometrijskih omjera.
|
|
|
|
|
|
|
|
|
|
|
|
Odredili smo trigonometrijske omjere kutova od
i
Uočavate li u tablici veze trigonometrijskih omjera kutova od i Kutovi od i jesu komplementarni. Istražimo u sljedećem primjeru kako su povezani trigonometrijski omjeri komplementarnih kutova.
Primjer 1.
S pomoću klizača mijenjajte duljine kateta te promatrajte kutove trokuta i vrijednosti sinusa i kosinusa za prikazane kutove.
Primjer 2.
U sljedećoj aktivnosti također mijenjajte duljine kateta, ali ovaj put pratite što se događa s vrijednostima tangensa i kotangensa prikazanih kutova.
Povežite trigonometrijske omjere komplementarnih kutova
i
pravokutnog trokuta.
|
|
|
|
|
|
|
|
|
|
|
Zapišimo formule za trigonometrijske omjere komplementarnih kutova. Za komplementrarne kutove
i
vrijedi
pa umjesto
možemo pisati
Trigonometrijski omjeri komplementarnih kutova:
Primjer 3.
Pogledajmo ponovno tablicu s vrijednostima trigonometrijskih omjera. U istom su retku zapisani komplementarni kutovi. Sinus jednog od njih jednak je kosinusu drugog. Taj je broj zapisan u tablicama samo jedanput. Na primjer:
Pročitajte u tablici vrijednosti trigonometijskih omjera za kut od i za kut od Provjerite džepnim računalom.
Ponovno pogledajte gornje aktivnosti te odgovorite na postavljena pitanja.
Mogu li duljine stranica trokuta biti negativne?
Koja je najdulja stranica u pravokutnom trokutu?
Može li omjer nasuprotne katete i hiptenuze biti 0?
Mogu li vrijednosti sinusa i kosinusa šiljastih kutova biti negativne?
Mogu li vrijednosti sinusa i kosinusa biti veće od
Mogu li vrijednosti tangensa i kotangensa šiljastih kutova biti manje od
Mogu li vrijednosti tangensa i kotangensa šiljastih kutova biti veće od
Zaključimo.
S obzirom na to da smo sinus i kosinus šiljastih kutova definirali kao omjere kateta i hipotenuze, a hipotenuza je uvijek najdulja stranica u pravokutnom trokutu, taj je razlomak manji od ( bismo dobili kad bi kateta mogla biti jednako dugačka kao hipotenuza). Duljine stranica trokuta nikada ne mogu biti negativne, ni pa je zato taj razlomak uvijek pozitivan.
Kod tangensa i kotangensa kutova omjeri kateta mogu biti i veći od
ali ponovno ne negativni ni nula.
U pravokutnom trokutu vrijednosti sinusa i kosinusa šiljastih kutova uvijek su iz intervala a vrijednosti tangensa i kotangensa iz intervala tj.
Za koje realne brojeve postoje šiljasti kut takav da je
Uputa: Riješite sustav nejednadžbi i
Primjer 4.
U sljedećoj aktivnosti mijenjajte duljine kateta i pratite vrijednosti sinusa i kosinusa kutova te vrijednost izraza Kakve vrijednosti poprima izraz
Napomena
Pripazite na zapis kvadrata u trigonometrijskim omjerima.
Dokažimo osnovni trigonometrijski identitet.
Krenimo od lijeve strane jednakosti, uvrstimo
i
i primijenimo Pitagorin poučak:
Primjer 5.
U sljedećoj aktivnosti mijenjajte duljine kateta i pratite vrijednosti sinusa, kosinusa, tangensa i kotangensa, zatim omjere sinusa i kosinusa te kosinusa i sinusa. Uočavate li vezu između nekih podataka?
Zaključimo.
,
Dokažite prethodne tvrdnje.
Primjer 6.
Koristeći se osnovnim trigonometrijskim identitetima, dokažite:
Krenimo od lijeve strane jednakosti, kvadrirajmo izraz u zagradi i primijenimo da je
što smo i trebali dokazati.
Dokažite identitet:
Uputa: Uvrstite
i
pa svedite na zajednički nazivnik.
Primjer 7.
Za određivanje vrijednosti kotangensa nema tipke na džepnom računalu. Zato ćemo se snalaziti i upotrijebiti vezu između tangensa i kotangensa
PREFIKSNO: broj tipka tipka ( )
POSTFIKSNO: tipka broj (tipka ), tipka ( )
Postupak računanja kotengensa prikazan je u animaciji koja slijedi.
Primjer 8.
Za određivanje kuta kojemu je poznat kotangens opet se snalazimo i prelazimo na tangens upotrebom tipke ( ) i nakon toga određujemo
Na primjer, za daje i kut
Postupak određivanja kuta kojemu je poznata vrijednosti kotangensa možete pogledati u sljedećoj aktivnosti.
Napomena
Kotangens se sve rjeđe upotrebljava. Nema potrebe za njegovom upotrebom jer sve probleme za koje bismo eventualno mogli upotrijebiti kotangens možemo riješiti koristeći se tangensom.
Primjer 9.
Neka je Možemo li odrediti vrijednosti ostalih trigonometrijskih omjera kuta Dva su načina na koja to možemo učiniti: određivanjem kuta ili primjenom trigonometrijskih identiteta.
- Prvi način
Iz zadane vrijednosti sinusa, džepnim računalom odredimo kut Zatim, ponovno džepnim računalom, iz poznatog kuta odredimo ostale trigonometrijske omjere:
Drugi način
Iz osnovnog trigonometrijskog identiteta dobivamo:
Tangens računamo kao omjer sinusa i kosinusa:
Odredite ostale trigonometrijske omjere (na oba načina) ako je
Osnovnim trigonometrijskim identitetima povezali smo trigonometrijske omjere. Pri tome je veza sinusa i kosinusa sadržavala kvadrate, odnosno korijene. U primjeni su često prikladnije veze koje ne sadrže kvadriranje i korjenovanje. Potražimo takve veze.
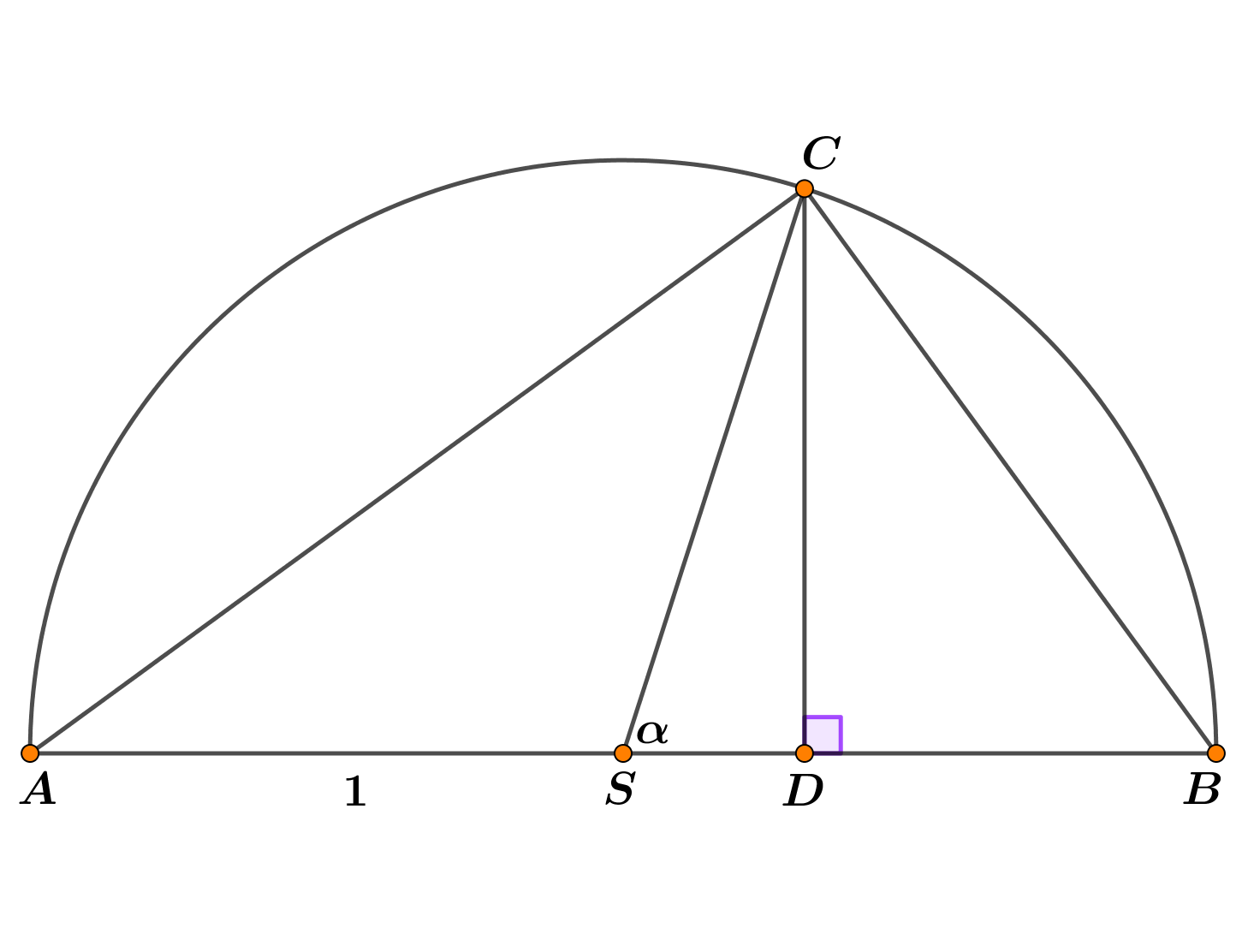
Na slici je polukružnica sa središtem u
polumjera 1. Što znamo o trokutu
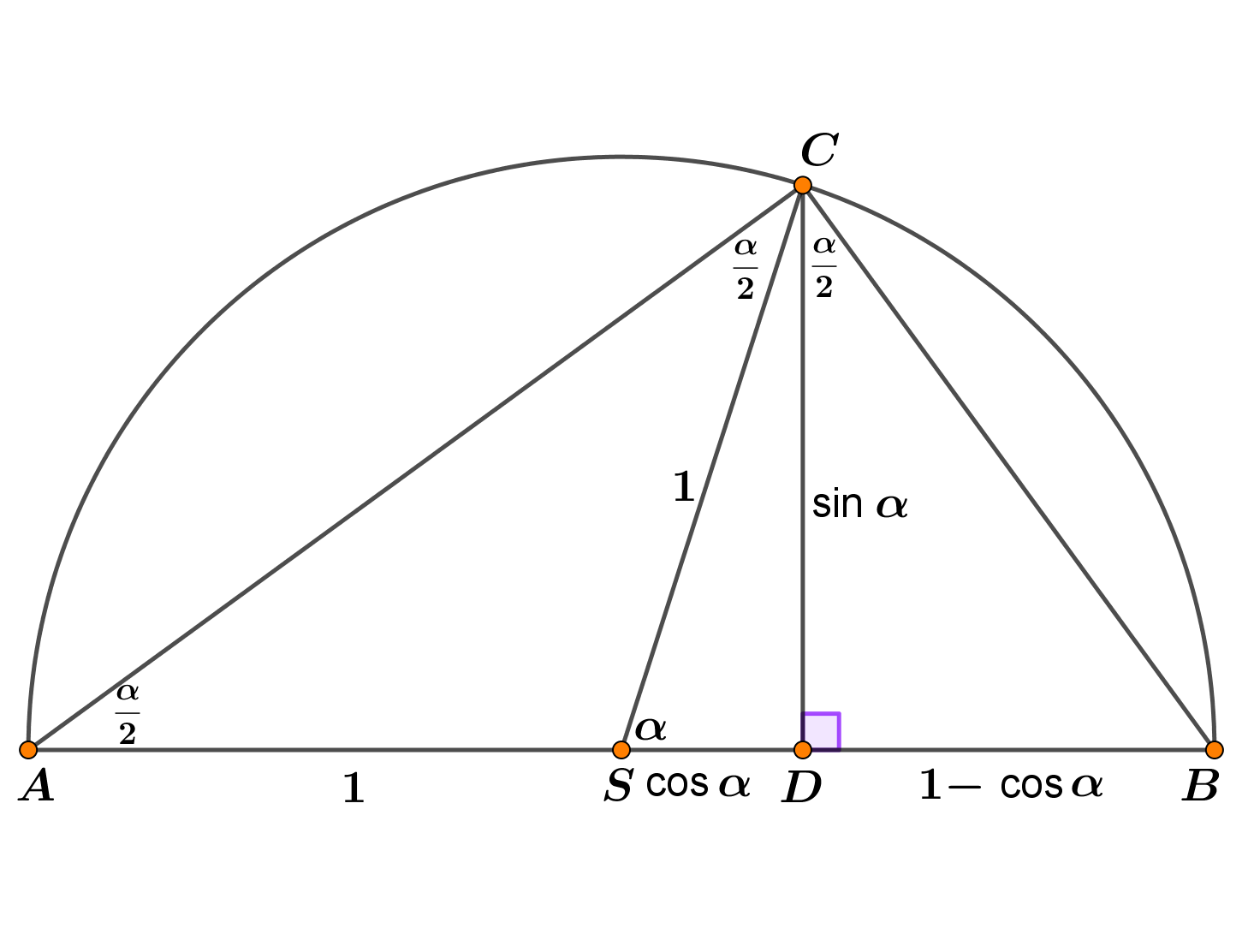
Trokut je pravokutan.
Označite pa koristeći identitete i dokažite:
pa je
iz čega slijedi tražena jednakost.
Određivali smo ostale trigonometrijske omjere ako je bio zadan sinus ili kosinus. Što ako je zadan tangens? Možemo li odrediti ostale trigonometrijske omjere bez računanja kuta?
Postavite oznake na odgovarajuća mjesta na stranicama pravokutnog trokuta.
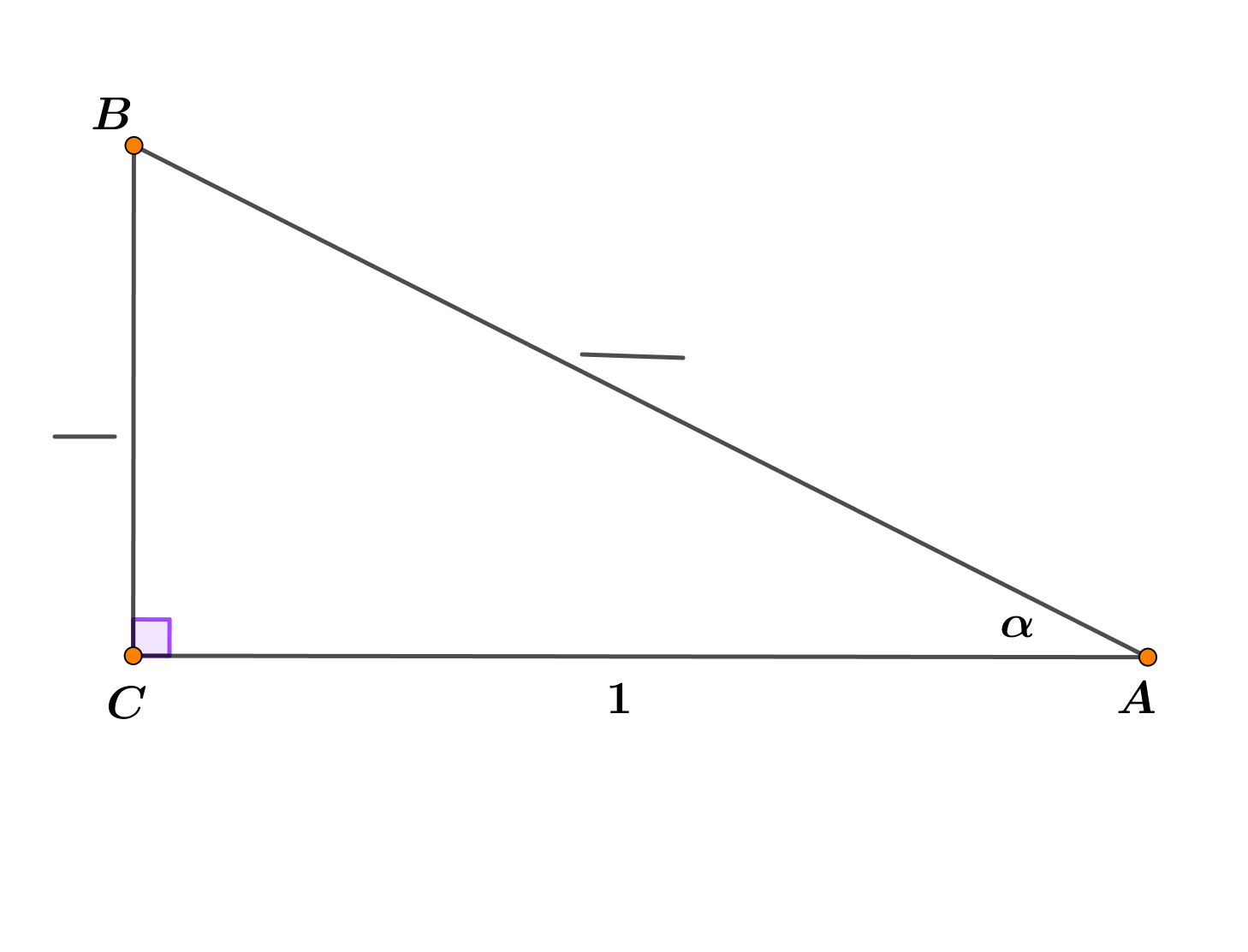
Koristeći se oznakama sa slike i definicijama trigonometrijskih omjera izrazite i pomoću