Matematika 4 - 2.3 Geometrijski niz

Na početku...

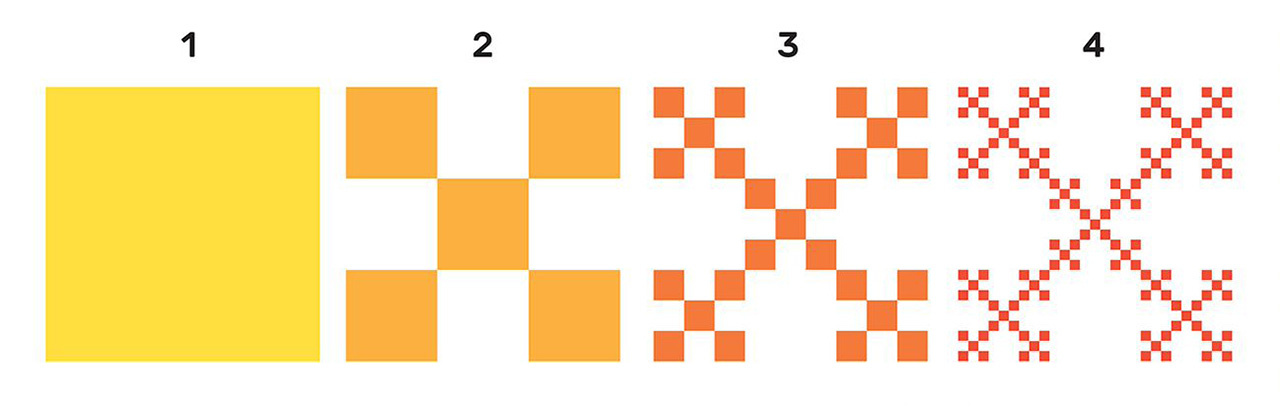
Prikazan je niz od 4 slike: 1 kvadrat, 5 kvadrata, 25 kvadrata, 125 kvadrata — Kvadrati u nizu

Koliko je kvadrata na svakoj slici u nizu? Zapišite dobivene brojeve u obliku niza i opišite kako se mijenjaju zapisani brojevi kvadrata.

Istražimo

Ako nastavimo crtati kvadrate na prikazani način, na sljedećoj će slici biti

kvadrata.

Na slici s rednim brojem

8

bit će

kvadrata.

Uočimo da je broj kvadrata potencija broja

null

Ako znamo broj kvadrata na slici s rednim brojem $n - 1,$ odnosno ako je poznat član niza $a_{n - 1},$ tada je član $a_{n}$ jednak

a_{n} = a_{n - 1} + 5

a_{n} = 5 a_{n - 1}

a_{n} = 10 a_{n - 1}

a_{n} = 25 a_{n - 1} .

null

Formula za opći član niza brojeva kvadrata je

a_{n} = 5 n

a_{n} = n^{5}

a_{n} = 5^{n - 1}

a_{n} = 5^{n} .

null

Primjer 1.

Promotrimo sljedeće nizove.

a. $2,$ $6,$ $18,$ $54,$ $. . .$

b. $- 6,$ $- 3,$ $- 1.5,$ $- 0.75,$ $. . .$

c. $1.2,$ $- 12,$ $120,$ $- 1 200,$ $. . .$

Popunite sljedeću tablicu u bilježnici.

Niz $a_{1}$ $a_{5}$ $a_{10}$ $a_{11}$ $a_{n - 1}$ $a_{n}$ $\frac{a_{n}}{a_{n - 1}}$

a.

b.

c.

Niz	$a_{1}$	$a_{5}$	$a_{10}$	$a_{11}$	$a_{n - 1}$	$a_{n}$	$\frac{a_{n}}{a_{n - 1}}$
a.	$2$	$162$	$2 \cdot 3^{9}$	$2 \cdot 3^{10}$	$2 \cdot 3^{n - 2}$	$2 \cdot 3^{n - 1}$	$3$
b.	$-6$	$-0.375$	$- 6 \cdot {0.5}^{9}$	$- 6 \cdot {0.5}^{10}$	$- 6 \cdot {0.5}^{n - 2}$	$- 6 \cdot {0.5}^{n - 1}$	$0.5$
c.	$1.2$	$12 000$	$1.2 \cdot {(- 10)}^{9}$	$1.2 \cdot {(- 10)}^{10}$	$1.2 \cdot {(- 10)}^{n - 2}$	$1.2 \cdot {(- 10)}^{n - 1}$	$- 10$

Postoji li neka zajednička karakteristika nizova pod a., b., c. i niza kvadrata iz uvodnog primjera?

Zadatak 1.

Počevši od drugog člana niza, svaki se član niza dobije

prethodnog

člana uvijek istim brojem različitim od nule. Stoga je, počevši od drugog člana niza,

svakog člana i člana neposredno ispred njega konstantan.

null

Zadatak 2.

Dopunite članovima koji nedostaju tako da omjer svakog člana i člana neposredno ispred njega uvijek bude isti broj.

3,

21,

1 029,

. . .

null

- 1,

- 16,

64,

1 024,

. . .

null

- 5,

- \frac{64}{5},

- \frac{512}{25},

. . .

Pomoć:

Vrijedi $\frac{a_{3}}{a_{2}} = \frac{a_{2}}{a_{1}} .$

null

Geometrijski niz; količnik geometrijskog niza;kvocijent geometrijskog niza

Za niz $(a_{n})$ u kojem je svaki član, počevši od drugog, jednak umnošku prethodnog člana i konstante $q \neq 0$ kažemo da je geometrijski niz. Pišemo

$a_{n} = a_{n - 1} \cdot q,$ $n \in N,$ $n > 1 .$

Kvocijent svakog člana geometrijskog niza i člana neposredno ispred je konstantan i jednak $q .$ Pišemo

$q = \frac{a_{2}}{a_{1}} = \frac{a_{3}}{a_{2}} = . . . = \frac{a_{n}}{a_{n - 1}},$ $n > 1 .$

Za konstantu $q$ kažemo da je količnik ili kvocijent geometrijskog niza.

Zadatak 3.

Provjerite jesu li sljedeći nizovi geometrijski.

a. $2,$ $4,$ $6,$ $8,.. .$

Pomoć:

Svaki se sljedeći član dobije dodavanjem broja $2 .$

null

b. $\frac{4}{3},$ $\frac{2}{3},$ $\frac{1}{3},$ $\frac{1}{6}, .. .$

Pomoć:

Kvocijent susjednih članova je $\frac{1}{2} .$

null

c. $\sqrt{3},$ $\sqrt[3]{3},$ $\sqrt[6]{3}, 1,.. .$

Pomoć:

Kvocijent niza je $\frac{1}{\sqrt[6]{3}} .$

null

Zadatak 4.

Zapišite prvih pet članova geometrijskog niza ako je zadan prvi član i kvocijent.

a_{1} = 3,

q = 2

null

a_{1} = - 2,

q = - 0.5

null

a_{1} = - 0.25,

q = 4

null

Zašto geometrijski?

Primjer 2.

Promotrimo uzastopne članove geometrijskog niza $2,$ $6,$ $18,$ $54,$ $162,.. .$

Budući da je kvocijent uzastopnih članova konstantan, vrijedi

$\frac{18}{6} = \frac{6}{2} \Rightarrow 6^{2} = 2 \cdot 18,$ $\frac{54}{18} = \frac{18}{6} \Rightarrow 18^{2} = 6 \cdot 54,$ $\frac{162}{54} = \frac{54}{18} \Rightarrow 54^{2} = 18 \cdot 162 . . . .$

Ako to zapišemo s pomoću korijena, $6 = \sqrt{2 \cdot 18},$ $18 = \sqrt{6 \cdot 54},$ $54 = \sqrt{18 \cdot 162} . . .,$ uočit ćemo da je broj $6$ geometrijska sredina brojeva $2$ i $18,$ da je broj $18$ geometrijska sredina brojeva $6$ i $54.. .$

Općenito, za uzastopne članove geometrijskog niza vrijedi $\frac{a_{n + 1}}{a_{n}} = \frac{a_{n}}{a_{n - 1}} \Leftrightarrow {a_{n}}^{2} = a_{n - 1} \cdot a_{n + 1} .$

Ako imamo niz s pozitivnim članovima, ovo možemo pisati u obliku $a_{n} = \sqrt{a_{n - 1} \cdot a_{n + 1}} .$

Kažemo da je svaki član geometrijskog niza, osim prvog, jednak geometrijskoj sredini susjednih članova.

Kutak za znatiželjne

Pokažite da je svaki član geometrijskog niza s pozitivnim članovima jednak geometrijskoj sredini članova koji su jednako udaljeni od njega:

$a_{n} = \sqrt{a_{n - k} \cdot a_{n + k}},$ $1 \leq k \leq n - 1,$ $n > 1 .$

Zadatak 5.

Brojevi

\frac{1}{2} x,

x + 1,

2 (x + 3)

bit će tri uzastopna člana geometrijskog niza ako je

x =

Tada su članovi danog niza brojevi

Postupak:

Rješenje se dobije rješavanjem jednadžbe ${(x + 1)}^{2} = \frac{1}{2} x \cdot 2 (x + 3) .$

Zbroj prvih n članova geometrijskog niza

Koliko je ukupno kvadrata u nizu na slici iz uvodnog primjera?

Broj kvadrata čini geometrijski niz kojemu je prvi član jednak $1,$ a kvocijent $5 .$ Dakle, imamo niz $1,$ $5,$ $5^{2},$ $5^{3},$ $5^{4}, .. .$

Zbroj prvih četiriju članova lako ćemo izračunati: $1 + 5 + 5^{2} + 5^{3} = 156 .$

Koliko je ukupno kvadrata ako se niz sastoji od $100$ članova, $1 000$ članova, $n$ članova?

Za veliki broj članova nema smisla zbrajati jedan po jedan član, već treba pokušati pronaći formulu za računanje zbroja prvih $n$ članova geometrijskog niza.

Sljedeći video pomoći će nam da dođemo do formule.

Zadatak 9.

Zašto je bitan uvjet $q \neq 1 ?$ U kojem koraku izvoda se taj uvjet koristi?

Na kraju izvoda se dijeli s izrazom $q - 1$ pa taj izraz ne smije biti jednak $0 .$

Zbroj prvih n članova geometrijskog niza

Zbroj prvih $n$ članova geometrijskog niza kojemu je prvi član $a_{1}$ i kvocijent $q$ jednak je

$S_{n} = a_{1} + a_{1} q + a_{1} q^{2} + . . . + a_{1} q^{n - 1} = a_{1} \frac{q^{n} - 1}{q - 1},$ $q \neq 1 .$

Katkad se formula zapisuje u obliku $S_{n} = a_{1} \frac{1 - q^{n}}{1 - q} .$

Primjer 4.

Odredimo zbroj prvih deset članova geometrijskog niza $\frac{1}{2},$ $1,$ $2,$ $4,$ $8,.. .$

$S_{10} = \frac{1}{2} \cdot \frac{2^{10} - 1}{2 - 1} = 511.5 .$

Zadatak 10.

a. U geometrijskom je nizu

a_{1} = - 8,

q = - 2 .

Tada je zbroj prvih osam članova

S_{8} =

null

b. Zbroj geometrijskog niza od

6

članova kojemu je prvi član jednak

0.5,

a drugi

- 3

iznosi

null

Zadatak 11.

Odredite zbroj prvih $10$ članova geometrijskog niza kojemu nisu svi članovi pozitivni i za koji vrijedi da je $a_{1} = 1,$ $a_{3} - a_{2} = 6 .$

$a_{1} q^{2} - a_{1} q = 6$

$q^{2} - q - 6 = 0$

$q_{1} = 3, q_{2} = - 2$ – jer niz nije s pozitivnim članovima

$S_{10} = \frac{{(- 2)}^{10} - 1}{- 2 - 1} = \frac{1023}{- 3} = - 341$

Zadatak 12.

U geometrijskom nizu koji ima $20$ članova četvrti član jednak je $40,$ a sedmi član $320 .$ Koje su od sljedećih jednakosti točne?

a_{1} = 2

q = 2

S_{20} = 1 048 575

S_{20} = 5 242 875

a_{20} = 2 621 440

null

Zadatak 13.

a. Zbroj brojeva

\frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + \frac{1}{2^{5}} + . . . + \frac{1}{2^{15}}

iznosi

Traženi broj zapiši u decimalnom zapisu i zaokruži na jedno decimalno mjesto.

null

b. Zbroj brojeva

4^{4} + 4^{5} + 4^{6} + 4^{7} + 4^{8} + 4^{9} + 4^{10}

iznosi

null

Zadatak 14.

U igri memory geometrijske nizove određene s prvim članom i kvocijentom uparujete ili s prva $4$ člana pojedinog niza ili s pripadajućim općim članom.

Povećaj interaktivni prikaz

...i na kraju

Na slici je razgranato stablo s puno lišća. — Rast drveta

Pomoću nekog geometrijskog niza opišite rast drveta kao na fotografiji. Možete opisati porast broja grana i/ili porast broja listova i napraviti vlastite skice.

$a_{1}$	$- \frac{32}{125}$
$a_{4}$	$- 4$
$a_{2}$	$- \frac{16}{25}$
$a_{3}$	$- \frac{8}{5}$

2.3 Geometrijski niz

Na početku...

Istražimo

Primjer 1.

Zadatak 1.

Zadatak 2.

Geometrijski niz; količnik geometrijskog niza;kvocijent geometrijskog niza

Zadatak 3.

Zadatak 4.

Zašto geometrijski?

Primjer 2.

Kutak za znatiželjne

Zadatak 5.

Opći član geometrijskog niza

Zadatak 6.

Opći član geometrijskog niza

Zadatak 7.

Primjer 3.

Zadatak 8.

Zbroj prvih n članova geometrijskog niza

Zadatak 9.

Zbroj prvih n članova geometrijskog niza

Primjer 4.

Zadatak 10.

Zadatak 11.

Zadatak 12.

Zadatak 13.

Zadatak 14.

...i na kraju