


Rimljani su se latinskom riječi limes koristili za granicu između dvaju posjeda, odnosno utvrđeni obrambeni sustav koji se prostirao graničnim područjima radi obrane Rimskog Carstva. Pritom je limes mogao biti umjetno podignuta granica u obliku bedema, nasipa, kule za promatranje, rovova i sl. Rimski su limesi bili: Antoninov zid i Hadrijanov zid u Britaniji, Limes Germanicus u Germaniji, Dunavski limes, Trajanov zid u istočnoj Europi, Limes Alutanus i Limes Transalutanus u Daciji, Limes Arabicus u Arabiji i Limes Tripolitanus u Libiji.
"Jedini način da se otkriju granice mogućeg jest ići iznad njih u nemoguće."
Arthur C. Clarke
Kao što vidimo, pojam limesa ili granice postoji od davnina i inspiracija je mnogima.
Otkrijmo što je limes niza.
Primjer 1.
Smjestite prvih sedam članova niza zadanog općim članom na brojevni pravac. Ako nastavimo smještati članove niza na brojevni pravac, kojemu će se broju približavati?
Što je broj
veći, to se članovi niza sve više približavaju nuli. Pokušat ćemo preciznije matematički opisati što to znači.
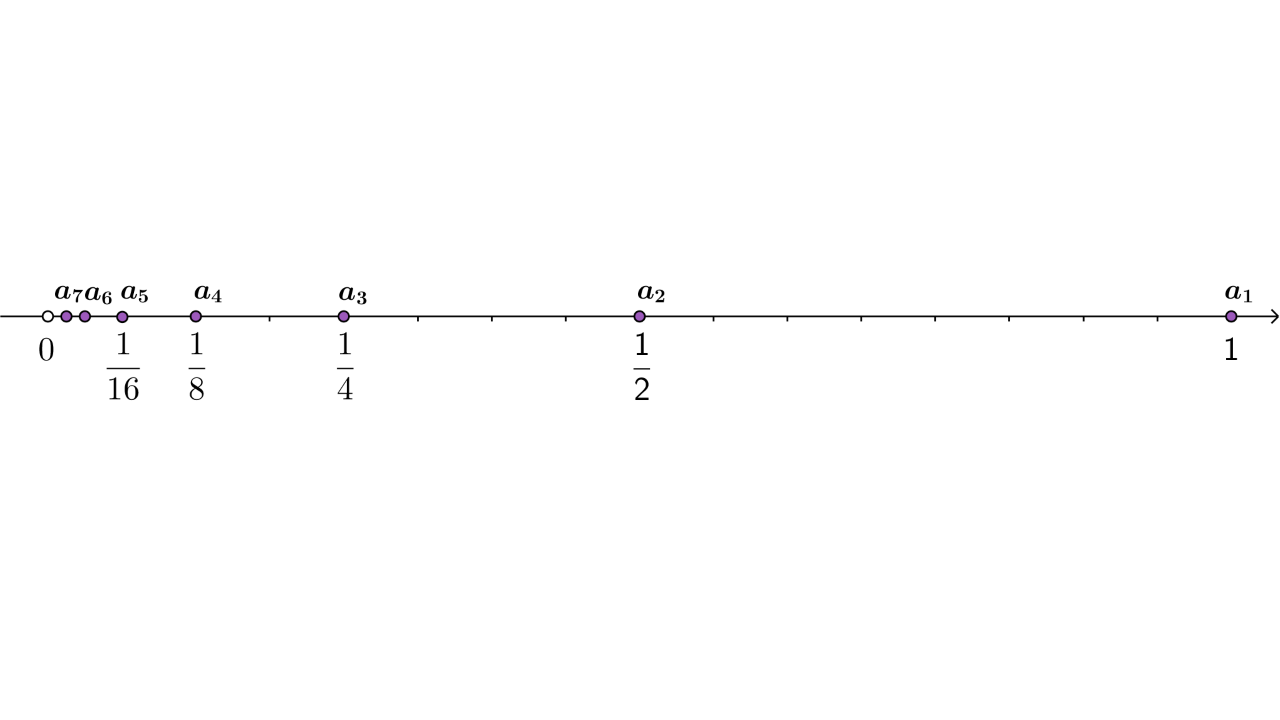
Promatrat ćemo što se događa oko nule, odnosno na nekom malom simetričnom intervalu oko nule, kao što je interval
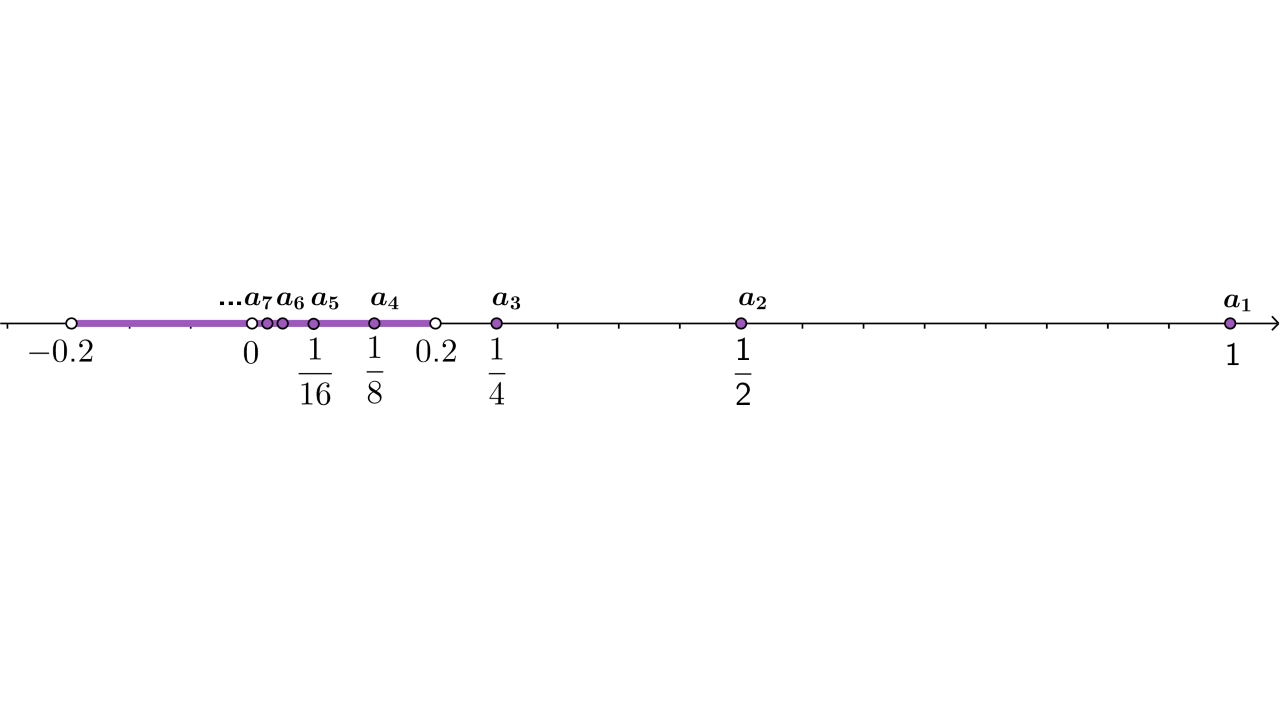
Pokušajmo još malo smanjiti interval oko nule, primjerice na interval
Pogledajmo sliku.
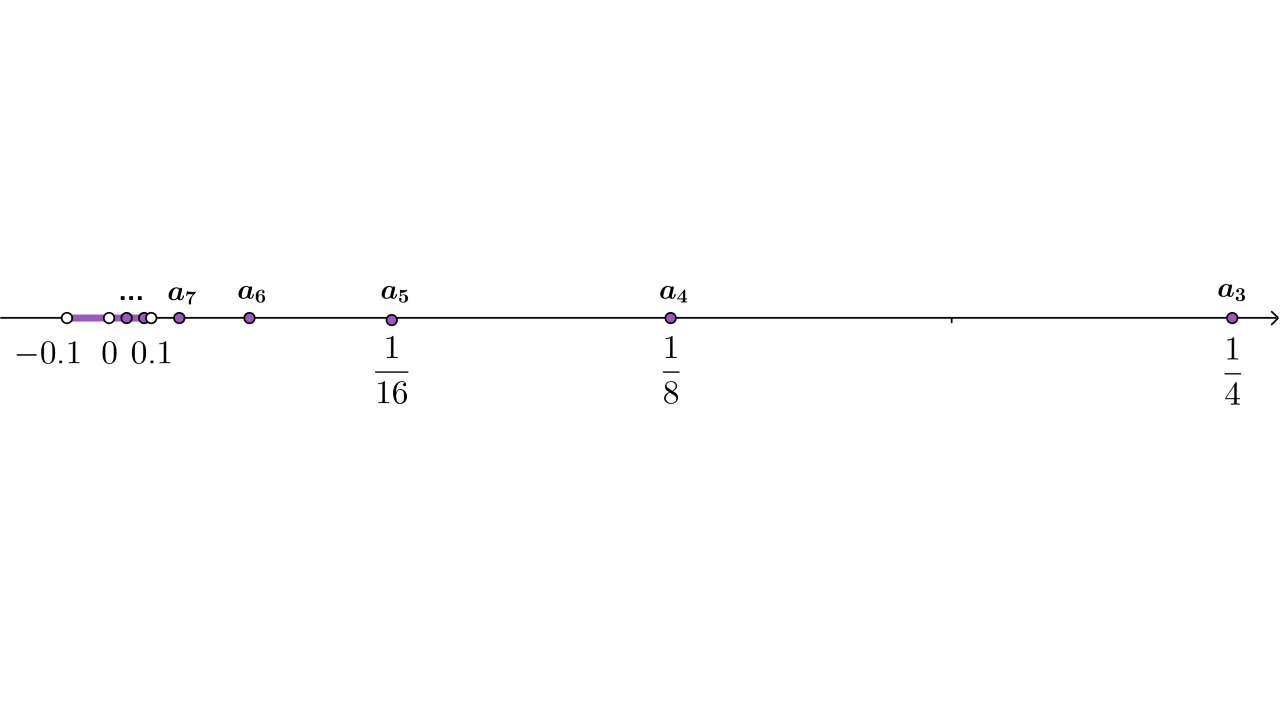
Odredimo broj članova niza koji su izvan i broj članova niza koji su unutar intervala
Za više od od nule udaljeno je
Pomoć:
Izvan zadanog intervala ih je
što je konačno mnogo.
Nije teško zaključiti da će, koliko god da se približimo nuli, konačan broj članova niza
ostati izvan tog malog intervala oko nule, a unutar njega bit će svi ostali članovi tog niza.
U tom slučaju kažemo da je nula granična vrijednost ili limes niza
Primjer 2.
Pogledajmo još jedan primjer niza i njegovu graničnu vrijednost.
Neka je niz zadan s općim članom Promotrimo u sljedećoj interakciji grafički prikaz tog niza.
Kako se mijenja vrijednost članova niza ovisno o broju Kojemu će se broju približavati članovi tog niza?
Provjerite, kao i u prošlom primjeru, hoće li unutar svakog, po volji malog, intervala oko broja biti gotovo svi članovi niza?
Mijenjajte udaljenost od broja odnosno interval a zatim odredite broj ( ) članova niza koji su izvan tog intervala.
a. Granična vrijednost ili broj kojemu se približavaju članovi niza
s povećanjem broja
je broj
b. Koliko je članova tog niza izvan intervala
c. Koji su članovi tog niza unutar intervala
d. Koliko je članova tog niza izvan intervala
e. Koji su članovi tog niza unutar intervala
f. Koliko je članova tog niza unutar intervala
g. Koliko je članova tog niza izvan intervala
Uočimo da se izvan svakog malog intervala oko broja
nalazi samo konačan broj članova niza,
a svi su ostali članovi niza, njih beskonačno mnogo, unutar tog intervala. Za broj
to ne vrijedi, izvan intervala
nalazi se beskonačno članova niza. Prema tome, graničnu vrijednost nekog niza definiramo na sljedeći način.
Za realni broj kažemo da je limes ili granična vrijednost niza ( ) realnih brojeva ako se izvan svakog, po volji malog, intervala oko broja nalazi samo konačno mnogo članova tog niza.
Zapisujemo
i čitamo "limes niza
kad
teži u beskonačnost je
".
Kažemo još da niz (
) teži ili konvergira prema
kad
teži u beskonačnost.
Za niz brojeva koji ima limes kažemo da je konvergentan.
Ako niz brojeva nema limes, kažemo da je divergentan.
U sljedećoj su interakciji grafički prikazani neki nizovi. Jesu li konvergentni ili divergentni? Obrazložite svoj zaključak.
Među prikazanim nizovima nalazi se konstantan niz
Očito je da izvan svakog, po volji malog, intervala oko broja
nema članova tog niza, odnosno da su svi članovi niza unutar tog intervala, pa vrijedi
Konstantan niz s općim članom je konvergentan i vrijedi
Primjer 3.
Promotrimo aritmetički niz Svaki njegov član, osim prvog, veći je od prethodnog za tri, pa je niz rastući i njegovi članovi teže u beskonačnost. Stoga je to divergentan niz.
Koliko je njegovih članova manje od Koliko ih je veće od Koliko je članova manje, a koliko veće od
Koliko je članova manje, a koliko veće od nekog velikog broja
Tri su člana zadanog niza manja od
a svi su ostali veći od
Usporedimo opći član niza s
Dakle, manja od
su
člana, a većih od
je beskonačno mnogo.
Usporedimo opći član niza s
Takvih je prirodnih brojeva
samo konačno mnogo, pa je konačno mnogo članova niza manjih, a beskonačno mnogo onih većih od
Za niz kažemo da teži u beskonačnost ako za svaki, po volji veliki, odabrani realni broj, postoji samo konačno mnogo članova niza koji su od njega manji. Da niz teži u beskonačnost, pišemo
Analogno se definira i niz koji teži u minus beskonačno. Pokušajte sami zapisati što bi značilo da je
Možda će vam pomoći sljedeći zadatak.
Niz je
Istražimo
Navedite primjere nekoliko različitih aritmetičkih nizova i opišite njihovu konvergenciju. Što zaključujete?
Aritmetički niz s općim članom i razlikom divergentan je i vrijedi Ako je razlika onda je
a. Koji od sljedećih nizova teže u beskonačnost?
b. Koji od sljedećih nizova teže prema nuli?
c. Koji od sljedećih nizova teže u minus beskonačno?
Uočimo da vrijedi
Zaključujemo:
Ako je tada je
Je li istinita sljedeća tvrdnja?
Ako je
tada je
Ako vrijedi, obrazložite zbog čega vrijedi.
Ako ne vrijedi, pronađite primjer i pokušajte popraviti tvrdnju tako da vrijedi.
Dana tvrdnja općenito ne vrijedi. Vrijedi za niz s pozitivnim članovima.
Primjer niza za koji ne vrijedi je niz
kojemu su članovi
Tada niz
s članovima
teži prema nuli. Niz
nije konvergentan, neparni članovi po redu teže u
a parni u
Ispravna tvrdnja glasi: Ako je
tada je
Razvrstajte sljedeće nizove, zadane s općim članom, ovisno o tome konvergiraju li u
ili ostalo.
Istražimo
U prvom smo primjeru imali geometrijski niz s općim članom i pokazali da je njegov limes jednak nuli. Zanima nas što je s konvergencijom bilo kojeg geometrijskog niza.
Istražite konvergenciju geometrijskog niza u sljedećim primjerima i odgovorite na pitanja koja slijede.
Niz a:
Niz b:
Niz c:
Niz d:
Niz e:
Postoji li geometrijski niz koji teži broju Ili broju
Ne postoji, osim ako se ne radi o konstantnom nizu kojemu je kvocijent jednak
Uočimo da vrijede sljedeće tvrdnje.
Geometrijski niz s kvocijentom konvergentan je i teži u nulu ako je Za geometrijski je niz divergentan.
Pritom za niz teži u beskonačnost, za limes ne postoji, a za niz je konstantan.
Uparite limes niza i njegov iznos.
|
|
|
|
|
|
|
|
ne postoji |
|
|
Do sada smo uglavnom naslućivali limes nizova ispisivanjem njihovih članova ili na temelju grafičkog prikaza. Nakon što naslutimo limes nekog niza, poželjno je dokazati da je taj broj limes koristeći se definicijom.
Dokažite da je
Prema definiciji treba pokazati da se izvan svakog, po volji malog, intervala oko nule nalazi samo konačno mnogo članova tog niza, a svi ostali članovi su unutar tog intervala.
Uobičajeno se neki mali interval oko
označava s
pri čemu je
Pogledajmo koliko je članova niza izvan tog intervala. Budući da su članovi niza pozitivni brojevi, dovoljno je vidjeti za koliko članova tog niza vrijedi da je
odnosno
Tada je
za sve
Prirodnih brojeva za koje ova nejednakost vrijedi ima samo konačno mnogo, pa je tvrdnja dokazana.
Na primjer, ako je
To znači da je samo konačno mnogo članova niza koji su izvan intervala
a svi ostali ili njih beskonačno, unutar je tog intervala.
Nije za sve nizove jednostavno naslutiti i dokazati da je neki broj njihov limes. Stoga se pri računanju limesa niza koriste neki od limesa jednostavnih nizova koje smo do sada opisali i sljedeća pravila za računanje limesa.
Neka su i konvergentni nizovi, a konstanta. Tada vrijedi:
- (limes zbroja ili razlike)
- (limes umnoška niza s konstantom)
- (limes umnoška)
- pri čemu su svi i (limes kvocijenta)
Ova pravila nećemo dokazivati, ali ćemo pokazati na primjerima kako se koriste pri računanju limesa niza. Pogledajmo sljedeći video.
a. Poredajte korake u redoslijedu računanja limesa
b.
Poredajte korake u redoslijedu računanja limesa
Ponekad je jednostavnije dokazati da je neki niz konvergentan, nego izračunati njegov limes. Pritom se obično koristi omeđenost niza.
Omeđen niz
Kažemo da je niz omeđen ako postoje realni brojevi i tako da za sve članove niza vrijedi
Primjer 4.
Jesu li sljedeći nizovi omeđeni?
a.
Uočite da je opći član niza uvijek manji od
i da je niz rastući.
Vrijedi za sve članove niza, pa je niz omeđen.
b. Niz je rastući geometrijski niz, nije omeđen.
c. Niz je omeđen jer su mu jedine vrijednosti članova i
Koji su od tih nizova konvergentni? Jesu li omeđeni nizovi uvijek konvergentni?
Niz
konvergira,
Niz
je geometrijski s kvocijentom većim od jedan, pa teži u beskonačnost.
Niz
nije konvergentan, a omeđen je.
Dakle, omeđeni niz ne mora biti konvergentan. Ali, ako je omeđeni niz rastući ili padajući, onda će biti i konvergentan.
Omeđeni niz koji je monoton (rastući ili padajući) jest konvergentan.
Označite točne tvrdnje. Niz
je
Kroz sljedeću igru provjerite koliko ste dobro svladali limes niza.