

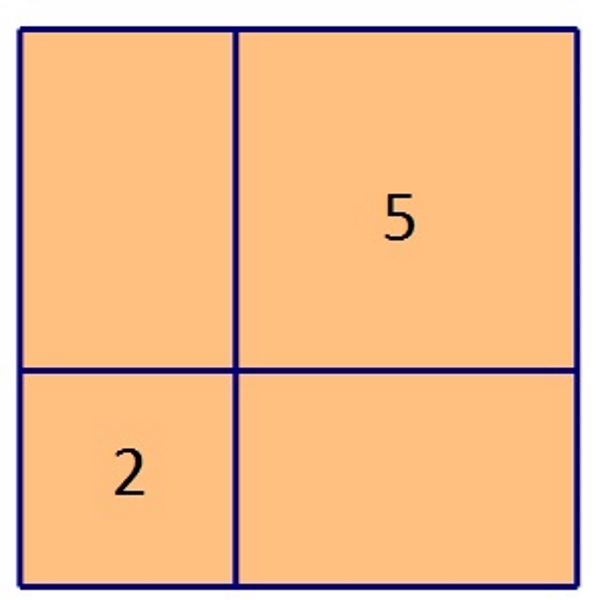
Dijelovi kvadrata su dva manja kvadrata površine dva i pet kvadratnih metara.
Izračunajmo opseg i površinu kvadrata na slici.
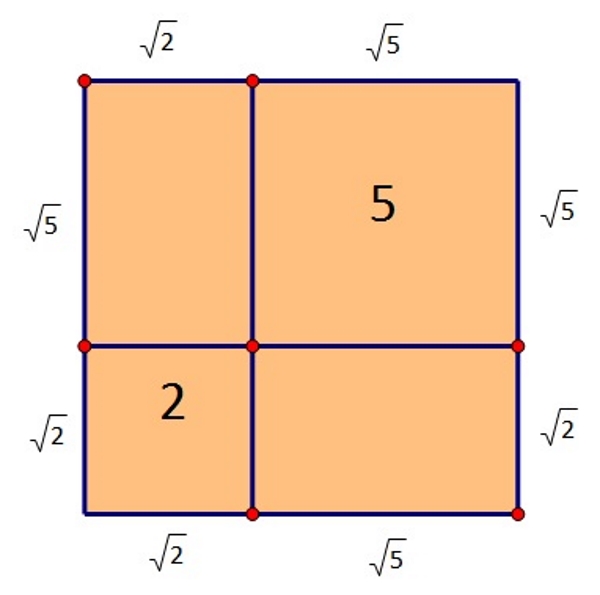
Iz iznosa površina odredimo duljine stranica kako je prikazano na slici.
Kvadrat površine ima duljinu stranice
Kvadrat površine ima duljinu stranice
Opseg kvadrata iznosi:
Površina kvadrata iznosi:
.
Prepoznajmo kvadrat zbroja i prisjetimo se formule,
Površina kvadrata iznosi kvadratna metra.
Primjer 1.
Pojednostavnimo i izračunajmo kvadrat zbroja.
Izračunajte i pojednostavnite do kraja izraze te spojite s odgovarajućim izrazom.
Spojite parove.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
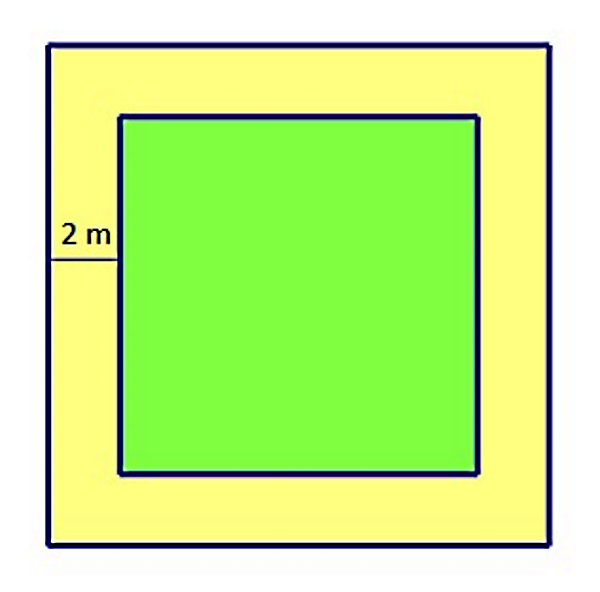
Površina travnatog igrališta u obliku kvadrata iznosi kvadratnih metara.
Igralište će biti smanjeno zbog izrade biciklističke staze širine metra.
Kolika je nova površina travnatog igrališta?
Kako je širina staze metra, duljina stranice smanjena je za metra. Duljinu stranice smanjenog igrališta označimo s metara.
Pojednostavnjeni izraz za smanjenu duljinu stranice iznosi metara.
Izraz za površinu smanjenog igrališta iznosi
Prepoznajmo kvadrat razlike i podsjetimo se formule
Nova, smanjena površina igrališta iznosi
Površina smanjenog igrališta iznosi
četvornih metara.
Složite pločice tako da prislonite stranice s jednakim vrijednostima. Pritiskom na tipku POMOĆ srednja će pločica biti postavljena u točan položaj.
Primjer 2.
Izračunajmo vrijednost zadane razlike kvadrata koristeći se formulom
Prema formuli za razliku kvadrata i slijedi:
Pojednostavnite i izračunajte zadanu razliku kvadrata.
Postupak:
Postupak:
Postupak:
Postupak:
Postupak:
Postupak:
U sljedećem nizu zadataka smjestite povlačenjem brojeve i/ili znakove tako da jednakost bude točna. Smjestite točno na sredinu za to predviđenog prostora.
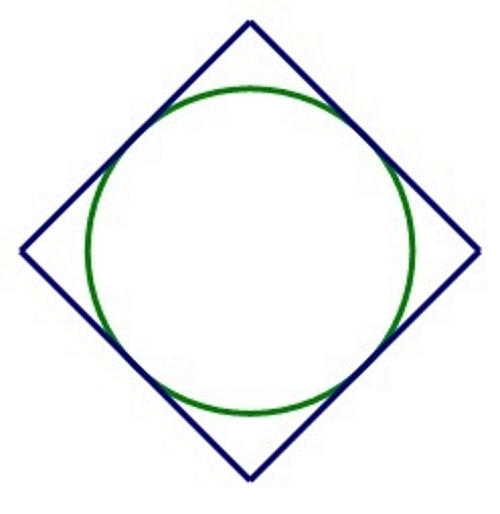
Izračunajte površinu i opseg kruga upisanog u kvadrat površine
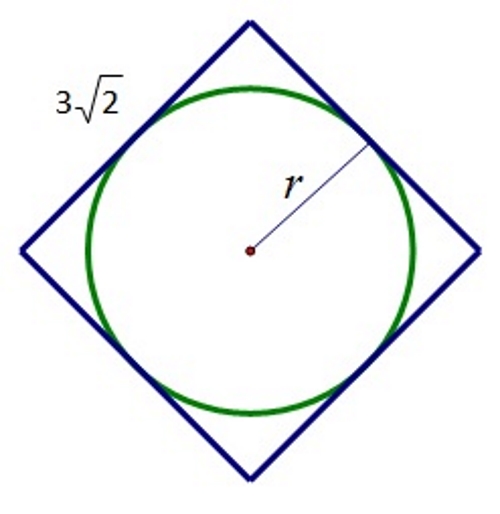
Za izračun površine i opsega kruga potrebna nam je duljina polumjera kruga
Duljina promjera kruga jednaka je duljini stranice kvadrata,
Duljina polumjera jednaka je polovini duljine stranice kvadrata,
Izračunajmo duljinu stranice kvadrata iz njegove površine,
Duljina stranice kvadrata iznosi
Duljina polumjera iznosi
Opseg tog kruga iznosi približno
Površina tog kruga iznosi približno

Na slici je prikaz kvadratne zelene površine od
Unutar nje je betonska kružna staza širine
Vanjski je krug upisan kvadratu.
Kolika je površina travnatog dijela?
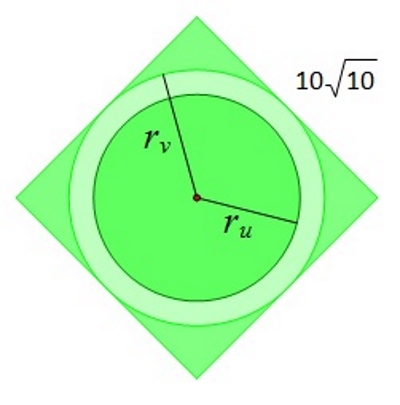
Od površine kvadrata treba oduzeti površinu vanjskog kruga te mu dodati površinu unutarnjeg kruga. U animaciji je prikazana ideja rješavanja zadatka.
Površina travnatog dijela iznosi približno
kvadratnih metara.
Izračun rješenja:
Duljina polumjera vanjskog kruga
Račun:
Duljina polumjera unutarnjeg, manjeg kruga
Izraz za površinu travnjaka:
Površina travnatog dijela iznosi približno
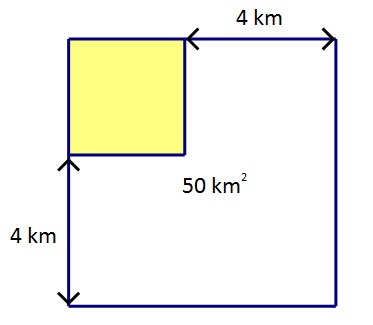
Na parceli u obliku kvadrata površine
Kolika će biti površina ograđenog dijela?
Kolika je duljina ograde kojom je dio ograđen?
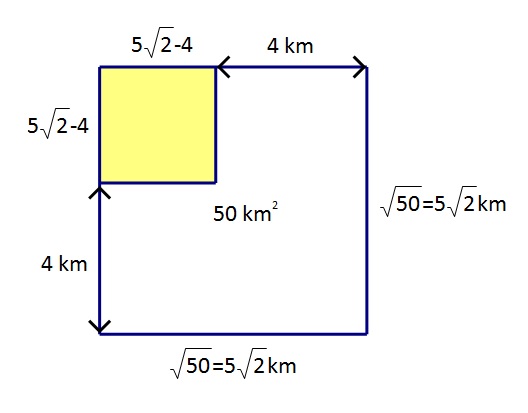
Duljinu stranice velikog kvadrata
Duljina stranice malog kvadrata iznosi
Površina ograđenog dijela jednaka je površini kvadrata sa stranicom duljine
Površina ograđenog dijela iznosi
Duljina ograde kojom je ograđen dio jednaka je opsegu kvadrata sa stranicom duljine
Duljina ograde iznosi
O množenju binoma koji sadržavaju izraze s korijenima.
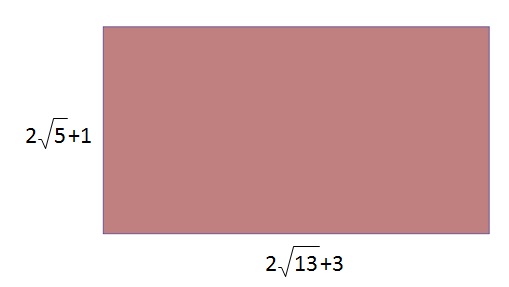
Izračunajte površinu pravokutnika na slici.
Površina pravokutnika jednaka je umnošku duljina susjednih stranica,
Prvo se izračunavaju izrazi u zagradama (ako zagrade postoje), nakon toga se kvadrira ili korjenuje, zatim množi i dijeli, a tek na kraju zbraja i oduzima.
Spojite izraz s korijenima s njegovim pojednostavnjenim oblikom.
Spojite parove.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
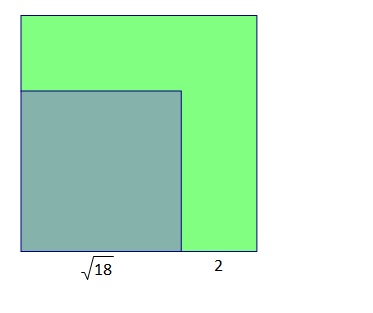
Odredite razliku površina većeg i manjeg kvadrata na slici.
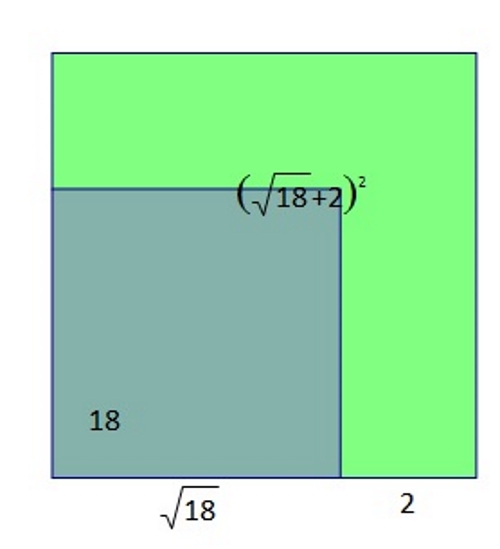
Razliku površina većeg i manjeg kvadrata označimo s
Površina većeg kvadrata je
Duljina stranice manjeg kvadrata iznosi
Površina manjeg kvadrata je
Izraz za razliku površina jednak je razlici kvadrata. Prisjetimo se formule za razliku kvadrata
Razlika površina kvadrata iznosi

Vrata su u obliku pravokutnika.
Širina je vrata
Visina i širina vrata su u omjeru
Kolika je visina tih vrata?
Označimo visinu vrata s
Iz uvjeta zadatka slijedi:
Visina vrata približno iznosi

Izračunajte površinu pravokutnika na slici.
Površina pravokutnika jednaka je umnošku duljina susjednih stranica.
Neka su duljine stranica
Površina pravokutnika iznosi
Pojednostavnite izraz.
Pojednostavnite izraz.
Pojednostavnite izraz.
U nizu zadataka samo je jedan odgovor točan.
Postupak:
Postupak:
Postupak:
Postupak:
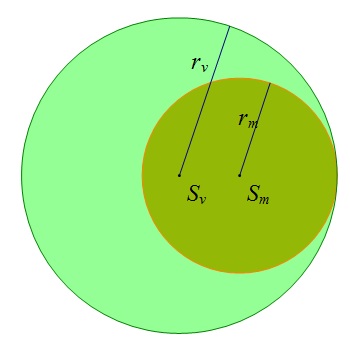
Na slici su dvije kružnice koje se dodiruju iznutra.
Omjer je njihovih polumjera
Koliki je omjer površina krugova određenih tim kružnicama?
Omjer duljina polumjera iznosi
gdje su
Oznaka
Za površine vrijedi
Omjer je površina tih krugova
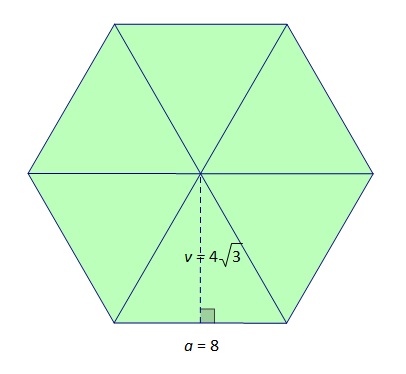
Površina pravilnog šesterokuta na slici jednaka je zbroju površina šest sukladnih jednakostraničnih trokuta
Površina pravilnog šesterokuta na slici iznosi
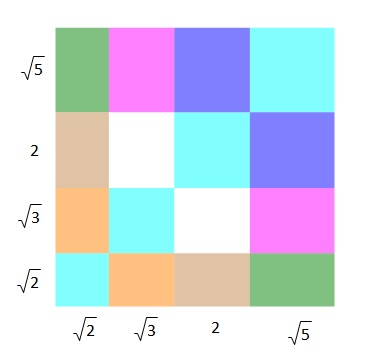
Naučili smo:
Koristeći se džepnim računalom, utvrdite točnost tvrdnje.
Koristeći se džepnim računalom, utvrdite točnost tvrdnje.
Koristeći se džepnim računalom, utvrdite točnost tvrdnje.
Spojite parove.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Razvrstajte brojeve u skupine.
Izračunajte površinu i opseg pravokutnika s duljinama stranica: