Matematika 8 - Aktivnosti za samostalno učenje

Približno računanje drugog korijena

Heronov postupak

Heron je približno izračunavao drugi korijen koristeći se formulom $\sqrt{a^{2} + h} \approx a + \frac{h}{2 a},$ gdje je broj $h$ malen u usporedbi s brojem $a .$ Primjerice,

$\sqrt{51} = \sqrt{49 + 2} \approx 7 + \frac{2}{2 \cdot 7} = 7 + \frac{1}{7} = \frac{50}{7} .$

Izračunamo li s pomoću džepnog računala vrijednost broja $\sqrt{51}$ na tri decimale, dobit ćemo $7.141,$ dok je decimalna vrijednost razlomka $\frac{50}{7},$ zaokružena na tri decimale, jednaka $7.143 .$

Dakle, pogreška je jako malena!

U sljedećem videoisječku pogledajmo primjenu Heronova postupka na još nekoliko primjera.

Heronov postupak približnog računanja drugog korijena

Kolekcija zadataka 1

Zadatak 1.

Na slici je Heron iz Aleksandrije, starogrčki matematičar. — Heron iz Aleksandrije

Koristeći se opisanim Heronovim postupkom, odredite približnu vrijednost drugog korijena sljedećih brojeva.

$68$
$105$
$34$

$\sqrt{68} = \sqrt{64 + 4} \approx 8 + \frac{4}{2 \cdot 8} = 8 + \frac{1}{4} = \frac{33}{4}$
$\sqrt{105} = \sqrt{100 + 5} \approx 10 + \frac{5}{2 \cdot 10} = 10 + \frac{1}{4} = \frac{41}{4}$
$\sqrt{34} = \sqrt{36 + (- 2)} \approx 6 + \frac{- 2}{2 \cdot 6} = 6 + \frac{- 1}{6} = \frac{35}{6}$

Zadatak 2.

Koristeći se džepnim računalom, provjerite za koliko se razlikuju približne od stvarnih vrijednosti. (Rezultate zaokružite na tri decimale).

$\sqrt{68} \approx 8.246$ dok je $\frac{33}{4} = 8.250$

$\sqrt{105} \approx 10.247$ dok je $\frac{41}{4} = 10.250$

$\sqrt{34} \approx 5.831$ dok je $\frac{35}{6} \approx 5.833$

Zatvori

Zanimljivost

Zanima li vas povijest matematike, pročitajte članak Petra Mladinića o Računanju (drugog i trećeg) korijena na način koji potječe vjerojatno iz starog Babilona. Članak je objavljen u časopisu Matka broj 98 (prosinac 2016.).

Kolekcija zadataka 2

Zadatak 3.

Koji su od brojeva racionalni, a koji nisu?

\sqrt{3} \cdot \sqrt{5} \cdot \sqrt{10}

\frac{5^{2}}{\sqrt{3}}

\frac{\sqrt{2}}{\sqrt{8}}

{(2 + \sqrt{3})}^{2}

\sqrt{\frac{2}{15}} \cdot \sqrt{\frac{6}{5}}

\sqrt{1 \frac{32}{49}}

\sqrt{\frac{3}{4}} : \sqrt{\frac{3}{25}}

(2 - \sqrt{7}) (2 + \sqrt{7})

\sqrt{4 \frac{1}{9}}

Racionalni brojevi

Nisu racionalni

null

Zadatak 4.

Poredajte brojeve prema veličini, počevši od najmanjeg.

$\frac{\sqrt{3}}{\sqrt{2}} . \sqrt{\frac{12}{8}}$
$\sqrt{1.69}$
$\frac{\sqrt{6}}{2}$
$\frac{3}{\sqrt{5}}$
$\sqrt{1 \frac{40}{81}}$

Pomoć:

Brojeve napišite u decimalnom zapisu s točnošću na tri decimale.

null

Zadatak 5.

Svakom zadatku pridružite rješenje.

$\sqrt{6} : \sqrt{18}$	$4 \sqrt{3}$
$1.5 \sqrt{3} + 2.5 \sqrt{3}$	$\sqrt{3}$
$\frac{3}{4} \sqrt{3} + \frac{1}{2} \sqrt{3} - \frac{1}{8} \sqrt{3}$	$\frac{\sqrt{3}}{3}$
$\sqrt{12} - \frac{5}{6} \sqrt{12} - \frac{1}{3} \sqrt{12}$	$\frac{9}{8} \sqrt{3}$

Pomoć:

Pojednostavnite zadane izraze.

null

Zadatak 6.

Provjerite ispravnost jednakosti.

$\sqrt{2 \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$
$\sqrt{3 \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$
$\sqrt{4 \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$

Uočavate li pravilnost u jednakostima? Kakvog su oblika zadani mješoviti brojevi?

$\sqrt{2 \frac{2}{3}} = \sqrt{\frac{8}{3}} = \frac{\sqrt{8}}{\sqrt{3}} = \frac{2 \sqrt{2}}{\sqrt{3}} = 2 \frac{\sqrt{2}}{\sqrt{3}} = 2 \sqrt{\frac{2}{3}}$
$\sqrt{3 \frac{3}{8}} = \sqrt{\frac{27}{8}} = \frac{\sqrt{27}}{\sqrt{8}} = \frac{3 \sqrt{3}}{\sqrt{8}} = 3 \frac{\sqrt{3}}{8} = 3 \sqrt{\frac{3}{8}}$
$\sqrt{4 \frac{4}{15}} = \sqrt{\frac{64}{15}} = \frac{\sqrt{64}}{\sqrt{15}} = \frac{4 \sqrt{4}}{\sqrt{15}} = 4 \frac{\sqrt{4}}{\sqrt{15}} = 4 \sqrt{\frac{4}{15}}$

Zatvori

Zanimljivost

Ako je mješoviti broj moguće napisati u obliku zbroja $a + \frac{a}{a^{2} - 1},$ onda vrijedi:

$\sqrt{a + \frac{a}{a^{2} - 1}} = a \sqrt{\frac{a}{a^{2} - 1}} .$

$\sqrt{a + \frac{a}{a^{2} - 1}} = \sqrt{\frac{a (a^{2} - 1) + a}{a^{2} - 1}} = \sqrt{\frac{a^{3} - a + a}{a^{2} - 1}} = \sqrt{\frac{a^{3}}{a^{2} - 1}} = \frac{\sqrt{a^{3}}}{\sqrt{a^{2} - 1}} = \frac{a \sqrt{a}}{\sqrt{a^{2} - 1}} = a \frac{\sqrt{a}}{\sqrt{a^{2} - 1}} = a \sqrt{\frac{a}{a^{2} - 1}}$

Kolekcija zadataka 3

Zadatak 7.

Koji je od sljedećih računa korektan?

\sqrt{6} + \sqrt{3} = \sqrt{6 + 3} = \sqrt{9} = 3

Pazi!
Zbroj korijena nije jednak korijenu zbroja.

\sqrt{15} - \sqrt{6} = \sqrt{15 - 6} = \sqrt{9} = 3

Pazi!
Razlika korijena nije jednaka korijenu razlike.

\sqrt{4 \frac{4}{9}} = \sqrt{4} \sqrt{\frac{4}{9}} = 2 \frac{2}{3}

Mješoviti broj prvo napiši u obliku razlomka.

\sqrt{5 \frac{5}{24}} = \sqrt{\frac{125}{24}} = \frac{\sqrt{125}}{\sqrt{24}} = \frac{5 \sqrt{5}}{\sqrt{24}} = 5 \sqrt{\frac{5}{24}}

\sqrt{5 \frac{5}{24}} = \sqrt{\frac{125}{24}} = \frac{\sqrt{125}}{\sqrt{24}} = \frac{5 \sqrt{5}}{\sqrt{24}} = 5 \sqrt{\frac{5}{24}}

null

Zadatak 8.

Djelomično korjenujte zadane brojeve. U prvi kvadratić postavite odgovarajući broj za koeficijent, a u drugi kvadratić pripadni radikand. Ako je zadani broj potpuni kvadrat, onda u drugi kvadratić postavite "prazan" kvadratić.

Zadatak 9.

Na slici je bazen kružnog oblika sa stazom oko njega. Staza je oblika kružnog vijenca.

Gradonačelnica Matkograda odlučila je proširiti sportski park Mokri svijet. Odlučila je sagraditi veliki bazen kružnog oblika promjera $20$ metara, a oko bazena izgraditi stazu. U skladištu su imali samo $140 m^{2}$ pločica koje su se svidjele gradonačelnici.

Kolika je najveća širina staze koju je moguće popločiti tim pločicama? Rezultat izrazite cijelim brojem u metrima.

Površina bazena jednaka je $p = r^{2} \cdot π = 10^{2} π \approx 314 m^{2},$ a površina staze oko bazena može biti najviše $140 m^{2} .$ To znači da vanjski krug ima ukupnu površinu od $314 + 140 = 454 m^{2} .$

Ako je poznata površina kruga, duljina njegova polumjera jednaka je $r = \sqrt{\frac{p}{π}} \approx \sqrt{\frac{454}{3.14}} \approx \sqrt{144.5860} \approx 12.02 m .$

Najveća je širina staze koja se može prekriti tim pločicama $2$ metra.

Zatvori

Povezani sadržaji

Indeks tjelesne mase

Indeks tjelesne mase ili BMI samo je okvirni pokazatelj za procjenu tjelesne mase.

Računa se na taj način da se tjelesna masa osobe ( $m$ ) u kilogramima podijeli s kvadratom visine ( $h$ ) u metrima: $BMI = \frac{m}{h^{2}} .$

Zanimljivost

Za jednu našu poznatu manekenku kažu da je visoka $180 cm,$ a masa joj je jedva $52 kg .$ Izračunamo li njezin BMI, dobit ćemo približno $16 .$ Prema podatcima iz tablice ‒ mlada je dama pothranjena!

BMI se ipak ne može uzeti kao relevantno mjerilo za procjenu debljine i zdravlja pojedine osobe jer ne uzima u obzir tjelesnu građu pojedinca. BMI ne može pokazati postotak masnog tkiva u odnosu prema mišićnoj ili koštanoj masi, a to su osnovni kriteriji za procjenu je li određena osoba debela ili mršava.
Pojedinci s velikom tjelesnom masom i visokim BMI indeksom ne mogu se automatski kategorizirati kao pretili. U sportaša ili krupno građenih ljudi, npr., udjel je mišićne i koštane mase u odnosu prema visini velik, ali to ne znači da su debeli.

Tablica indeksa tjelesne mase (BMI)
Interpretacija vrijednosti
Muškarci		Žene
$< 20.7$	BMI prenizak	$< 19.1$	BMI prenizak
$20.7 - 26.4$	BMI idealan	$19.1 - 25.8$	BMI idealan
$26.5 - 27.8$	BMI malo iznad normale	$25.9 - 27.3$	BMI malo iznad normale
$27.9 - 31.1$	BMI visok	$27.4 - 32.2$	BMI visok
$31.2 - 45.4$	BMI previsok	$32.3 - 44.8$	BMI previsok
$> 45.4$	BMI izrazito visok	$> 44.8$	BMI izrazito visok

Indeks tjelesne mase (BMI) računa se prema formuli $BMI = \frac{m}{h^{2}} .$

Ta je formula ekvivalentna formuli $h^{2} = \frac{m}{B M I},$ odnosno $h = \sqrt{\frac{m}{BMI}} .$

Zadatak 10.

Izračunajte visinu osoba kojima su poznati masa i BMI. Rezultate izrazite prirodnim brojem u centimetrima.

$m = 58 kg,$ BMI $= 21.6,$ $h =$

null

null
$m = 62 kg$ , BMI $= 18.3$ , $h =$

null

null
$m = 64 kg,$ BMI $= 22,$ $h =$

null

null
$m = 71 kg,$ BMI $= 26.9,$ $h =$

null

null
$m = 85 kg$ , BMI $= 30.1$ , $h =$

null

null

Uvrstite li zadane podatke u izraz $h = \sqrt{\frac{m}{BMI}},$ dobit ćete:

$h = \sqrt{\frac{58}{21.6}} \approx \sqrt{2.6852} \approx 1.638 m≈ 164 cm$
$h = \sqrt{\frac{62}{18.3}} \approx \sqrt{3.388} \approx 1.841 m≈ 184 cm$
$h = \sqrt{\frac{64}{22}} \approx \sqrt{2.9091} \approx 1.706 m≈ 171 cm$
$h = \sqrt{\frac{71}{26.9}} \approx \sqrt{2.6394} \approx 1.625 m≈ 163 cm$
$h = \sqrt{\frac{85}{30.1}} \approx \sqrt{2.8239} \approx 1.680 m≈ 168 cm$

Kutak za znatiželjne

Drugi i treći korijen

Primjer 1.

Zadan je kvadrat površine $36 m^{2} .$ Kolika je duljina njegove stranice?

Slika prikazuje kvadrat površine 36 kvadratnih metara

$P = a^{2}$

$36 = a^{2} .$

Izračunajmo drugi korijen iz $36 .$

$\sqrt{36} = 6$

Duljina je stranice tog kvadrata $6 m .$

Primjer 2.

Obujam kocke iznosi $8 m^{3} .$ Kolika je duljina brida te kocke?

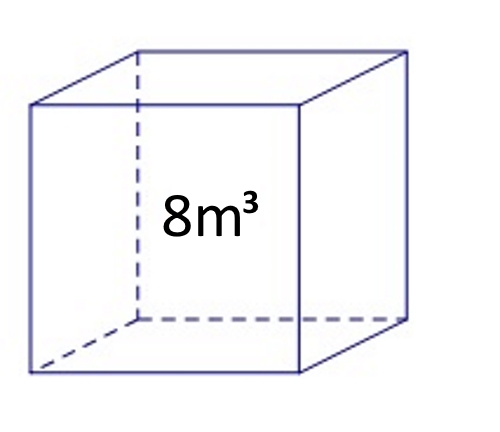
Slika prikazuje kocku čiji je obujam 8 kubičnih metara.

Obujam kocke računamo tako da pomnožimo duljinu, širinu i visinu kocke.

Ako je duljina brida $a$ , obujam je jednak

$V = a \cdot a \cdot a = a^{3},$

$8 = a^{3} .$

Pronađimo koji broj pomnožen sa samim sobom tri puta daje umnožak $8 .$

Odnosno, koji broj na treću potenciju daje broj $8 .$

To je broj $2 .$ Duljina je brida kocke $2 m .$

Zapravo smo izračunali treći korijen iz broja $8,$ što se zapisuje $\sqrt[3]{8} = 2 .$

Zadatak 11.

Spojite parove.

$\sqrt[3]{27}$	$6$
$\sqrt[3]{1 000}$	$4$
$\sqrt[3]{125}$	$3$
$\sqrt[3]{216}$	$10$
$\sqrt[3]{64}$	$5$

null

Tsunami

Tsunami je naziv za destruktivne valove koji najčešće nastaju kao posljedica poremećaja (potresa) na morskome dnu. Naziv tsunami japanskog je podrijetla, a znači val u luci.
Valovi tsunamija putuju brzinom koja se može približno opisati formulom $v \approx \sqrt{g h},$ gdje je $v$ brzina vala u metrima u sekundi, $g$ konstanta približne vrijednosti $9.81 {m/s}^{2},$ a $h$ dubina mora u metrima.

Kolekcija zadataka 4

Zadatak 12.

Ako je prosječna dubina oceana oko $3 500 m,$ izračunajte prosječnu brzinu tsunamija.

Prosječna brzina je približno $v \approx \sqrt{9.81 \cdot 3 500} \approx 185.30 m/s .$

Zadatak 13.

Koristeći se prosječnom brzinom tsunamija (iz prethodnog zadatka), izračunajte prosječnu udaljenost koju će tsunami prijeći u $2,$ $5,$ $6$ i $10$ sati. (Brzina je put prijeđen u jedinici vremena.)

Budući da $1$ sat ima $3 600$ sekundi, zaključujemo da u jednome satu tsunami prijeđe približno $667 080$ metara, tj. približno $667 km .$

Za $2$ sata tsunami će prijeći približno $1 334 km .$

Za $5$ sati tsunami će prijeći približno $3 335 km .$

Za $6$ sati tsunami će prijeći približno $4 002 km .$

Za $10$ sati tsunami će prijeći približno $6 670 km .$

Zadatak 14.

Izračunajte brzinu tsunamija na dubini od $1 200 m .$

Prosječna brzina je približno $v \approx \sqrt{9.81 \cdot 1 200} \approx 108.50 m / s .$

Zatvori

Kolekcija zadataka 5

Zadatak 15.

Izračunajte brzinu tsunamija na dubini od $2 500 m .$

Prosječna brzina je približno $v \approx \sqrt{9.81 \cdot 2 500} \approx 156.60 m / s .$

Zadatak 16.

Na kojoj je dubini brzina tsunamija približno $70 m/s ?$

Uvrštavanjem podataka u formulu $v \approx \sqrt{g \cdot h}$ dobivamo $70 \approx \sqrt{9.81 \cdot h} .$

Rješavanjem jednadžbe nalazimo da je $4 900 \approx 9.81 \cdot h,$ tj. da je $h \approx 499.49 m .$

Zadatak 17.

Je li brzina tsunamija na dubini od $1 000 m$ četiri puta veća od brzine tsunamija na dubini od $250 m ?$

Brzina tsunamija na $1 000$ metara dubine je približno $v \approx 99.05 m / s,$ a na dubini od $250$ metara približno $v \approx 49.52 m / s .$

Očito je da $99.05$ nije $4$ puta više od $49.52$

Zatvori

Jačina vjetra

Beaufortova ljestvica služi ocjenjivanju jačine vjetra prema njegovim učincima. Naziv je dobila po mornaričkom časniku i hidrografu koji ju je izradio 1806. godine.
Brzina vjetra prema Beaufortovoj ljestvici izražena je formulom $v = 0.837 \sqrt{B^{3}},$ gdje je $v$ brzina vjetra mjerena metrima u sekundi, a $B$ odgovarajući broj na Beaufortovoj ljestvici.

Jačina $(B f)$	Naziv	visina valova $(m)$
$0$	tišina	$0$
$1$	lahor	$0.1$
$2$	povjetarac	$0.2$ do $0.5$
$3$	slabi vjetar	$0.6$ do $1$
$4$	umjereni vjetar	$1$ do $2$
$5$	umjereno jaki vjetar	$2$ do $3$
$6$	jaki vjetar	$3$ do $4$
$7$	žestoki vjetar	$4$ do $5.5$
$8$	olujni vjetar	$5.5$ do $7$
$9$	jaki olujni vjetar	$7$ do $10$
$10$	orkanski vjetar	$10$ do $12$
$11$	jaki orkanski vjetar	$12$ do $15$
$12$	orkan	više od $15$

Zadatak 18.

Na fotografiji su valovi koje je izazvala bura na Jadranu.

Izračunajte brzinu vjetra (mjerenu metrima u sekundi) ako je njegova jačina prema Beaufortovoj ljestvici jednaka:

$1$
$3$
$8$
$9$
$12 .$

Rezultate za okružite na $3$ decimale.

$v = 0.837 m/s$
$v = 4.349 m/s$
$v = 18.939 m/s$
$v = 22.599 m/s$
$v = 34.793 m/s$

Zanimljivost

Najsnažniji zabilježeni udar vjetra u Hrvatskoj izmjeren je 23. prosinca 2003. godine, na autocesti A1, između tunela Sveti Rok i Maslenica, na vijaduktu Božići. Tada je jedan od rijetkih instrumenata za mjerenje brzine vjetra, koji je uopće uspio neoštećen izdržati nalete vjetra, zabilježio brzinu od $307 km/h,$ što je neslužbeno najveća dosad izmjerena brzina vjetra u Hrvatskoj. Zbog toga što taj instrument nije bio predviđen za tolike iznose, podatak se ne uzima kao službeni.

(izvor: http://www.crometeo.hr/koje-su-najvece-brzine-vjetra-izmjerene-u-hrvatskoj/)

Kolekcija zadataka 6

Zadatak 19.

Brzine vjetra iz rezultata prethodnog zadatka izrazite u kilometrima na sat. Rezultate zaokružite na $3$ decimale.

$v = 3.013 km/h$
$v = 15.656 km/h$
$v = 68.180 km/h$
$v = 81.356 km/h$
$v = 125.255 km/h$

Zadatak 20.

Brzina vjetra iznosi $6$ metara u sekundi. Kojem broju na Beaufortovoj ljestvici odgovara ta brzina?

Uvrštavanjem dobivamo da je $6 = 0.837 \cdot \sqrt{B^{3}},$ odakle je $B^{3} \approx 51.387 .$

Budući da je $3^{3} = 27,$ a $4^{3} = 64,$ zaključujemo da je $3 < B < 4 .$

Budući da je broj $B$ prirodan broj i da je $51.387$ bliže broju $64$ nego broju $27,$ zaključujemo da brzina vjetra od $6$ metara u sekundi odgovara broju $4$ na Beaufortovoj ljestvici.

Zadatak 21.

Brzina vjetra iznosi $45 km$ na sat. Kojem broju na Beaufortovoj ljestvici odgovara ta brzina?

Brzina od $45 km$ na sat odgovara brzini od $12.5$ metara u sekundi.

Analognim postupkom kao u prethodnom zadatku nalazimo da je $B^{3} \approx 223 .$

Budući da je $6^{3} = 216,$ zaključujemo da je $B \approx 6 .$

Zadatak 22.

Kao službeno najjači udar vjetra iz NNE smjera u Hrvatskoj i dalje vrijedi onaj od 21. prosinca 1998. godine s Masleničkog mosta kada je zabilježen udar bure od $248 km/h .$ Kojem broju na Beaufortovoj ljestvici odgovara ta brzina?

Brzina od $248 km$ na sat odgovara brzini od približno $68.9$ metara u sekundi.

Analognim postupkom kao u prethodnom zadatku nalazimo da je $B^{3} \approx 6 776 .$

Budući da je $19^{3} = 6 859,$ zaključujemo da je $B \approx 19 .$

Zatvori

Zanimljivost

Drugi službeno najjači udar vjetra, također bure, zabilježen je na Paškome mostu i iznosio je $65.2 m/s .$ Treći najjači udar bure izmjeren je na Krčkome mostu i iznosio je $221.8 km/h,$ što se dogodilo u vrijeme ciklone Teodor, 11. studenog 2013.

Četvrti najjači udar zabilježen je u Makarskoj i iznosio je $59 m/s,$ tj. $212.4 km/h .$ Također se radilo o buri.

Peti najjači udar vjetra u Hrvatskoj, juga, zabilježen je na Palagruži s $56.9 m/s,$ tj. $204.84 km/h .$

Udar bure u Splitu 14. studenog 2004. godine (ciklona Dorothy) iznosio je $174.6 km/h .$

Od većih gradova još vrijedi spomenuti Dubrovnik sa $159.48 km/h$ i Šibenik sa $146 km/h .$

(izvor: http://www.crometeo.hr/koje-su-najvece-brzine-vjetra-izmjerene-u-hrvatskoj/)

Kolekcija zadataka 7

Zadatak 23.

Jaka bura u akvatoriju otoka Silbe dizala je valove visine do $7$ metara. Kolikom je brzinom puhala (mjereno u kilometrima na sat)?

Valove visine $7$ metara diže vjetar čija jačina prema Beaufortovoj ljestvici iznosi $8 .$

Brzina tog vjetra je približno $18.94 m/s,$ ili približno $68 km/h .$

Zadatak 24.

Tramontana kod otoka Palagruže diže valove maksimalne visine do $8.5$ metara. Kolikom brzinom, izraženo u metrima u sekundi, puše?

Valove visine do $8.5$ metara diže vjetar čija jačina prema Beaufortovoj ljestvici iznosi $9 .$

Brzina tog vjetra je približno $22.6 m/s,$ ili približno $81.4 km/h .$

Zatvori

Na početku...

Približno računanje drugog korijena

Kolekcija zadataka 1

Zadatak 1.

Zadatak 2.

Zanimljivost

Kolekcija zadataka 2

Zadatak 3.

Racionalni brojevi

Nisu racionalni

Zadatak 4.

Zadatak 5.

Zadatak 6.

Zanimljivost

Kolekcija zadataka 3

Zadatak 7.

Zadatak 8.

Zadatak 9.

Povezani sadržaji

Zanimljivost

Zadatak 10.

Kutak za znatiželjne

Drugi i treći korijen

Zadatak 11.

Tsunami

Kolekcija zadataka 4

Zadatak 12.

Zadatak 13.

Zadatak 14.

Kolekcija zadataka 5

Zadatak 15.

Zadatak 16.

Zadatak 17.

Jačina vjetra

Zadatak 18.

Zanimljivost

Kolekcija zadataka 6

Zadatak 19.

Zadatak 20.

Zadatak 21.

Zadatak 22.

Zanimljivost

Kolekcija zadataka 7

Zadatak 23.

Zadatak 24.