


Petra je izgradila kvadrate nad stranicama pravokutnog trokuta. Prebrojila je da je za izgradnju najmanjeg kvadrata trebala 9 kockica, a za izgradnju najvećega 25 kockica. Koliko je kockica trebala za izgradnju kvadrata nad duljom katetom? Može li se zadatak riješiti bez prebrojavanja?
Za izgradnju kvadrata nad duljom katetom Petri je bilo potrebno 16 kockica, što se može odrediti prebrojavanjem. Kako bismo do rješenja došli brže, možemo prebrojiti samo broj kockica u jednome redu, 4, te kvadriranjem izračunati ukupan broj kockica 42=16.
No zadatak se može riješiti i bez ikakva prebrojavanja s pomoću primjene Pitagorina poučka.
Zbroj površina kvadrata nad katetama pravokutnog trokuta jednak je površini kvadrata nad njegovom hipotenuzom.
Zatim je
9+x=25, odnosno
x=16.
S pomoću animacije koja slijedi prisjetite se Pitagorina poučka.
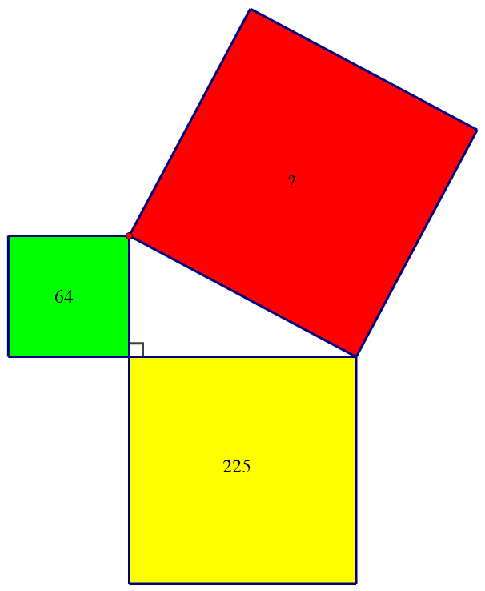
Kolika je površina kvadrata nad hipotenuzom? Kolike su duljine stranica pravokutnog trokuta sa slike?
Površina kvadrata nad hipotenuzom iznosi p=64+225=289.
Duljina kraće katete iznosi
√64=8, duljina dulje katete
√225=15, a duljina hipotenuze
√289=17.
Primjer 1.
Zadan je pravokutni trokut s pravim kutom u vrhu C. Izračunajte duljinu treće stranice tog trokuta ako je zadano:
- a=40cm, b=9cm
- b=9cm, c=15cm
- c=29cm, a=21cm.
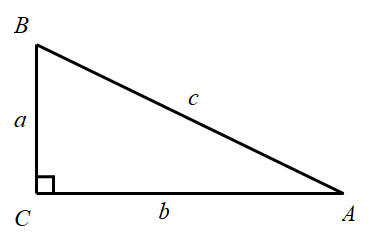
a=40cm
b=9cm
c=?
Površina kvadrata nad stranicom a iznosi 402=1600, a površina kvadrata nad stranicom b iznosi 92=81. Zato je površina kvadrata nad hipotenuzom 1600+81=1681 c=√1681=41cm.
Kraće, poznate podatke možemo uvrstiti u općenitu formulu Pitagorina poučka.
c2=a2+b2
c2=402+92
c2=1681
c=√1681=41cm
b=9cm
c=15cm
a=?
a2=c2-b2
a2=152-92
a2=144
a=√144=12cm
c=29cm
a=21cm
b=?
b2=c2-a2
b2=292-212
b2=400
b=√400=20cm
Zadan je pravokutni trokut
ABC s katetama duljine
a=12cm
i
b=35cm. Izračunajte duljinu hipotenuze tog trokuta.
a=12cm
b=35cm
c=?
c2=a2+b2
c2=122+352
c2=1369
c=√1369=37cm
Duljina hipotenuze tog trokuta iznosi 37cm.
Primjer 2.
Zadan je pravokutni trokut ABC s hipotenuzom duljine c=53cm i katetom duljine a=45cm . Izračunajte duljinu druge katete tog trokuta.
c=53cm
a=45cm
b=?
b2=c2-a2
b2=532-452
b2=784
b=√784=28cm
Duljina druge katete tog trokuta iznosi
28cm.
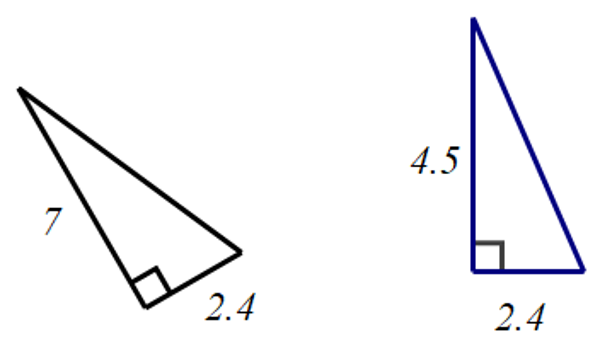
Izračunajte duljine nepoznatih stranica (duljine stranica izražene su u centimetrima).
Dodatno uvježbajte izračunavanje duljina nepoznatih stranica pravokutnog trokuta (duljine stranica izražene su u centimetrima).
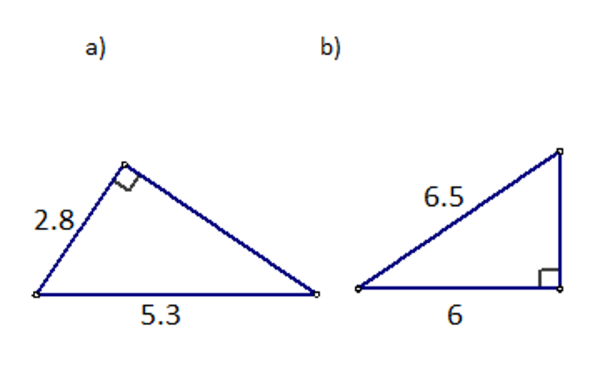
Izračunajte duljine nepoznatih stranica te opseg i površinu pravokutnih trokuta na slikama (svi su podatci zadani u centimetrima).
Neka je duljina nepoznate katete
a. Tada je
a2=5.32-2.82, iz čega slijedi da je
a2=20.25, tj.
a=√20.25=4.5cm.
Opseg trokuta jednak je zbroju duljina njegovih stranica te je
o=4.5+2.8+5.3=12.6cm.
Površina pravokutnog trokuta jednaka je polovini umnoška njegovih kateta te je p=4.5·2.82=6.3cm2.
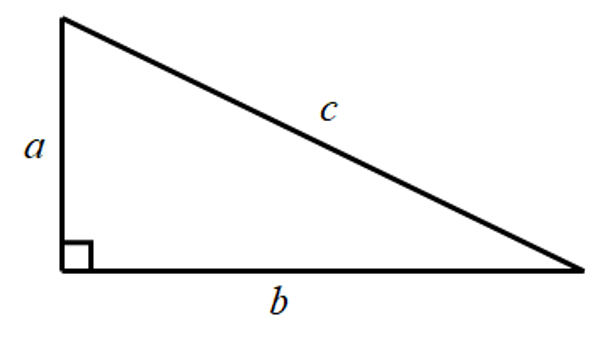
Prisjetimo se, za pravokutni trokut sa standardnim oznakama sa slike vrijedi:
p=a·b2.
Neka je duljina nepoznate katete
b. Tada je
b2=6.52-62, iz čega slijedi da je
b2=6.25, tj.
b=√6.25=2.5cm.
o=6+2.5+6.5=15cm
p=6·2.52=7.5cm2.
Trokut
EFG pravokutan je s pravim kutom pri vrhu
E, pri čemu je
|EF|=5cm i
|FG|=13cm. Izračunajte duljinu treće stranice tog trokuta.
Taj je zadatak rješavalo nekoliko učenika. Provjerite njihova rješenja. Ispravite rješenja koja nisu ispravna.
Markovo rješenje:
|EG|2=132-52=26-10=16cm.
Duljina stranice -EG iznosi 16cm.
Petrino rješenje:
|EG|2=132-52=82=64cm.
Duljina stranice
-EG iznosi
64cm.
Janovo rješenje:
|EG|2=132-52=169-25=144cm.
Duljina stranice -EG iznosi 72cm.
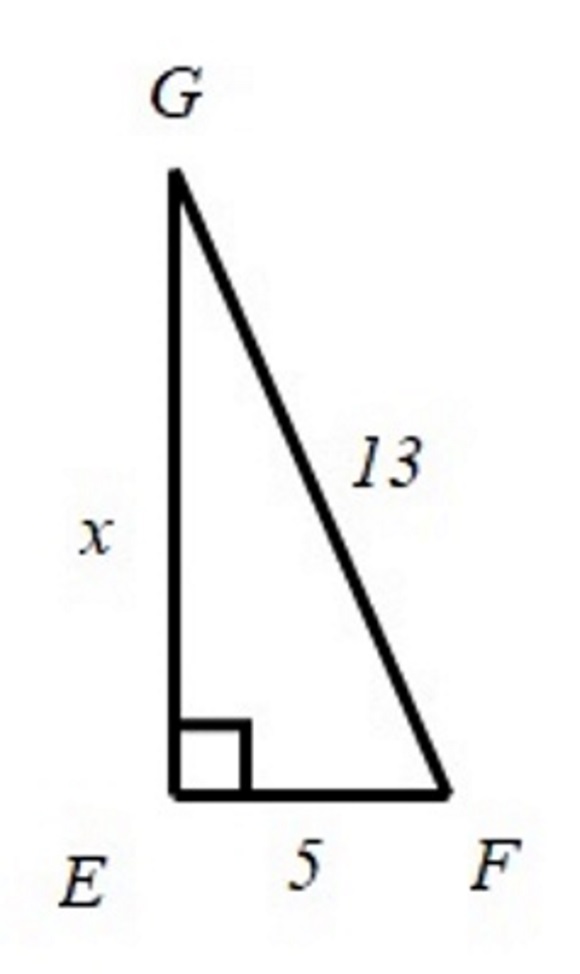
Sva su tri rješenja netočna.
Točno rješenje zadatka jest:
|EG|2=132-52=82=169-25=144cm
|EG|=√144=12cm.
Pitagorine trojke uređene su trojke prirodnih brojeva
(x,y,z) pri čemu su
x,y duljine kateta, a
z duljina hipotenuze pravokutnog trokuta, tj. vrijedi da je
x2+y2=z2
. Više o Pitagorinim trojkama pročitajte na stranicama Hrvatske enciklopedije.
Provjerite svoje znanje prije proučavanja složenijih zadataka.
Na odgovarajuća mjesta upišite preostale oznake stranica pravokutnog trokuta
n2-m2=o2.
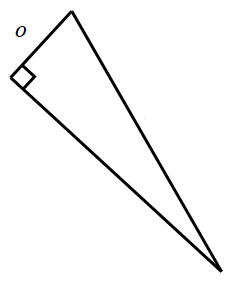
m
n
Ako su duljine kateta pravokutnog trokuta
2dm i
21cm, kolika je duljina njegove hipotenuze?
Duljina hipotenuze pravokutnog trokuta s katetama duljine
15cm i
36cm iznosi
39cm.
Postupak:
√152+362=39
Odredite duljinu stranice x ako su duljine svih stranica izražene u centimetrima.
Duljina hipotenuze pravokutnog trokuta sa stranicama
6cm i
8cm iznosi
c=√62+82=√100=10cm.
Duljina katete
x
drugoga pravokutnog trokuta iznosi
x=√142-102=√196-100=√96≈9.8cm.
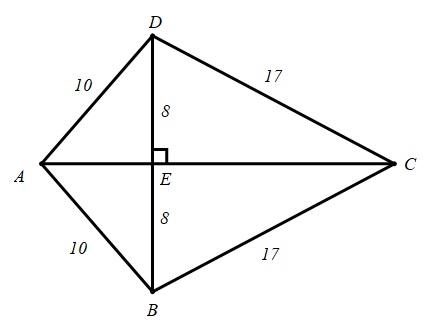
Nacrtan je četverokut kojemu su po dvije susjedne stranice jednakih duljina, a dijagonale međusobno okomite (deltoid).
Duljine njegovih stranica izražene su u centimetrima. Odredite duljinu dužine -AC.
Duljina stranice -AC jednaka je zbroju duljina stranica -AE i -EC.
|AE|=√102-82=√36=6cm
|EC|=√172-82=√225=15cm
Duljina stranice
-AC iznosi
6+15=21cm.
Izračunajte duljine nacrtanih dužina. Rezultat zaokružite na najbližu desetinku centimetra.
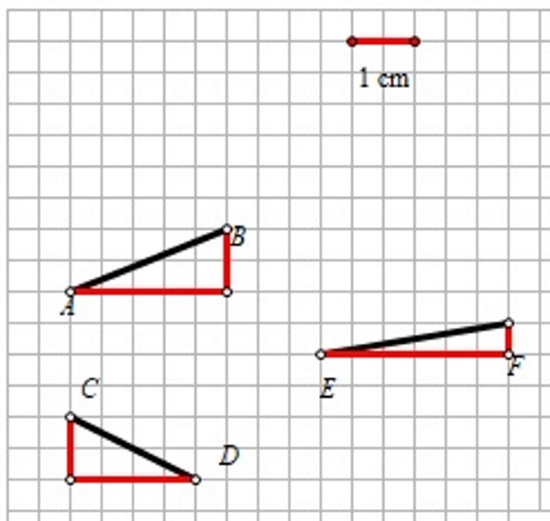
Ako docrtamo pravokutne trokute tako da zadane dužine budu hipotenuze, zadatke možemo riješiti primjenom Pitagorina poučka:
|AB|2=2.52+12
|AB|2=6.25+1=7.25
|AB|=√7.25≈2.7cm
ili kraće
|AB|=√2.52+12=√6.25+1=√7.25≈2.7cm
|CD|=√22+12=√4+1=√5≈2.2cm
|EF|=√32+0.52=√9+0.25=√9.25≈3.0cm.
Ako se drugi grad nalazi
24 kilometra istočno i
10 kilometara južno od prvoga grada, kolika je njihova zračna udaljenost?
Udaljenost gradova,
d, može se prikazati bilo kojim od prikazanih dvaju međusobno sukladnih pravokutnih trokuta.
d=√242+102=26km
Udaljenost između gradova iznosi 26 kilometara.
Određivanje udaljenosti dviju točaka možete uvježbati i s pomoću sljedeće aktivnosti.
Upišite koordinatu vrha
C trokuta
ABC kako bi dužina
-AB postala hipotenuza
pravokutnog trokuta te provjerite svoje rješenje.
Nakon što ste upisali točno rješenje, prikazat će vam se pravokutnici u koje trebate upisati duljine kateta a i b.
Nakon što točno upišete duljine kateta, prikazat će se novi pravokutnik. Izračunajte udaljenost točaka
A i
B, tj. duljinu hipotenuze tog trokuta pa je upišite u taj pravokutnik. Rješenja, prema potrebi, zaokružite na dvije decimale.
Ivona i njezina majka puštale su bespilotnu letjelicu po svojemu susjedstvu. Ivona je letjelicu pustila u zrak s raskrižja Ulice Ivana Trnskog i Ulice Ferde Livadića te je letjela putanjom ucrtanom crvenim linijama. Sletjela je na raskrižju Maksimirske ceste i Ulice Ferde Livadića. Koju je udaljenost prešla bespilotna letjelica?
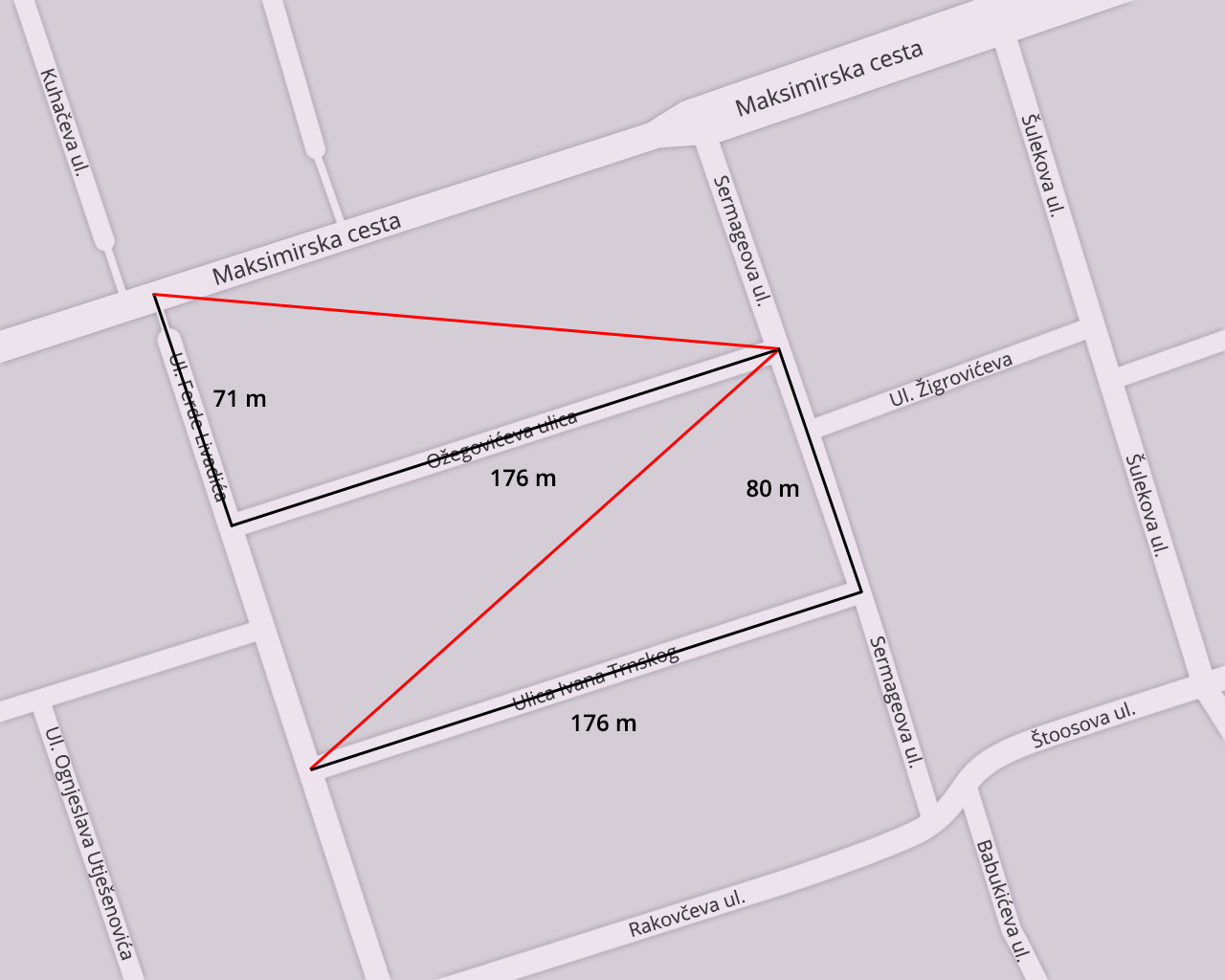
Duljina hipotenuze pravokutnog trokuta računa se primjenom Pitagorina poučka.
prvakateta2+drugakateta2=hipotenuza2
Duljina hipotenuze pravokutnog trokuta s katetama duljine
176m i
80m iznosi:
x2=1762+802
x2=37376
x≈193.33≈193m.
Duljina hipotenuze pravokutnog trokuta s katetama duljine 176m i 71m iznosi:
y2=1762+712
y2=36017
y≈189.78≈190m.
Ukupna udaljenost koju je prešla bespilotna letjelica iznosi približno:
193+190=383m.
Ljestve duljine
4m prislonjene su na zid. Udaljenost baze ljestava od zida iznosi
85cm. Do koje visine sežu ljestve? Rezultat zaokružite na najbliži centimetar.

Visina do koje dosežu ljestve jednaka je duljini druge katete pravokutnog trokuta sa zadane slike.
x=√4002-852≈391cm
Ljestve dosežu do visine otprilike
391cm.
Tiana je zalupila kućna vrata, a zaboravila je uzeti ključeve. Opazila je da je prozor na drugom katu kuće ostao otvoren. U garaži je pronašla ljestve duljine
4.5 metara. Ako je visina zida od tla do donjeg ruba prozora
3.5 metara, a udaljenost od baze kuće do baze ljestava
60cm, hoće li ljestve dosegnuti prozor?

Duljina ljestava potrebnih da dosegnu prozor treba biti
√3.52+0.62≈3.6m, zato su Tianine ljestve dovoljno dugačke da dosegnu prozor.
Duljine kateta pravokutnog trokuta iznose
√72cm i
(x-1)cm, a duljina hipotenuze
(x+5)cm. Odredite
x te duljine preostalih dviju stranica tog trokuta.
Za pravokutni trokut sa zadanim duljinama stranica vrijedi:
(x+5)2=√722+(x-1)2.
Nakon kvadriranja dobivamo:
x2+10x+25=x2-2x+1+√722.
Pojednostavnjivanjem dobivamo da je
10x+25=-2x+1+72.
Zato je
12x=48
x=4.
Duljina druge katete iznosi
x-1=4-1=3cm, a hipotenuze
x+5=4+5=9cm
.
Hipotenuza je od jedne katete pravokutnog trokuta dulja za 2cm. Duljina druge katete tog trokuta jest 12cm. Odredite opseg i površinu tog trokuta.
Neka je xduljina prve katete tog trokuta. Tada je x+2duljina hipotenuze. Tada vrijedi
(x+2)2=x2+122. Kvadriranjem obiju strana jednakosti dobivamo izraz
x2+4x+4=x2+144, a nakon pojednostavnjivanja izraz
4x+4=144. Iz toga slijedi da je
4x=140, tj.
x=35.
Duljine stranica toga trokuta jesu
12cm,
35cm i
37cm.
Opseg je tog trokuta
o=12+35+37=84cm.
Površina tog trokuta (p=prvakateta·drugakateta2) iznosi p=12·352=210cm2.
Duljine kateta pravokutnog trokuta odnose se kao
3:4. Kolike su duljine kateta tog trokuta ako je duljina hipotenuze
85cm?
Neka je a=3k i b=4k.
Tada vrijedi (3k)2+(4k)2=852. Iz toga slijedi da je 9k2+16k2=7225.
Zato je 25k2=7225 i k2=289, odnosno k=17.
Dakle, a=3·17=51cm i b=4·17=68cm.
Možda ste iz omjera zamijetili da se radi o egipatskom trokutu kojemu su stranice u omjeru 3:4:5. S obzirom na to da je duljina hipotenuze uvećana 17 puta, i duljine kateta bit će uvećane isti broj puta. Zato je duljina jedne katete 51cm, a druge 68cm.
Omjer kateta pravokutnog trokuta
ABC s pravim kutom pri vrhu
C jest
20:21. Odredite duljine njegovih stranica ako je opseg tog trokuta
210mm.
Neka je
a=20k i
b=21k.
Iz Pitagorina poučka slijedi da je
c2=(20k)2+(21k)2, odnosno
c2=400k2+441k2.
Duljina hipotenuze jest
c=√841k2=29k.
Iz formule za opseg dobivamo da je
20k+21k+29k=210, tj.
k=3.
Duljine stranica su zato
a=20k=20·3=60cm i
b=21k=21·3=63cm i
c=29k=29·3=87cm.
U ovoj ste jedinici naučili:
Za kraj pogledajte videozapis u kojem je prikazan origami dokaz Pitagorina poučka te procijenite svoje znanje.
Ako je duljina jedne katete 99mm, a druge 20mm, tada je duljina hipotenuze 101mm.
Postupak:
√992+202=√10201=101
Ako je duljina hipotenuze
15cm, a duljina jedne katete pravokutnog trokuta
8cm, kolika je duljina druge katete tog trokuta?
Postupak:
√152-82=√161

Postupak:
Duljina mosta =2·√562-482≈58m
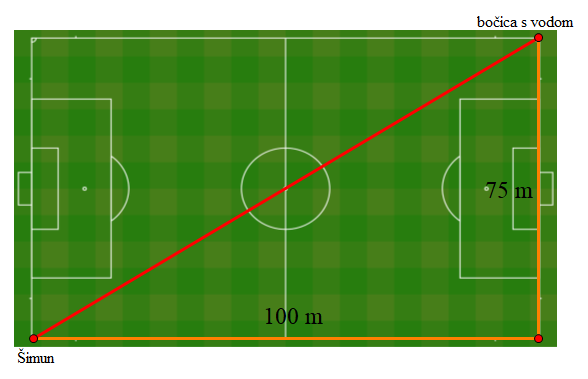
Postupak:
(100+75)-√1002+752=175-125=50