Brojevni pravac

Brojevni pravac je

na kojem su prikazani

. Uzastopni cijeli brojevi međusobno su

udaljeni jedan od drugog.

pravac

jednako

brojevi

Pomoć:

Zamisli da je cesta pravac, a stanice uzastopni cijeli brojevi.

null

Točku s brojem $0$ označimo slovom $O,$ a točku s brojem $1$ označimo slovom $E,$ kao na slici.

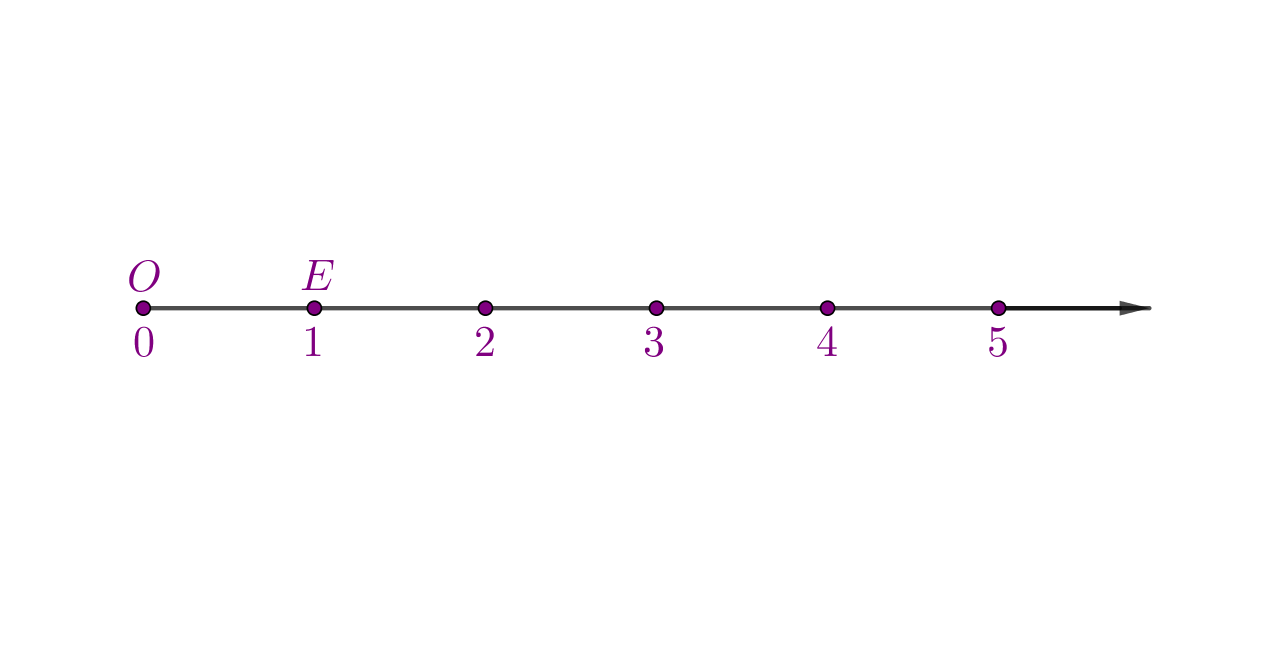
Brojevni pravac s označenim točkama O i E. Točka O nalazi se na prvoj točkici iznad crte s lijeve strane, a točka E na drugoj točkici iznad crte s lijeve strane. — Brojevni pravac s označenim točkama O i E

Pridruživanje brojeva točkama pravca zapisujemo kao $O (0)$ i $E (1) .$ U tom zapisu broj $0$ nazivamo koordinata točke $O,$ a broj $1$ nazivamo koordinata točke $E .$

Zanimljivost

Riječ koordinata dolazi od latinske riječi coordinare što znači uskladiti.

Točka $O (0)$ je

točka brojevnog pravca. Točka

je odabrana točka na

koja slijedi neposredno nakon točke

$O (0) .$

brojevnom pravcu

$E (1)$

početna

Pomoć:

Razmisli i pogledaj slike brojevnih pravaca.

null

Ishodište i jedinična točka brojevnog pravca

Točku $O (0)$ zovemo ishodište, a točku $E (1)$ jedinična točka brojevnog pravca.

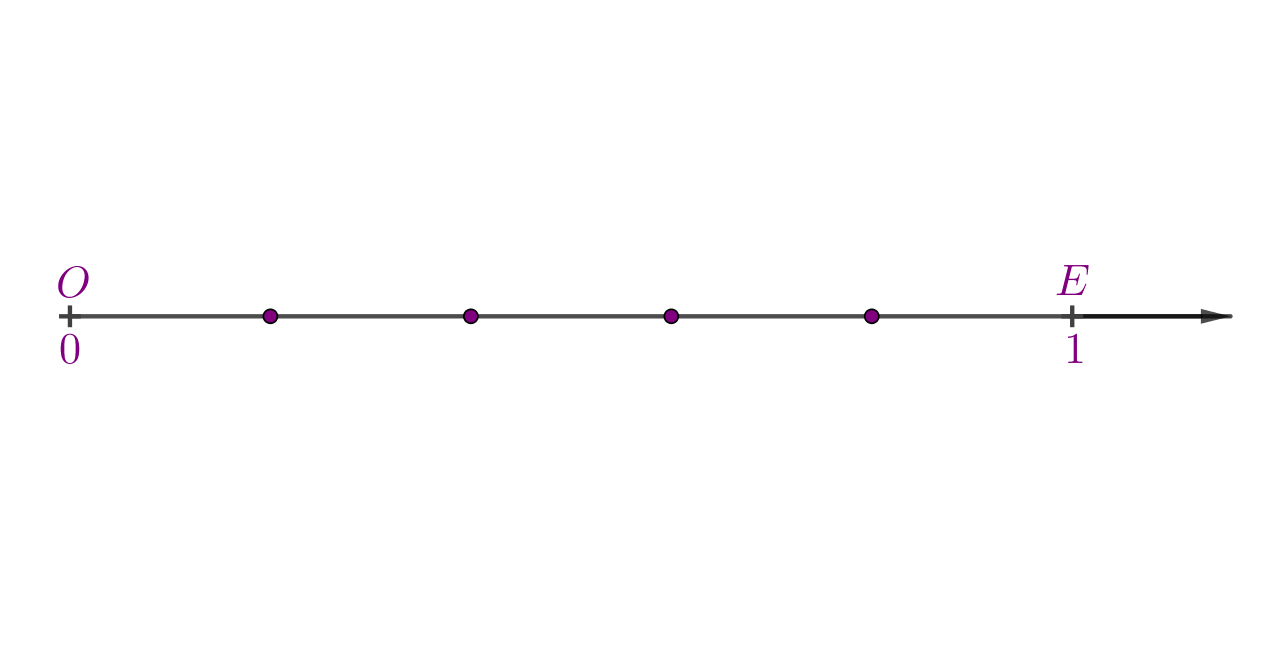
Duljina dužine $\bar{O E}$

međusobnu

udaljenost uzastopnih cijelih brojeva na zadanom brojevnom pravcu.

Pomoć:

Razmisli i pogledaj slike brojevnih pravaca.

null

Jedinična dužina

Dužinu $\bar{O E}$ nazivamo jediničnom dužinom. Duljinu jedinične dužine označavamo $|O E| .$ Duljina jedinične dužine označava udaljenost uzastopnih cijelih brojeva na zadanom brojevnom pravcu. Odabirom ishodišta i jedinične dužine kažemo da smo organizirali brojevni pravac ili koordinatni sustav na pravcu.

Zadatak 1.

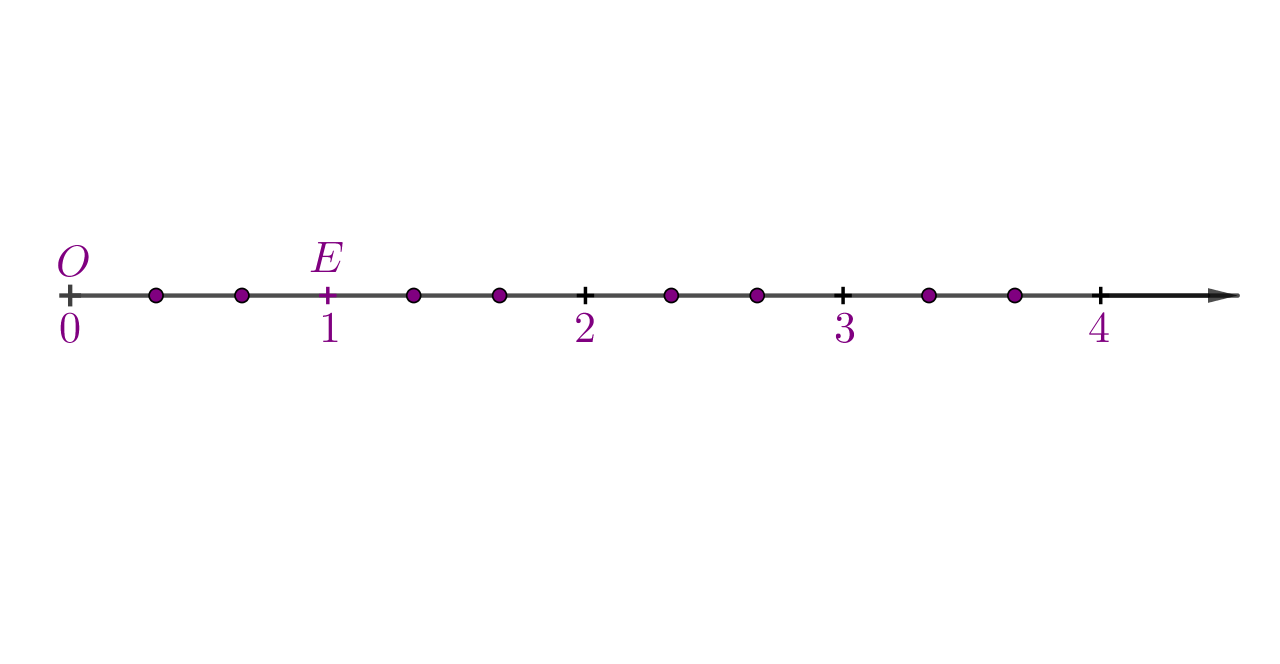
Na brojevnom pravcu zadane jedinične dužine $\bar{O E}$ upiši točku $A$ tako da bude pridružena broju $2,$ točku $B$ da bude pridružena broju $4$ i točku $C$ tako da bude pridružena broju $7 .$

Brojevni pravac na kojem su označeni ishodište i jedinična dužina

$A$

$2$

$B$

$4$

$C$

$7$

Pomoć:

Broj zapiši ispod označene točke na pravcu, a slovo iznad točke na pravcu.

Postupak:

Pazi da ostaviš prazna mjesta za neoznačene cijele brojeve.

Pridruživanje brojeva točkama pravca zapisujemo kao $A ($

$),$

$B ($

$),$

$C ($

$) .$

Pomoć:

U zagradu zapiši broj koji je pridružen točkama pravca kako je zadano u tekstu zadatka.

Koordinata točke

Ako je nekom broju $x$ pridružena točka $T$ na brojevnom pravcu, to zapisujemo kao $T (x) .$ Broj $x$ je koordinata točke $T .$

Zadatak 2.

Odredi koordinate točaka

$A,$

$B,$

$C$ i

$D$ sa slike. Spoji parove.

Na brojevnom pravcu su označeni O, E i nazivi točaka A, B, C i D

$C$	$(6)$
$A$	$(9)$
$B$	$(3)$
$D$	$(4)$

Pomoć:

Dobro pogledaj brojevni pravac na slici.

null

Osim cijelih brojeva, točkama brojevnog pravca možemo pridružiti i razlomke.

Razlomci jednakih nazivnika na brojevnom pravcu

Zadatak 3.

Ako dugački kruh "francuz" prerežemo s četiri reza, dobit ćemo

dijelova,

odnosno komada kruha.

Pomoć:

Zamisli ili uzmi kruh i reci nekom odraslom da ga prereže s četiri reza. Prebroji komade kruha.

null

Jediničnu dužinu na slici podijelili smo na

jednakih

dijelova. Svaki taj dio je

jedinične

duljine.

Pomoć:

Kada cjelinu dijelimo na $5$ jednakih dijelova, dobivamo petine.

null

Pridruži razlomke točkama pravca.

Jedinična dužina podijeljena na pet jednakih dijelova.

$\frac{3}{5}$

$\frac{2}{5}$

$\frac{4}{5}$

$\frac{1}{5}$

Pomoć:

Pogledaj brojevni pravac i razmisli na koliko je dijelova podijeljena jedinična dužina.

null

Zadatak 4.

Odredi najbliže cijele brojeve između kojih se nalaze zadani razlomci. Spoji parove.

$2 \frac{1}{3}$	Između $0$ i $1$
$\frac{10}{3}$	Između $1$ i $2$
$\frac{5}{3}$	Između $2$ i $3$
$\frac{2}{3}$	Između $3$ i $4$

Pomoć:

Svaki nepravi razlomak zapiši u obliku mješovitog broja, dobro ga pročitaj i razmisli. Pravi razlomak nalazi se između $0$ i $1 .$

Postupak:

$\frac{10}{3} = 3 \frac{1}{3}$

$\frac{5}{3} = 1 \frac{2}{3}$

Ucrtaj na brojevni pravac točke $A (2 \frac{1}{3}),$ $B (\frac{10}{3}),$ $C (\frac{2}{3})$ i $D (\frac{5}{3}) .$

Brojevni pravac od 0 do 4 s označenim trećinama Slovo O nalazi se na prvoj točkici iznad crte s lijeve strane (ispod je 0). Slovo E nalazi se na četvrtoj točkici s lijeve strane (ispod je 1). Broj 2 nalazi se na sedmoj točkici s lijeve strane. Broj 3 nalazi se na desetoj točkici s lijeve strane i broj 4 je na trinaestoj točkici.

$A$

$B$

$C$

$D$

$2 \frac{1}{3}$

$\frac{10}{3}$

$\frac{2}{3}$

$\frac{5}{3}$

Pomoć:

Ispod točke na brojevnom pravcu upiši koordinatu (broj), iznad upiši ime točke (slovo).

Postupak:

Razlomak zapiši u obliku mješovitog broja.

Zadatak 5.

Odredi koordinate točaka $A,$ $B,$ $C$ i $D$ sa slike. Spoji parove.

Na brojevnom pravcu od 0 do 3 označene su četvrtine i točke A, B, C i D. A se nalazi između 0i 1. B se nalazi između 1 i 2 (bliže broju

$D$	$(\frac{7}{4})$
$A$	$(\frac{11}{4})$
$B$	$(\frac{1}{2})$
$C$	$(\frac{9}{4})$

Pomoć:

Najprije koordinatu zapiši kao mješoviti broj s nazivnikom $4$ . Razlomak skrati do kraja. Mješoviti broj zapiši u obliku razlomka.

Postupak:

$\frac{2}{4} = \frac{1}{2}$

$1 \frac{3}{4} = \frac{7}{4}$

$2 \frac{1}{4} = \frac{9}{4}$

$2 \frac{3}{4} = \frac{11}{4}$

Ako razlomci nemaju jednake nazivnike, svedemo ih na najmanji zajednički nazivnik.

Razlomci na brojevnom pravcu

Primjer 1.

Ucrtaj na brojevni pravac točke $A (\frac{3}{2}),$ $B (2 \frac{1}{2}),$ $C (\frac{2}{3})$ i $D (\frac{11}{6})$ . Zadatak pokušaj riješiti samostalno u bilježnicu, zatim provjeri svoje rješenje.

Najmanji zajednički nazivnik je $V (2, 3, 6) = 6 .$ Razlomke, koje treba, zapišemo u obliku mješovitog broja da bismo mogli lakše odrediti između kojih se najbližih cijelih brojeva nalaze. Nakon toga ih svedemo na najmanji zajednički nazivnik.

$\frac{3}{2} = 1 \frac{1}{2} = 1 \frac{3}{6},$ $2 \frac{1}{2} = 2 \frac{3}{6},$ $\frac{2}{3} = \frac{4}{6},$ $\frac{11}{6} = 1 \frac{5}{6} .$

Zatim te brojeve ucrtamo na brojevni pravac. Jediničnu dužinu podijelimo na šest jednakih dijelova, odnosno na šestine. Točku $A$ ucrtamo između $1$ i $2$ na trećoj šestini brojeći od $1,$ točku $B$ ucrtamo između $2$ i $3$ na trećoj šestini brojeći od $2,$ točku $C$ ucrtamo između $0$ i $1$ na četvrtoj šestini brojeći od $0$ i točku $D$ ucrtamo između $1$ i $2$ na petoj šestini brojeći od $1 .$ Na brojevni pravac zapišemo koordinate koje su zadane u zadatku.

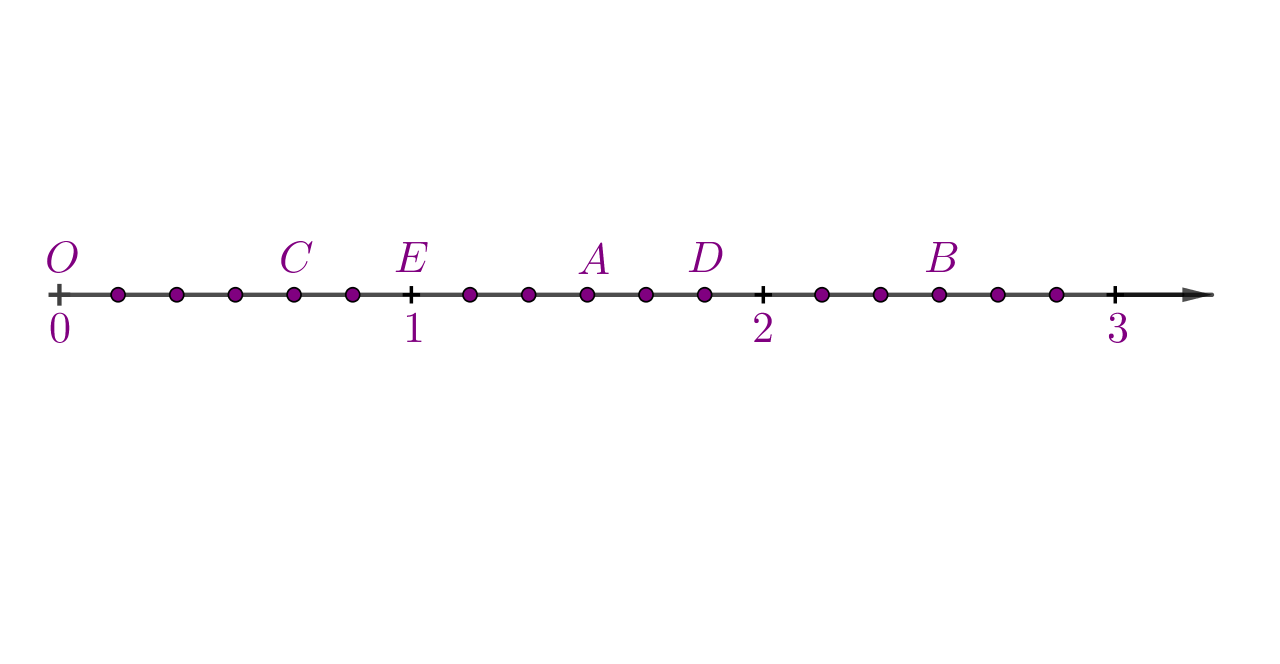
Na brojevnom pravcu od 0 do 3 ucrtane su šestine i točke A, B, C i D. — Razlomci na brojevnom pravcu

Zadatak 6.

Ucrtaj na brojevni pravac točke $A (\frac{11}{8}),$ $B (\frac{1}{2}),$ $C (\frac{7}{8})$ i $D (\frac{7}{4}) .$

Točka $A$ nalazi se između

,

točka

$B$ nalazi se između

,

točka

$C$ nalazi se između

,

točka

$D$ nalazi se između

.

Pomoć:

Koordinate točaka zapiši u obliku mješovitog broja.

Postupak:

$\frac{11}{8} = 1 \frac{3}{8}$

$\frac{7}{4} = 1 \frac{3}{4}$

Najmanji zajednički nazivnik razlomaka u zadatku je:

$4$

Razmisli ponovo ili pogledaj uputu.

$6$

Razmisli ponovo ili pogledaj uputu.

$8$

Bravo!

$2$

Razmisli ponovo ili pogledaj uputu.

Pomoć:

Izračunaj najmanji zajednički višekratnik svih nazivnika u zadatku.

Postupak:

$V (2, 4, 8) = 8$

Jediničnu dužinu podijelimo na

.

Pomoć:

Jediničnu dužinu poodijelimo na onoliko dijelova koliki je najmanji zajednički nazivnik svih razlomaka u zadatku.

Postupak:

$V (2, 4, 8) = 8$

Povuci točke i njihove koordinate na brojevni pravac.

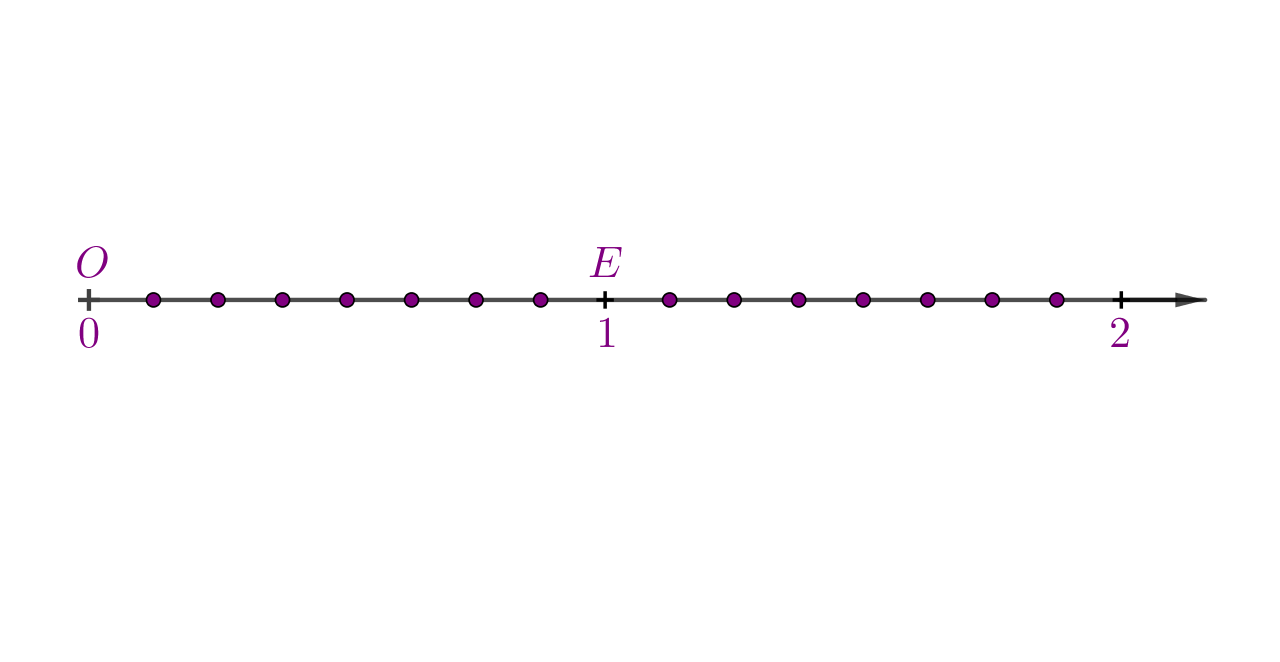
Brojevni pravac od 0 do 2 na kojem su označene osmine i točke A, B, C i D.

$A$

$B$

$C$

$D$

$\frac{11}{8}$

$\frac{1}{2}$

$\frac{7}{4}$

$\frac{7}{8}$

Pomoć:

Iznad brojevnog pravca stavi ime točke (slovo), a ispod brojevnog pravca stavi njenu koordinatu (broj).

Postupak:

$A (\frac{11}{8})$ smjesti između $1$ i $2$ na treću osminu od $1,$ $B (\frac{1}{2})$ smjesti između $0$ i $1$ na četvrtu osminu od $0,$ $C (\frac{7}{8})$ smjesti između $0$ i $1$ na sedmu osminu od $0$ i $D (\frac{7}{4})$ smjesti između $1$ i $2$ na šestu osminu od $1 .$

Zadatak 7.

Ucrtaj točke $A (\frac{3}{2}),$ $B (\frac{8}{3}),$ $C (2 \frac{1}{6})$ i $D (\frac{5}{4})$ na brojevni pravac. Zadatak pokušaj riješiti samostalno u bilježnicu, a zatim provjeri svoje rješenje.

Jediničnu dužinu podijeli na dvanaestine jer je

$V (2, 3, 4, 6) = 12 .$ Razlomke zapiši u obliku mješovitog broja i svedi na najmanji zajednički nazivnik. Uoči da su sve točke smještene između

$1$ i

$3$ na brojevnom pravcu. U tom slučaju, brojevni pravac ne trebaš crtati od nule, dovoljno je nacrtati dio brojevnog pravca od

$1$ do

$3$ radi bolje preglednosti.

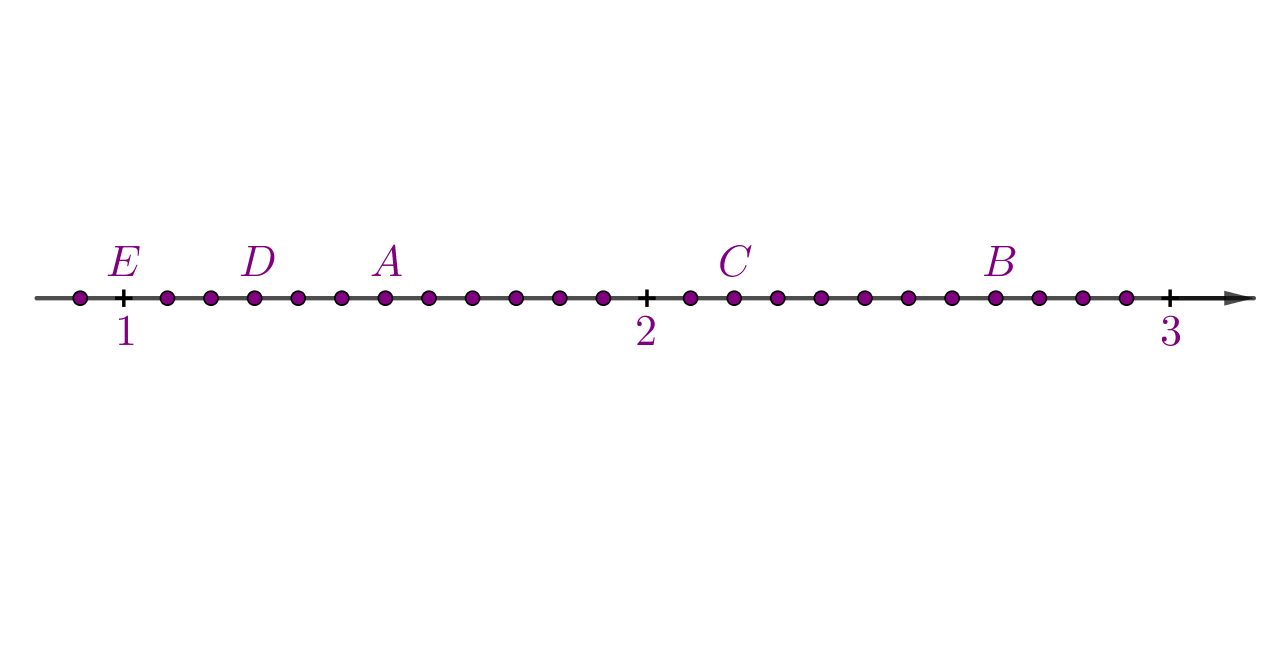
Brojevni pravac od 1 do 3 kome su ucrtane dvanaestine te točke A, B, C, D i njihove koordinate — Razlomci na brojevnom pravcu

Zadatak 8.

Odredi koordinate točaka sa slike. Spoji parove.

Brojevni pravac na kojem je jedinična dužina podijeljena na šestine i ucrtane točke P, L, A i N. Slovo P je na drugoj točkici od broja 4. Slovo L je na petoj točkici od broja 4. Slovo A je na trećoj točkici od broja 5. Slovo N je na četvrtoj točkici od broj 5.

$L$	$(\frac{17}{3})$
$A$	$(\frac{29}{6})$
$N$	$(\frac{13}{3})$
$P$	$(\frac{11}{2})$

Pomoć:

Uočit ćeš da je jedinična dužina podijeljena na šestine i da su svi brojevi između $4$ i $6 .$ Ucrtane koordinate zapiši u obliku mješovitog broja s nazivnikom $6$ , zatim skrati do kraja i zapiši u obliku nepravog razlomka.

Postupak:

$4 \frac{2}{6} = 4 \frac{1}{3} = \frac{13}{3}$

$4 \frac{5}{6} = \frac{29}{6}$

$5 \frac{3}{6} = 5 \frac{1}{2} = \frac{11}{2}$

$5 \frac{4}{6} = 5 \frac{2}{3} = \frac{17}{3}$

Decimalni brojevi na brojevnom pravcu

Primjer 2.

Ucrtaj na brojevni pravac točke $A (5.6),$ $B (0.4),$ $C (6.7),$ $D (8.2)$ i $F (3.5) .$ Zadatak pokušaj riješiti samostalno u bilježnicu, a zatim provjeri svoje rješenje.

U bilježnici je najlakše uzeti $10 mm$ za jediničnu dužinu, tada je desetina jedinične dužine $1 mm .$ Točka $A$ je udaljena $6 mm$ ( $6$ desetina) od broja $5,$ točka $B$ je udaljena $4 mm$ ( $4$ desetine) od nule, točka $C$ je udaljena $7 mm$ ( $7$ desetina) od broja $6,$ točka $D$ je udaljena $2 mm$ ( $2$ desetine) od broja $8$ i točka $F$ je udaljena $5 mm$ ( $5$ desetina) od broja $3 .$

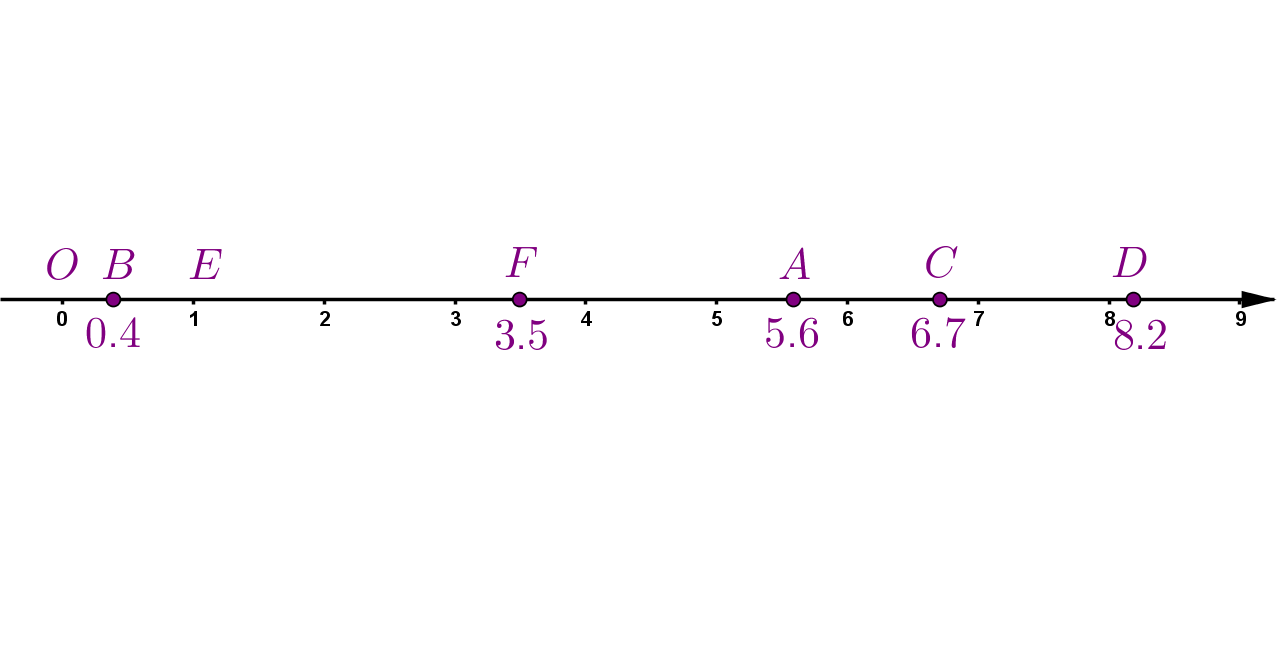
Brojevni pravac kome je jedinična dužina podijeljena na desetine, sa ucrtanim točkama A, B, C, D i F. — Decimalni brojevi na brojevnom pravcu

Ako decimalni brojevi imaju više decimala, možemo ih zaokružiti na jednu decimalu. Ako su brojevi jako blizu i brojevni pravac s jediničnom dužinom duljine $10 mm$ je nepregledan, za duljinu jedinične dužine možemo uzeti $10 cm$ , a decimalne brojeve zaokružiti na dvije decimale.

Zadatak 9.

Smjesti decimalne brojeve na pravo mjesto na brojevnom pravcu.

Brojevni pravac od 0 do 6 s označenim poljima za decimalne brojeve.

$3.6$

$0.75$

$5.82$

$2.25$

$4.5$

Pomoć:

Razmisli između kojih se najbližih cijelih brojeva nalazi zadani decimalni broj.

Zadatak 10.

Odredi koordinate točaka na brojevnom pravcu sa slike. Spoji parove.

Brojevni pravac od 2 do 6 sa ucrtanim točkama T, I, G, A, R. Slovo T nalazi se između brojeva 2 i 3. Slova I i G nalaze se između brojeva 3 i 4. Slova A i R nalaze se između brojeva 4 i 5.

$T$	$(3.31)$
$R$	$(2.7)$
$G$	$(4.85)$
$I$	$(4.5)$
$A$	$(3.5)$

Pomoć:

Odredi između kojih se najbližih cijelih brojeva nalazi zadani decimalni broj. Za brojeve, koji se nalaze između istih cijelih brojeva, odredi koji je broj manji.

Postupak:

$2.7$ je između $2$ i $3,$ $3.5$ i $3.31$ su oba između $3$ i $4,$ ali je $3.31 < 3.5,$ $4.5$ i $4.85$ su oba između $4$ i $5,$ ali je $4.5 < 4.85 .$

Ako razlomci, koje želimo smjestiti na brojevni pravac, imaju preveliki zajednički nazivnik, zapišemo ih u obliku decimalnih brojeva, zaokružimo na jednu ili dvije decimale i tako smjestimo na brojevni pravac.

Praktična vježba

Podijelite se u razredu u grupe po troje ili četvero. Svatko neka zapiše na papirić (da drugi ne vide) jedan ili dva pozitivna racionalna broja. Otkrijte papiriće i ucrtajte brojeve na brojevni pravac. Odigrajte nekoliko krugova i napravite izložbu tako dobivenih brojevnih pravaca na razrednom panou.

Kutak za znatiželjne

Polovište dužine

Pokušaj samostalno riješiti sljedeće zadatke i zaključiti kako bi izračunali koordinatu polovišta dužine na brojevnom pravcu.

Koordinata točke $A$ na brojevnom pravcu koja je jednako udaljena od točaka $P (3)$ i $S (4)$ je $A ($

$) .$

Pomoć:

Nacrtaj u bilježnicu brojevni pravac i na njemu označi točke $P (3)$ i $S (4)$ te razmisli gdje se nalazi točka koja je jednako udaljena od točaka $P$ i $S .$

Rješenje izraza

$(3 + 4) : 2$ je

Rješenje zapiši kao decimalni broj s decimalnom točkom ili pogledaj uputu.

.

Pomoć:

Zadatak riješi poštujući redoslijed računskih radnji.

Koordinata točke $R$ na brojevnom pravcu koja je jednako udaljena od točaka $B (2.8)$ i $K (3.6)$ je $R ($

$) .$

Pomoć:

Nacrtaj u bilježnicu brojevni pravac i na njemu označi točke $B (2.8)$ i $K (3.6)$ te razmisli gdje se nalazi točka koja je jednako udaljena od točaka $B$ i $K .$

Rješenje izraza

$(2.8 + 3.6) : 2$ je

Rješenje zapiši u obliku decimalnog broja s decimalnom točkom ili pogledaj uputu.

.

Pomoć:

Zadatak riješi poštujući redoslijed računskih radnji.

Koordinata točke $I$ na brojevnom pravcu koja je jednako udaljena od točaka $K (2 \frac{3}{4})$ i $T (3 \frac{1}{4})$ je $I ($

$) .$

Pomoć:

Nacrtaj u bilježnicu brojevni pravac i na njemu označi točke $K (2 \frac{3}{4})$ i $T (3 \frac{1}{4})$ te razmisli gdje se nalazi točka koja je jednako udaljena od točaka $K$ i $T .$

Rješenje izraza

$(2 \frac{3}{4} + 3 \frac{1}{4}) : 2$ je

Rješenje zapiši u obliku decimalnog broja s decimalnom točkom ili pogledaj uputu.

.

Pomoć:

Zadatak riješi poštujući redoslijed računskih radnji.

Zaključimo.

Polovište dužine na brojevnom pravcu

Polovište dužine je točka na dužini koja je jednako udaljena od rubnih točaka te dužine. Neka rubne točke dužine $\bar{A B}$ imaju koordinate $A (x_{A})$ i $B (x_{B}) .$ Koordinatu polovišta $P (x_{P})$ dobijemo tako da izračunamo izraz $x_{P} = (x_{A} + x_{B}) : 2$ što možemo zapisati i u obliku razlomka $x_{P} = \frac{x_{A} + x_{B}}{2} .$

Zadatak 11.

Zadane su koordinate točaka $A$ i $B$ na brojevnom pravcu. Izračunaj koordinate polovišta $P$ dužine $\bar{A B} .$ Spoji parove.

$A (3 \frac{5}{6}),$ $B (\frac{29}{4})$	$P (4 \frac{5}{16})$
$A (\frac{15}{8}),$ $B (6 \frac{3}{4})$	$P (4 \frac{19}{20})$
$A (3.8),$ $B (\frac{28}{5})$	$P (5 \frac{13}{24})$
$A (3 \frac{1}{2}),$ $B (6.4)$	$P (4.7)$

Pomoć:

Nacrtaj u bilježnicu brojevne pravce i zadane točke. Izračunaj koordinate polovišta po formuli. Provjeri dobiveno rješenje na brojevnom pravcu.

Postupak:

Koordinate točaka $A$ i $B$ zapiši u obliku razlomka. Zbroji ih i dobiveno rješenje podijeli s $2 .$ Ili drugi način: uvrsti koordinate točaka $A$ i $B$ u formulu kao dvojni razlomak i riješi ga. Konačno rješenje zapiši u obliku mješovitog ili decimalnog broja.

...i na kraju

Ponovimo brojevni pravac kratkom procjenom znanja.

Procijenite svoje znanje

Točka $O (0)$ je

, točka

$E (1)$ je

, a dužina

$\bar{O E}$ je

brojevnog pravca. Odabirom ishodišta i jedinične točke kažemo da smo organizirali

.

brojevni pravac

jedinična točka

jedinična dužina

ishodište

Pomoć:

Dobro razmisli i dopuni rečenicu.

Odredi položaj točke u odnosu na najbliže cijele brojeve na brojevnom pravcu.

Točka $A (\frac{13}{4})$ nalazi se na brojevnom pravcu između cijelih brojeva
Točka $B (\frac{13}{2})$ nalazi se na brojevnom pravcu između cijelih brojeva
Točka $C (\frac{13}{14})$ nalazi se na brojevnom pravcu između cijelih brojeva
Točka $D (\frac{13}{8})$ nalazi se na brojevnom pravcu između cijelih brojeva

Pomoć:

Razlomke zapiši u obliku mješovitog broja i spoji parove.

Postupak:

$\frac{13}{2} = 6 \frac{1}{2}$

$\frac{13}{4} = 3 \frac{1}{4}$

$\frac{13}{8} = 1 \frac{5}{8}$

$\frac{13}{14} < 1$

Odredi koordinate točaka brojevnog pravca sa slike. Spoji parove.

Brojevni pravac od 3 do 5 podijeljen na šestine s točkama P, A, R, K. Slovo P nalazi se na trećoj točkici od broja 3. Slovo A nalazi se na petoj točkici od broja 3. Slovo R nalazi se na drugoj točkici od broja 4. Slovo K nalazi se na četvrtoj točkici od broja 4.

$A$	$(\frac{13}{3})$
$P$	$(\frac{7}{2})$
$R$	$(\frac{14}{3})$
$K$	$(\frac{23}{6})$

Pomoć:

Koordinate zapiši u obliku mješovitog broja s nazivnikom $6,$ skrati do kraja i zapiši u obliku razlomka.

Postupak:

$3 \frac{3}{6} = 3 \frac{1}{2} = \frac{7}{2}$

$3 \frac{5}{6} = \frac{23}{6}$

$4 \frac{2}{6} = 4 \frac{1}{3} = \frac{13}{3}$

$4 \frac{4}{6} = 4 \frac{2}{3} = \frac{14}{3}$

Smjesti točke $A (\frac{3}{2}),$ $B (2 \frac{1}{4}),$ $C (\frac{11}{4})$ i $D (0.75)$ na brojevni pravac.

Brojevni pravac od 0 do 3 podijeljen na četvrtine

$A$

$\frac{3}{2}$

$B$

$2 \frac{1}{4}$

$C$

$\frac{11}{4}$

$D$

$0.75$

Pomoć:

Koordinate točaka zapiši u obliku mješovitog broja i odredi između kojih cijelih brojeva se nalaze. Nalaze li se između istih cijelih brojeva, usporedi ih. Brojeve zapiši ispod brojevnog pravca, a imena točaka (slova) iznad brojevnog pravca.

Postupak:

$\frac{3}{2} = 1 \frac{1}{2}$

$\frac{11}{4} = 2 \frac{3}{4}$

$0.75 = \frac{3}{4} < 1$

$2 \frac{1}{4} < 2 \frac{3}{4}$

Povuci decimalni broj na njegovo mjesto na brojevnom pravcu.

Brojevni pravac od 8 do 13, na kojem su označena polja za decimalne brojeve

$12.9$

$8.15$

$12.21$

$8.7$

$10.5$

Pomoć:

Dobro pogledaj između kojih se najbližih cijelih brojeva nalazi zadani decimalni broj. Ako se decimalni brojevi nalaze između istih cijelih brojeva, usporedi ih.

Postupak:

$8.15 < 8.7$

$12.21 < 12.9$

6.1 Razlomci na brojevnom pravcu

Na početku...

Brojevni pravac

Zanimljivost

Ishodište i jedinična točka brojevnog pravca

Jedinična dužina

Zadatak 1.

Koordinata točke

Zadatak 2.

Razlomci jednakih nazivnika na brojevnom pravcu

Zadatak 3.

Zadatak 4.

Zadatak 5.

Razlomci na brojevnom pravcu

Primjer 1.

Zadatak 6.

Zadatak 7.

Zadatak 8.

Decimalni brojevi na brojevnom pravcu

Primjer 2.

Zadatak 9.

Zadatak 10.

Praktična vježba

Kutak za znatiželjne

Polovište dužine

Polovište dužine na brojevnom pravcu

Zadatak 11.

...i na kraju

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: