

Što uočavaš na animaciji? Zašto su djevojčice mislile kako sjede na istom mjestu? U čemu se njihova mjesta razlikuju?
Ponekad, kao u videu, brojevi dolaze u paru u kome se razlikuje koji je prvi, a koji drugi član para. Primjerice, kada tražimo svoje mjesto u kinu ili kazalištu i kad nam je važno razlikovati broj reda i broj sjedala.
Par brojeva, kod kojih se točno zna koji je prvi, a koji drugi član naziva se uređeni par. Označava se s Broj naziva se prvim, a drugim članom uređenog para.
Uređenim parom određuje se položaj nekog objekta. U animaciji je to bilo sjedalo u kinu, ali to može biti i, primjerice, položaj neke zgrade na karti grada ili položaj nekog grada na zemljovidu. Isto tako, uređenim parovima služe se i tvorci računalnih igrica kako bi pokazali položaj nekog lika iz igrice. Možeš li se i ti prisjetiti nekog uređenog para u svojoj okolini?
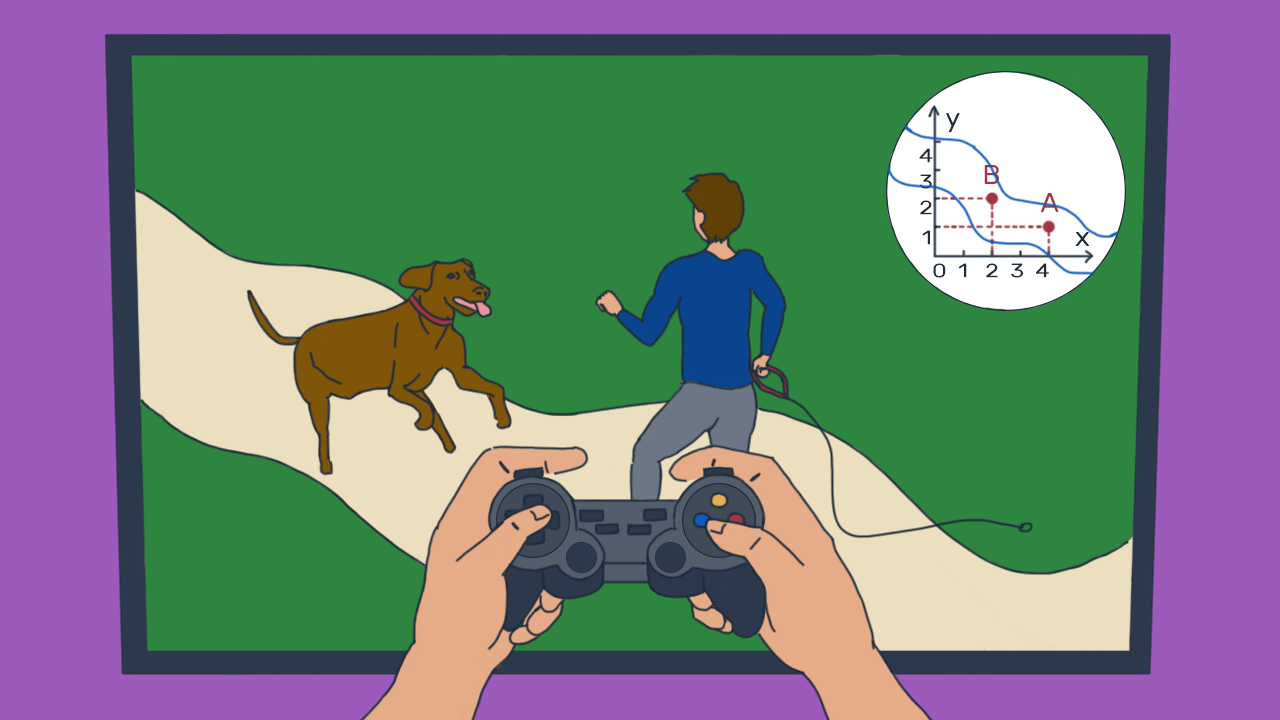
Istražimo
Pogledaj zemljopisnu kartu. Kako se određuje položaj na karti? Što znači geografska širina, a što geografska dužina? Poveži položaj na karti u geografiji s uređenim parovima u matematici.
Primjer 1.
Napiši sve uređene parove koji se mogu sastaviti od brojeva i
Dan je par brojeva
i
Da bi on postao uređeni par, moramo odrediti koji je prvi, a koji drugi član uređenog para. Razlikujemo uređeni par
i
Kako nije jasno određeno da u uređenom paru moraju biti oba broja, pomoću brojeva
i
mogu se sastaviti i uređeni parovi
i
Uočit ćeš kako uređeni parovi iz prošlih zadataka nisu jednaki. No, niti uređeni parovi iz početne animacije nisu jednaki, iako se na prvi pogled čine jednaki. Što misliš, kada su dva uređena para jednaka?
Dva uređena para su jednaka ako je prvi član jednak u oba uređena para i ako je drugi član jednak u oba uređena para.
Odnosno:
Upari jednake uređene parove.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Prisjeti se kada su dva uređena para jednaka!
Primjer 2.
Odredi nepoznati broj za koji vrijedi
Da bi uređeni parovi
i
bili jednaki, mora im biti jednak prvi član i mora im biti jednak drugi član. Prvi član im je jednak:
Kako i drugi član mora biti jednak, vrijedi:
Uređeni par je par brojeva kod kojega se točno zna koji je prvi, a koji drugi član. Dva uređena para su jednaka ako su im jednaki prvi članovi i ako su im jednaki drugi članovi.
Pogledaj crtež, pročitaj matematičku priču i odgovori na pitanja.
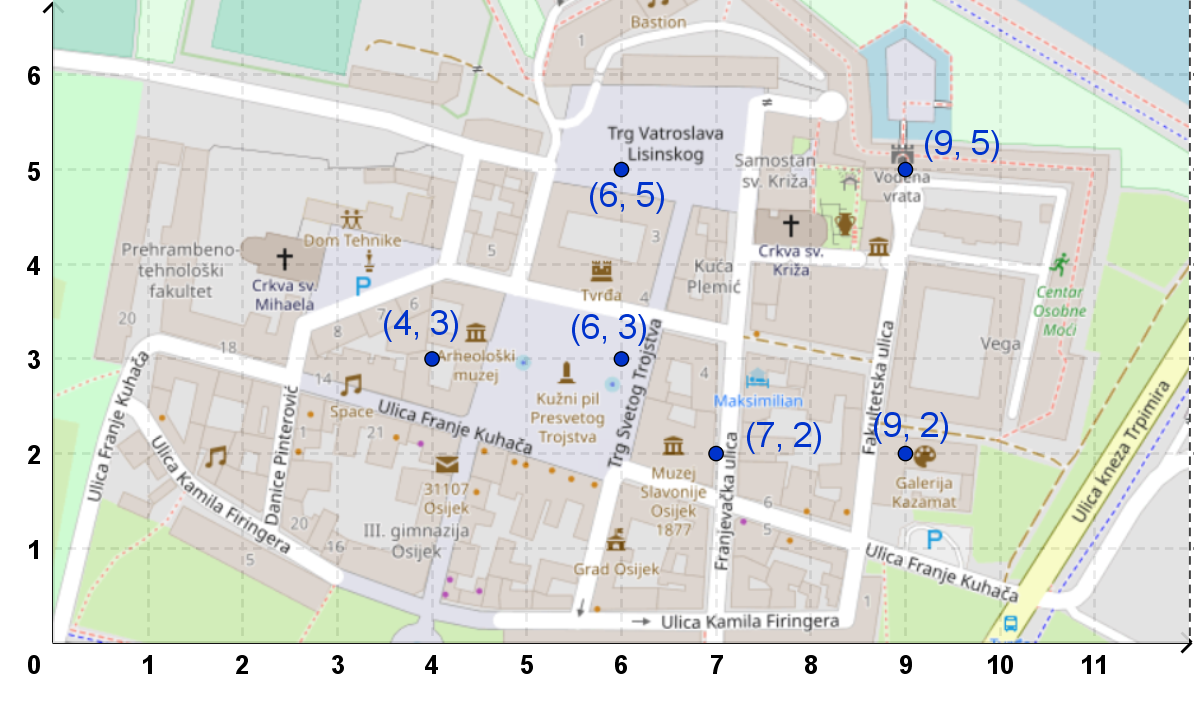
Luna i Noa krenuli su na izlet u najveći slavonski grad. Odlučili su posjetiti znamenitosti njegovog starog dijela koji se zove Tvrđa. Posjetit će muzeje označene uređenim parovima i trgove označene uređenim parovima i galeriju označenu uređenim parom i povijesne znamenitosti označene uređenim parovima i
a. U kojem se gradu nalaze dječak i djevojčica?
b. Imenuj trgove i muzeje koje su odlučili posjetiti.
c. Imenuj povijesne znamenitosti koje su odlučili posjetiti.
d. Imenuj mjesta označena uređenim parovima koji imaju jednake prve članove.
e. Uoči uređene parove pridružene Arheološkom muzeju i Trgu Svetog Trojstva. Što im je jednako, a što različito?
a. Nalaze se u Osijeku.
b. Odlučili su posjetiti Trg Svetog Trojstva i Trg Vatroslava Lisinskog, kao i Arheološki muzej i Muzej Slavonije.
c. Odlučili su posjetiti Bastion i Vodena vrata.
d. Jednake prve članove imaju Muzej Slavonije i Bastion, Galerija Kazamat i Vodena vrata, Trg svetog Trojstva i Trg Vatroslava Lisinskog.
e. Spomenuta mjesta imaju jednake druge članove, dok im prvi članovi nisu jednaki.