Učitavanje
Svg Vector Icons : http://www.onlinewebfonts.com/icon
DOS 8 Interdisciplinarne teme
/
Na granici (ne)mogućeg

30. Smisao života jednog korijena

Popis segmenata i interakcija u videolekciji. Nakon otvaranja pojedine interakcije ili anotacije, pomoću gumba Zatvori prikaz nastavite videolekciju.

Svg Vector Icons : http://www.onlinewebfonts.com/icon

Što ću naučiti

  • HJ 2 Naučit ćete uočiti strukturne dijelove problemskog članka.
  • MAT 1 Naučit ćete odrediti točnu i približnu vrijednost drugog korijena racionalnog broja.
  • MAT 2 Naučit ćete izračunati duljinu stranice kvadrata zadane površine.
  • MAT 3 Naučit ćete što je i kako se konstruira Pitagorino stablo i spirala drugog korijena.
  • HJ 1 Naučit ćete koja su obilježja problemskog članka.
  • HJ 3 Naučit ćete koji su postupci pri pisanju problemskog članka.
  • HJ 4 Naučit ćete pisati problemski članak.
Svg Vector Icons : http://www.onlinewebfonts.com/icon

Podijeli ovu lekciju

Za one koji žele znati više

Iako korjenovanje kao računsku radnju poznajemo još iz doba starih Babilonaca i Egipćana, tek je u 16. stoljeću njemački matematičar Christoff Rudolff prvi uveo zapis korijena, ali bez crtice iznad broja uz uporabu zagrada.
Ovako su se tad zapisivale te jednakosti: √(16) = 4, √(49) = 7, √(225) = 15.

Kako bi izbjegao pisanje zagrada, crticu je na korijen u 17. stoljeću prvi stavio Rene Descartes te se ona zadržala do danas.

#1 Zadatak

U sljedećem zadatku izračunajte i upišite točne vrijednosti drugih korijena zadanih brojeva u odgovarajuću ćeliju. 

81
121
196
256
#2 Zadatak

U sljedećem zadatku označite točan odgovor.

Što od navedenoga vrijedi za x = 160 ?

#3 Zadatak

Sljedeći zadatak riješite s pomoću grafičkog prikaza.

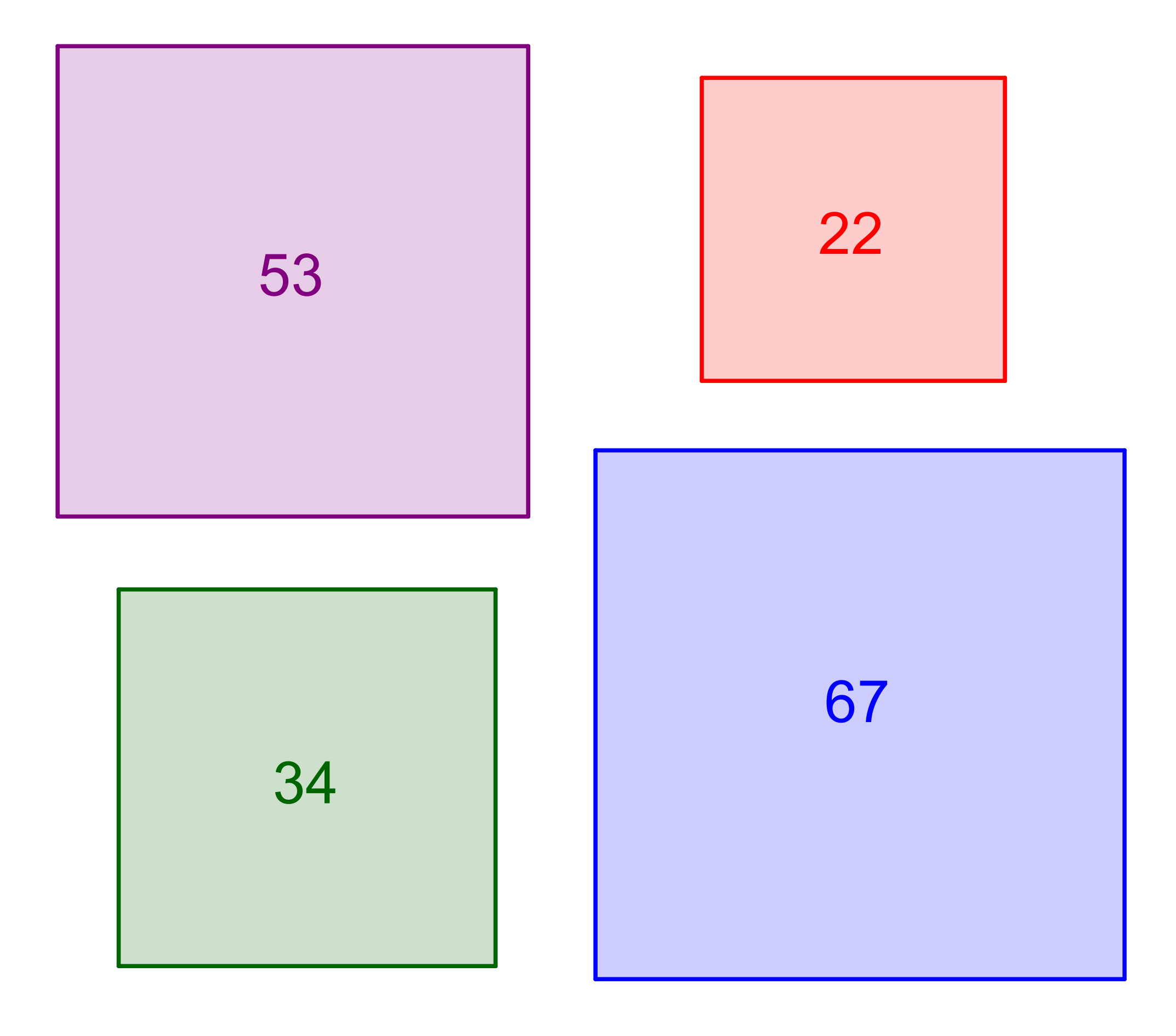
Na slici su prikazana četiri kvadrata. U svakom je kvadratu zapisana njegova površina (u cm2 ). Ispod grafičkog prikaza nalaze se moguće vrijednosti duljina stranica tih kvadrata (u cm). 
Procijenite koja od navedenih vrijednosti duljina stranica odgovara kojem kvadratu pa je smjestite uz njega. 

Oznake smjestite desno pored broja.

Slika
8.2
4.7
5.8
7.3

Za one koji žele znati više

Geometrijski fraktali

Geometrijski su fraktali samoslični geometrijski oblici. Koji god dio fraktala promatrali pod povećalom i koliko god ga puta uvećali, on će uvijek biti identičan cijelom fraktalu. Najpoznatiji su primjeri geometrijskih fraktala Kochova krivulja, trokut Sierpińskog, Cantorov skup i Pitagorino stablo.

Procjena znanja

U sljedećem zadatku označite točan odgovor.

Kolika je približna vrijednost drugog korijena  70 ? Pokušajte odrediti točan odgovor procjenom vrijednosti (bez uporabe džepnog računala).

U sljedećem zadatku razvrstajte prirodne brojeve prema uputi. Označite broj i smjestite ga u odgovarajući stupac.

Razvrstajte brojeve na potpune kvadrate i one koji nisu potpuni kvadrati prirodnih brojeva.

36
91
144
64
8
136
50
9
POTPUNI KVADRATI
NISU POTPUNI KVADRATI

U sljedećem zadatku odgovorite na pitanja odabirom pojmova u padajućem izborniku.

Pitagorin poučak govori o vezi među stranicama

  trokuta. 

površina kvadrata nad katetama jednak je površini kvadrata nad hipotenuzom.

Sljedeći zadatak riješite uparivanjem odgovarajućih pojmova iz desnog i lijevog stupca. To učinite tako da kliknete na pojam koji želite pomaknuti, a zatim kliknite na polje u koje ga želite smjestiti.

Spojite pojam i njegovo svojstvo.

Pitagorino stablo Geometrijski oblik sastavljen od pravokutnih trokuta jedne katete duljine 1.
Pitagorin poučak Samosličan geometrijski oblik koji nastaje višestrukim grafičkim prikazom Pitagorina poučka.
Spirala drugog korijena Broj koji kvadriran daje x.
Drugi korijen broja x Zbroj površina kvadrata nad katetama jednak je površini kvadrata nad hipotenuzom.

Sljedeći zadatak riješite uparivanjem odgovarajućih pojmova iz desnog i lijevog stupca. To učinite tako da kliknete na pojam koji želite pomaknuti, a zatim kliknite na polje u koje ga želite smjestiti.

Navedene dijelove strukture problemskog članka povežite s njegovim objašnjenjem. 

UVOD autor upozorava na postojanje aktualnog problema
GLAVNI DIO autor nudi moguća rješenja razgovarajući sa sugovornicima i istražujući različite izvore; ispituje uzroke i posljedice neke pojave
ZAKLJUČAK autor prihvaća najbolje među ponuđenim rješenjima

Razvrstajte rečenice s obzirom na to odnose li se na uvod, glavni dio ili zaključak problemskog članka. 

Analiza uzroka problema.
Opis uočenog problema.
Iznošenje posljedica primjene predloženog rješenja. 
Uočavanje problema.
Iznošenje prijedloga za rješenje problema.
Razmatranje posljedica problema.
Izbor najboljeg rješenja.
UVOD
GLAVNI DIO
ZAKLJUČAK 

U sljedećem zadatku poredajte pojmove prema zadanom kriteriju. To učinite tako da kliknete na određeni pojam.

Odredite redoslijed radnji za pisanje uspješnoga problemskog članka.

1. ANALIZA REZULTATA ANKETE
2. PISANJE ČLANKA
3. ISTRAŽIVANJE PROBLEMA
4. UOČAVANJE PROBLEMA
5. PROVOĐENJE ANKETE

U sljedećem zadatku dopunite rečenice ponuđenim riječima i izrazima tako da tekst o problemskom članku bude točan. To učinite tako da pojmove smjestite na točno mjesto u rečenici. 

Problemski je članak čija je tema kakav aktualan U takvu se tekstu istražuju razni oblici njegovi te predlažu Problemski članak ima strukturu. U članka ističe se i objašnjava problem kojim se tekst bavi. U istražuju se uzroci, posljedice i  problema, a u se izabire najbolje rješenje.  članka ne može, i ne treba, znati sve o problemu o kojem piše, ali treba razgovarajući s nekim ili istražujući različite .

glavnom dijelu
zaključku
uvodu
tekst
tražiti odgovore
rješenja.
moguća rješenja
trodijelnu
Autor
problem ili društvena pojava.
problema,
uzroci i posljedice
izvore

Sljedeći zadatak riješite s pomoću priloženih fotografija. Označite polje uz fotografiju koja prikazuje točan odgovor.

Koja fotografija odgovora naslovu problemskog članka Kako poboljšati mentalno zdravlje djece i mladih?

Slika a
Slika a
Slika b
Slika b
Slika c
Slika c
Slika d
Slika d

Sljedeći zadatak riješite s pomoću priloženih fotografija. Označite polje uz fotografiju koja prikazuje točan odgovor.

Koja fotografija odgovora naslovu problemskog članka Nezdrava prehrana utječe na zdravlje građana?

Slika a
Slika a
Slika b
Slika b
slika c
slika c
slika d
slika d

Problemski članak mora biti vjerodostojan.  

Problemski članak mora imati više od 300 riječi. 

Problem o kojem ćete pisati, može se otkriti provođenjem ankete. 

Autor problemskog članka ne mora znati sve o temi o kojoj piše, ali je mora dobro istražiti.

Autor ne treba istražiti različite izvore podataka.

Problemski članak mora biti jezično točan.

30. Smisao života jednog korijena

Popis segmenata i interakcija u videolekciji. Nakon otvaranja pojedine interakcije ili anotacije, pomoću gumba Zatvori prikaz nastavite videolekciju.

Svg Vector Icons : http://www.onlinewebfonts.com/icon

Što ću naučiti

  • HJ 2 Naučit ćete uočiti strukturne dijelove problemskog članka.
  • MAT 1 Naučit ćete odrediti točnu i približnu vrijednost drugog korijena racionalnog broja.
  • MAT 2 Naučit ćete izračunati duljinu stranice kvadrata zadane površine.
  • MAT 3 Naučit ćete što je i kako se konstruira Pitagorino stablo i spirala drugog korijena.
  • HJ 1 Naučit ćete koja su obilježja problemskog članka.
  • HJ 3 Naučit ćete koji su postupci pri pisanju problemskog članka.
  • HJ 4 Naučit ćete pisati problemski članak.
Svg Vector Icons : http://www.onlinewebfonts.com/icon

Podijeli ovu lekciju

Pojmovnik

Povezane lekcije

Popis povezanih videolekcija za čitače ekrana

  1. Tema 5: Na granici (ne)mogućeg - Ishodi učenja: MAT OŠ D.8.2. Primjenjuje oplošje i volumen geometrijskih tijela., MAT OŠ D.8.4. Odabire i preračunava odgovarajuće mjerne jedinice., MAT OŠ A.8.2. Računa s potencijama racionalne baze i nenegativnoga cjelobrojnog eksponenta., FIZ OŠ C.8.7. FIZ OŠ D.8.7. Povezuje pojavu titranja i prijenos energije valom., FIZ OŠ D.8.2. Analizira učinke električne struje i magnetizam., FIZ OŠ D.8.3. Analizira električnu struju i napon te primjenjuje koncepte rada i snage., MAT OŠ A.8.1. Računa s korijenima., MAT OŠ D.8.1. Primjenjuje Pitagorin poučak, OŠ HJ A.8.4. Učenik piše raspravljačke tekstove u skladu s temom i prema planu.", "FIZ OŠ C.8.7. FIZ OŠ D.8.7. Povezuje pojavu titranja i prijenos energije valom., OŠ HJ A.8.4. Učenik piše raspravljačke tekstove u skladu s temom i prema planu., OŠ LK C.8.1. Učenik likovnim i vizualnim izražavanjem analizira utjecaj vizualnih komunikacija i prostornoga oblikovanja okoline na vlastiti život te daje prijedlog njezina mogućeg (pre)oblikovanja., OŠ LK C.8.2. Učenik raspravlja o društvenome kontekstu umjetničkoga djela.
    1. Videolekcija 5.1: SF čokolada - Ishodi učenja: MAT 1 Naučit ćete primjenjivati volumen geometrijskih tijela., MAT 2 Naučit ćete odabirati i preračunavati odgovarajuće mjerne jedinice., MAT 3 Naučit ćete računati s potencijama racionalne baze i nenegativnoga cjelobrojnog eksponenta., FIZ 1 Naučit ćete da je svjetlost elektromagnetski val., FIZ 2 Naučit ćete što je valna duljina., FIZ 3 Naučit ćete vezu valne duljine, frekvencije i brzine svjetlosti., FIZ 4 Naučit ćete koji su učinci struje u jednostavnome strujnom krugu., FIZ 5 Naučit ćete analizirati rad i snagu električne struje., HJ 1 Naučit ćete prepoznati obilježja znanstvene fantastike., HJ 2 Naučit ćete imenovati najvažnije autore znanstvenofantastične književnosti.
    2. Videolekcija 5.3: Uhvati val! - Ishodi učenja: FIZ 1 Naučit ćete objasniti što su brijeg i dol vala te prepoznati te dijelove vala na primjerima., FIZ 2 Naučit ćete razlikovati valne fronte i valne zrake., FIZ 3 Naučit ćete opisati fizikalna svojstva vala (period, frekvenciju, amplitudu i valnu duljinu)., FIZ 4 Naučit ćete kako se energija prenosi titranjem čestica sredstva., FIZ 5 Naučit ćete koncept odbijanja valova i zakon odbijanja valova., FIZ 6 Naučit ćete povezati frekvenciju, valnu duljinu i brzine vala., HJ 1 Naučit ćete svrhu i važnost životopisa: zašto je životopis ključan dokument u profesionalnom razvoju i kako može utjecati na izglede za zaposlenje., HJ 2 Naučit ćete prepoznati strukturu životopisa: razumjeti ključne dijelove životopisa i kako ih iskoristiti za prikazivanje profesionalnoga iskustva, vještina i postignuća., GK 1 Naučit ćete opisati obilježja instrumentalnih dijelova opere., GK 2 Naučit ćete prepoznati obilježja uvertire i intermezza., GK 3 Naučit ćete slušno razlikovati reprezentativne primjere opernih brojeva uvertire i intermezza.
    3. Videolekcija 5.4: Zelene metropole - Ishodi učenja: Naučit ćete objasniti uzročno-posljedičnu vezu izgaranja fosilnih goriva i onečišćenja zraka., Naučit ćete opisati utjecaj povećane koncentracije ugljikova dioksida na okoliš i živa bića., Naučit ćete povezati utjecaj površina s pojavom toplinskih gradskih „otoka“., Naučit ćete navesti kriterije ostvarivanja statusa zelene metropole., Naučit ćete objasniti kako funkcioniraju zelene metropole., Naučit ćete koja je uloga arhitekata, krajobraznih arhitekata i urbanista u stvaranju zelenih metropola., Naučit ćete koja je uloga zelenih površina u urbanom kontekstu., Naučit ćete koje vrste parkova postoje.
    4. Videolekcija 5.5: Po uzoru na prirodu - Ishodi učenja: BIO 1 Naučit ćete prepoznati probleme s kojima se čovjek suočavao u svojim izumima., MAT 1 Naučit ćete što su preslikavanja u ravnini, koje su osnovne vrste preslikavanja u matematici te kako se konstruiraju slike likova., LIK 1 Naučit ćete prepoznati land art kao umjetnički smjer., LIK 2 Naučit ćete primjenjivati land art kao medij izražavanja., LIK 3 Naučit ćete uočiti i prepoznati land art na likovnim primjerima., BIO 2 Naučit ćete povezati prilagodbe organizama s inovativnim rješenjima u arhitekturi i inženjerstvu te prepoznati važnost inovacija.
    5. Videolekcija 5.6: Vjerovali ili ne - Ishodi učenja: BIO 1 Naučit ćete opisati obilježja gena i spolnog razmnožavanja., BIO 2 Naučit ćete razlikovati dominantna i recesivna svojstva te nasljedna i stečena svojstva., BIO 3 Naučit ćete primijeniti postupak križanja u nasljeđivanju svojstava., BIO 4 Naučit ćete opisati određivanje krvnih grupa te njihovo nasljeđivanje., MAT 1 Naučit ćete opisati siguran i nemoguć događaj., MAT 2 Naučit ćete odrediti skup svih povoljnih i skup svih mogućih događaja., MAT 3 Naučit ćete izračunati vjerojatnost slučajnog događaja.

Ovo djelo je dano na korištenje pod licencom Creative Commons Imenovanje-Nekomercijalno-Dijeli pod istim uvjetima 4.0 Hrvatska.

Ovo djelo je dano na korištenje pod licencom Creative Commons Imenovanje-Nekomercijalno-Dijeli pod istim uvjetima 4.0 Hrvatska.