

Kad razmišljate o sutrašnjem vremenu, ishodu nekoga sportskog događaja ili samo čekate autobus, često se nesvjesno koristite vjerojatnosti. Takvu vjerojatnost kojom se koristimo bez računanja ili promatranja matematičkih pokusa nazivamo subjektivna vjerojatnost. Subjektivna vjerojatnost je osobno uvjerenje pojedinca o izgledima da se neki događaj dogodi. Često se temelji na iskustvu, osobnom uvjerenju i analizi određene situacije.
Primjerice, ako dulje pratite utakmice domaćega nogometnog kluba, moći ćete bolje procijeniti koliki su mu izgledi za pobjedu u nekoj utakmici.
Pri izradi vremenske prognoze koriste se složeni matematički modeli koji na temelju podataka prikupljenih tijekom duljeg vremena izračunavaju kolika je vjerojatnost za kišu, oblake, sunčano vrijeme, oluje i slično. Primjerice, ako postoje podatci za
dana s vremenskim uvjetima koji su slični današnjim vremenskim uvjetima i ako je od tih
dana u
njih padala kiša, onda procjenjujemo da je vjerojatnost padanja kiše
Naravno, matematički modeli za vremensku prognozu mnogo su složeniji, a ako vas zanima praćenje vremenskih promjena, pogledajte mrežnu stranicu Meteorologija kao znanost.
Pronađite nekoliko različitih vremenskih prognoza za sljedeći tjedan za kraj u kojem živite. Prikupite sve informacije o temperaturi i padalinama te od dostupnih podataka složite vremensku prognozu. U njoj procijenite kolika je vjerojatnost toplog vremena, kiše, snijega... Tijekom tjedna svaki dan bilježite temperature i padaline te usporedite je li vrijeme u skladu s vremenskom prognozom koju ste napisali. Objasnite što je u skladu, a što nije u skladu s vremenskom prognozom. Objasnite na koji se način prognostičari koriste podatcima o prošlome vremenu kako bi predvidjeli buduće vrijeme.
Dopunite rečenicu. Procijenite.
Pomoć:
Vjerojatnost da će padati kiša dobivate tako da broj kišnih dana podijelite brojem svih promatranih dana. Rješenje upišite u obliku cijelog broja na za to predviđeno mjesto.
Dopunite rečenicu.
Procijenite.
Pomoć:
Vjerojatnost da će danas padati snijeg dobivamo tako da broj godina kada je na današnji dan padao snijeg podijelimo brojem svih promatranih godina
Rješenje zapišite u obliku cijelog broja na za to predviđeno mjesto.
Odaberite točan odgovor.
Znanstvenici kažu kako postoji
vjerojatnosti da će sljedeći komet proći blizu Zemlje. To znači:
Primjer 1.
Kada je na televiziji prikazana vremenska prognoza, prognostičarka je rekla da je vjerojatnost da će sutra padati snijeg Kolika je vjerojatnost da sutra neće padati snijeg?
Snijeg će ili padati ili neće padati, ne postoji treća mogućnost. Takve događaje nazivamo suprotni događaji. Dva suprotna događaja čine cjelinu pa je njihova zajednička vjerojatnost
Ako je vjerojatnost da će padati snijeg onda je vjerojatnost suprotnog događaja, tj. da neće padati snijeg
Događaji i za koje vrijedi da ako se dogodi događaj onda se nije dogodio događaj ili ako se nije dogodio događaj onda se dogodio događaj nazivaju se suprotni događaji. Vjerojatnost događaja koji je suprotan događaju dana je formulom:
Iva kaže kako je vjerojatnost da neće položiti ispit
Pomoć:
Rješenje upišite u obliku cijelog broja na za to predviđeno mjesto.
To bi značilo kako Iva najvjerojatnije položiti ispit.
Pomoć:
Pažljivo pročitajte zadatak. Razmislite je li veća vjerojatnost da će Iva položiti ispit ili da neće.
Vjerojatnost se nalazi u pozadini planiranja sportskih strategija, ali i različitih igara na sreću. Primjerice, ako košarkaš Ivo pogađa trice u slučajeva, a Marko u slučajeva, trener će pri planiranju mjesta u ekipi Ivu staviti na položaj s kojeg može bacati trice.
Ako igrate neku društvenu ili kartašku igru, tijekom igranja u glavi ćete smišljati kombinacije karata i promišljati kakvi su vam izgledi da dobijete određenu kartu ili da stanete na neko posebno polje u igri.
Igre na sreću posebno su osmišljene tako da izgledi za dobitak nikad nisu na strani igrača, uvijek su znatno veći izgledi da izgubite nego da dobijete. I ne zaboravite da klađenje i igre na sreću nisu dopušteni za mlađe od
godina.
Kad igra postaje problem
Prekomjerno igranje javlja se kada aktivnost igranja na sreću dobije niz negativnih posljedica pri čemu je ugrožena sigurnost i dobrobit igrača ili njegove obitelji (prijatelja) te kad se negativni utjecaji prošire na širu zajednicu. Kada igrač nije u mogućnosti kontrolirati nagon za igranjem, a izvođenjem tog čina također šteti sebi ili drugima, govorimo o patološkom igranju.
(Izvor: Hrvatska lutrija)
Primjer 2.
Trgovci često organiziraju nagradne igre. Jedna od popularnijih igara je ona s bočicama soka kada se s unutarnje strane čepa nalaze neki simboli ili kodovi koji donose nagradu. Obično svi tada raspravljaju o taktikama i tehnikama kako prepoznati bočicu s dobitnim čepom.
Pogledajte u animaciji kako se računa vjerojatnost dobitka određenog simbola ispod čepa u takvoj igri na sreću.
Na organiziranoj Večeri matematike u jednoj školi ponuđena je tombola. U vreći se nalaze kartice u bojama. Razne boje nose razne nagrade. Ako izvučete crvenu karticu, nećete dobiti ništa na tomboli. Ako izvučete plavu, dobit ćete bombon. Ako izvučete bijelu, dobit ćete jednu ispriku za usmeno ispitivanje iz Matematike, a ako izvučete zelenu, dobit ćete jednu ispriku za nenapisanu zadaću iz Matematike. Crvenih kartica ima plavih ima bijelih i zelenih Kartica se izvlači bez gledanja i vraća u vreću.
Nazovimo događaje prvim slovom boje kartica, = nije dobitna kartica, = dobije se bombon, = isprika za usmeno ispitivanje iz Matematike i = isprika za nenapisanu zadaću iz Matematike.
Plavih kartica ima
a crvenih
ukupan broj kartica za ta dva događaja je
pa povoljnih događaja imamo
od ukupno
ili
Dobitnih kartica ima
pa je vjerojatnost da je izvučena dobitna kartica
(dobitna kartica)
Janko je kupio paketić sa sličicama životinja. U paketiću ima
sličica, on je dobio po jednu sličicu s medvjedom, lisicom, žabom, orlom, vjevericom i pužem. Uzima jednu sličicu nasumce iz paketića i želi je dati maloj sestri. Odredite vjerojatnost da je na izvučenoj sličici određena skupina životinja.
Dovucite vjerojatnosti na određeni postotak.
Izračunajte vjerojatnosti tih događaja i spojite parove.
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Elementarnih događaja ima U paketiću se nalaze sličice na kojima su životinje s krznom, sličica s pticom, sličice na kojima su životinje s kitnjastim repom, a ribe nema ni na jednoj sličici.
Primjer 3.
U automatu u školskom predvorju nalaze se šestari u raznim bojama. Od ukupnog broja šestara je žutih, je sivih, je plavih, a ostalih šestara crvene je boje. Kada ubacite novčić, dobijete jedan, bilo koji šestar.
- Koliko je posto crvenih šestara u automatu?
- Koliko ima svih šestara u automatu?
- Koliko je žutih šestara?
- Kolika je vjerojatnost da dobijete žuti šestar?
- Što zamjećujete? Moramo li znati točan broj šestara ili je dovoljno znati udjel promatranih šestara u cjelini?
- Možete li bez računanja koliko ima plavih šestara odgovoriti kolika je vjerojatnost da dobijemo plavi šestar?
Svih šestara u automatu je Za ostale boje šestara znamo postotak, pa oduzimamo te postotke od
Crvenih je šestara
Znamo da crvenih šestara ima
i da je to
od ukupnog broja šestara. Izračunamo ukupan broj šestara onako kako smo naučili u cjelini s postotcima.
U automatu je ukupno šestara.
Izračunamo koliko ima žutih šestara, komada.
Označimo s događaj da dobijemo žuti šestar,
Zamijetite da je vjerojatnost udjel u cjelini, a to je i postotak, što znači da za izračun vjerojatnosti ne moramo znati točan broj žutih šestara. Ako znamo udjel žutih šestara u cjelini, to nam je dovoljno.
Vjerojatnost da dobijemo plavi šestar je
Ako znamo udjel nekog događaja u cjelini, znamo i vjerojatnost da se dogodi taj događaj.
U ribnjaku je amura, somova, štuka i ostalo su šarani.
Pomoć:
Izračunajte koliko posto je šarana u ribnjaku i pogledajte prethodni primjer.
U 7. b razredu učenika su dječaci, od kojih četvorica ne uče talijanski jezik. Preostalih učenika su djevojčice i one sve uče talijanski jezik.
Zbor jedne osnovne škole ide na natjecanje zborova. Učiteljica im je pripremila sendviče. Tri su sendviča s tunjevinom, sirom i vrhnjem, sa salamom, sirom i majonezom, sa šunkom i vrhnjem, a sa salamom, sirom i rajčicama. Učenici uzimaju umotane sendviče ne znajući koji je sendvič u paketu.
Iva bi željela dobiti sendvič s tunjevinom. Vjerojatnost da će izabrati takav sendvič iznosi
Pomoć:
Pažljivo pročitajte zadatak. Izračunajte vjerojatnost i povucite ju na predviđeno mjesto.
Dora izrađuje šarenu ogrlicu. Iz vrećice s perlicama ne gledajući uzima sljedeću perlicu. U vrećici je zelenih perlica, crvenih perlica i žutih perlica. Preostalih perlica plave je boje.
Pomoć:
Odgovor upišite u obliku cijelog broja na za to predviđeno mjesto.
Iznosi osiguranja života, zdravlja, stanova i automobila također se određuju na temelju vjerojatnosti. Pri određivanju iznosa za obvezno osiguranje automobila u obzir se uzimaju različiti čimbenici, kao što su dob, jačina motora, mjesto registracije i slično. Raspitajte se kakvi su iznosi tog obveznog osiguranja u mjestu u kojem živite, a možete usporediti i utjecaj različitih čimbenika na cijene tog osiguranja, primjerice na mrežnoj stranici autoodgovornost.
Što mislite zašto su premije osiguranja veće u Zagrebu, a manje u Daruvaru?
Primjer 4.
Braća Ivan i Matija trebaju se dogovoriti tko će ići u trgovinu po kruh. Matija je predložio da igraju igru par-nepar. Ivan je stariji i baš mu se ne ide u trgovinu pa je predložio da igraju sličnu igru. Ivan pobjeđuje, tj. ne ide u trgovinu ako im zbroj prstiju pokaže broj kojemu naziv ne počinje slovom D, a Matija pobjeđuje ako im zbroj prstiju pokaže broj kojemu naziv počinje slovom D. Koji je brat predložio poštenu igru?
Matijina igra je pravednija jer su izgledi za pobjedu s parnim i neparnim brojevima pa obojica imaju jednake izglede za pobjedu.
Ivanova igra nije poštena jer brojeva čiji naziv počinje slovom D ima manje. Ako igraju svaki jednom rukom, zbrojeva ukupno može biti a zbrojeva čiji naziv počinje slovom D je pa su Matijini izgledi za pobjedu Zbrojeva čiji naziv ne počinje slovom D ima pa su izgledi da Ivan ne ide u trgovinu
Nina i Martina igraju jednu igricu. Izvlače kartice s mjesecima neprijestupne godine. Ako izvuku mjesec s parnim brojem dana, Nina je pobijedila. Kolika je vjerojatnost Ninine pobjede?
U godini je mjeseci s neparnim brojem dana i mjeseci s parnim brojem dana.
Vjerojatnost da će Nina pobijediti iznosi
Donesite u školu kockice igre Čovječe ne ljuti se. Prebrojite koliko ste kockica donijeli, koliko kojih boja imate i računajte vjerojatnost izvlačenja određene boje.
Osmislite neku poštenu igru s obzirom na broj i boju kockica koje ste donijeli.
Alen počinje s prodajom nekoliko proizvoda koje je sam osmislio. Kada je stavio cijenu kuna, prodao je proizvoda. Uz cijenu od prodao je proizvoda, a uz cijenu od proizvoda. Želi ispitati vjerojatnost prodaje sljedećeg proizvoda ako na njega stavi cijenu , kako bi odlučio hoće li ostaviti tu cijenu ili neće.
Vjerojatnost prodaje sljedećeg proizvoda po cijeni od iznosi Možda bi ipak trebao razmisliti o smanjenju cijene proizvoda.
Farmaceuti tvrde da je na testiranju lijeka od ispitanika imalo glavobolju kao nuspojavu uzimanja lijeka. Tea ne može odlučiti hoće li uzeti lijek ili neće. Kolika je vjerojanost da će i ona imati glavobolju?
Vjerojatnost da će Tea imati glavobolju kao nuspojavu uzimanja lijeka iznosi
Kako je vjerojatnost dobivanja glavobolje mala, Tea bi mogla odlučiti uzeti lijek.
Operacija sive mrene uspješna je u od slučajeva. Baka Ana treba odlučiti hoće li ići na operaciju ili neće. Kolika je vjerojatnost da će i njezina operacija biti uspješna?
Vjerojatnost da će operacija bake Ane biti uspješna iznosi
Iako još postoji vjerojatnost od neuspjeha operacije, baka Ana mogla bi odučiti u korist operacije.
Primjer 5.
Djevojčice se igraju bacajući dvije kockice. Kolika je vjerojatnost da će na kockicama pasti brojevi čiji je zbroj
Rješenje pogledajte u animaciji.
Bacanje dviju kockica složeniji je događaj koji ima
elementarnih događaja. Pri rješavanju zadataka s bacanjem dviju kockica pomoći će vam ova tablica. U tablici su zapisani svi elementarni događaji za bacanje dviju kockica.
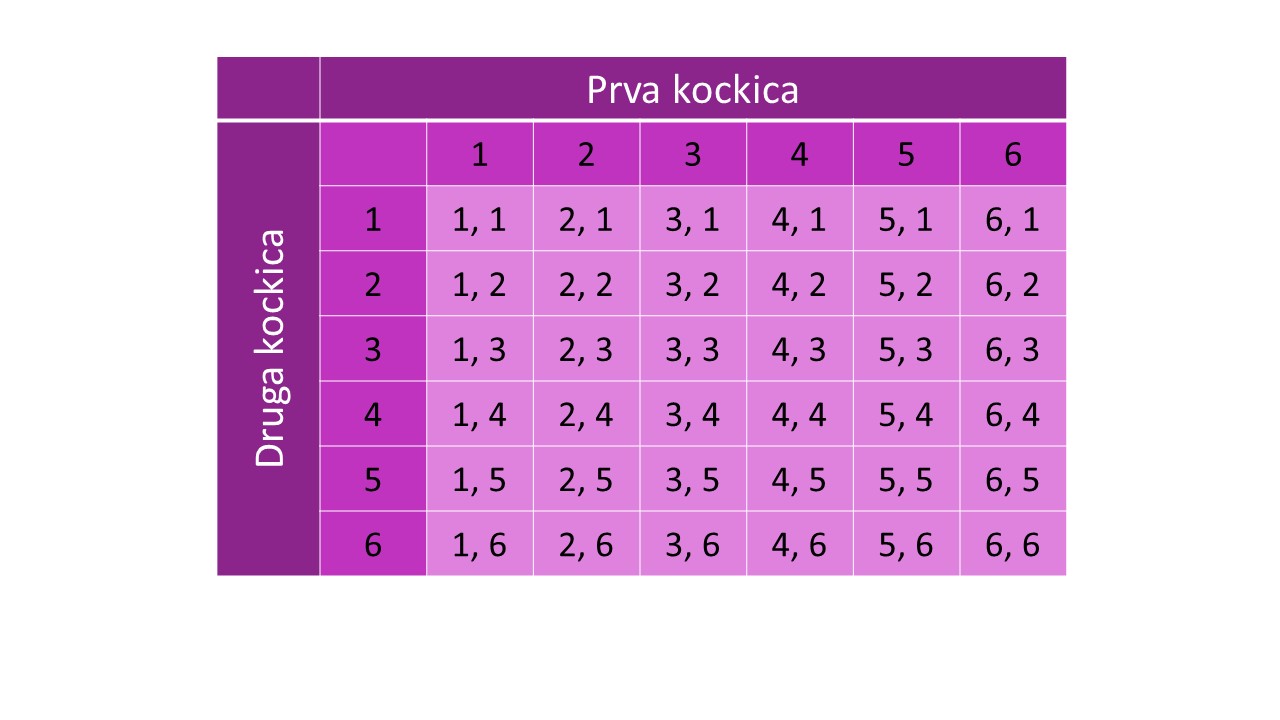
Bacite dvije kockice i odgovorite na pitanje.
Kolika je vjerojatnost da su oba broja koja su pala na kockicama parna?
Pomoć:
Ima takvih parova.
Ivo i Ana bacaju dvije kockice.
Dovucite događaje na određene vrijednosti.
Izračunajte vjerojatnosti tih događaja i spojite parove.
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Za pomoć pogledajte tablicu.
Učenici bacaju dvije kockice. Je li točna izjava jednog učenika?
Pomoć:
Vjerojatnost iznosi
Izvodimo pokus bacanja dviju kockica.
Dovucite događaje na određene vrijednosti.
Izračunajte vjerojatnosti ovih događaja i spojite parove.
|
|
|
|
|
|
|
|
|
|
|
|
Pomoć:
Kod rješavanja zadataka pomozite si tablicom.
O vjerojatnosti govorimo svakodnevno. Svaki dan pratimo vremensku prognozu, govorimo da ćemo vjerojatno nekamo doći, da ćemo vjerojatno dobiti neku ocjenu i izgovaramo još mnogo sličnih rečenica. Vjerojatnost se ne koristi samo u razgovoru i igri, računanje vjerojatnosti u medicini, gospodarstvu, politici, prometu i drugdje vrlo je složen i ozbiljan posao. Ovdje smo samo počeli s računom vjerojatnosti i dotaknuli samo neka područja u kojima se koristi. Provjerite jeste li razumjeli osnove računanja vjerojatnosti kratkom procjenom znanja.
Ako je prognostičarka na televiziji rekla da je velika vjerojatnost da će sljedeći dan biti oborina, a datum je 25. studenoga, što biste mogli taj sljedeći dan odjenuti ili ponijeti sa sobom? Izaberite više odgovora.
Pomoć:
Pozorno pročitajte zadatak.
Sven izvlači nagradni kupon u trgovini. Na kupona nacrtano je voće, na su nacrtani sokovi, na kupona nacrtani su sirevi, a na ostalima su higijenske potrepštine.
Vjerojatnost da će Sven izvući kupon s voćem je najveća.
Pomoć:
Najveća je vjerojatnost da će izvući kupon sa sokovima.
U razredu je
učenika. Kolika je vjerojatnost da je redni broj u imeniku slučajno odabranog učenika paran broj?
Pomoć:
Parnih rednih brojeva u razredu s učenika je
Pomoć:
Zbrojite jabuke i kruške.
Postupak:
Ukupan broj voća u zdjeli je komada, a jabuka i krušaka zajedno je komada.
U šeširu su kartice u raznim bojama s brojevima od do Među karticama su svijetloplave, je ljubičastih, a su narančaste. Boje i brojevi na karticama nemaju međusobno nikakve veze. Luka i Lovro izvlače jednu karticu i vraćaju je natrag u šešir. Luka predlaže igru u kojoj on pobjeđuje ako je na izvučenoj kartici parni broj, a Lovro pobjeđuje ako izvuče karticu s neparnim brojem.
Lovro predlaže igru u kojoj on pobjeđuje ako je izvučena kartica ljubičasta, a Luka pobjeđuje ako je izvučena kartica svijetloplava ili narančasta.
Koji je dječak smislio poštenu igru?
Pomoć:
U Lukinoj igri obojica imaju jednake izglede za pobjedu.
U Lovrinoj igri izgledi da se izvuče ljubičasta kartica veći su od izgleda da se izvuče svijetloplava ili narančasta kartica.
Postupak:
U Lovrinoj igri izgledi da se izvuče ljubičasta kartica su i veći su od izglea da se izvuče svijetloplava ili narančasta kartica. Izgledi da se izvuče svijetloplava ili narančasta kartica iznose