Matematika 2 - Procjena znanja

Prizma je geometrijsko tijelo omeđeno s

međusobno

n

-terokutra te s

n

. Piramida je geometrijsko tijelo omeđeno s

n

-terokutom i

n

.
Krnja piramida je geometrijsko tijelo omeđeno s dva

n

-terokuta i

n

paralelograma

sukladna

slična

dva

trokuta

trapeza

jednim

null

Nazive za dijelove piramide povucite na pravo mjesto.

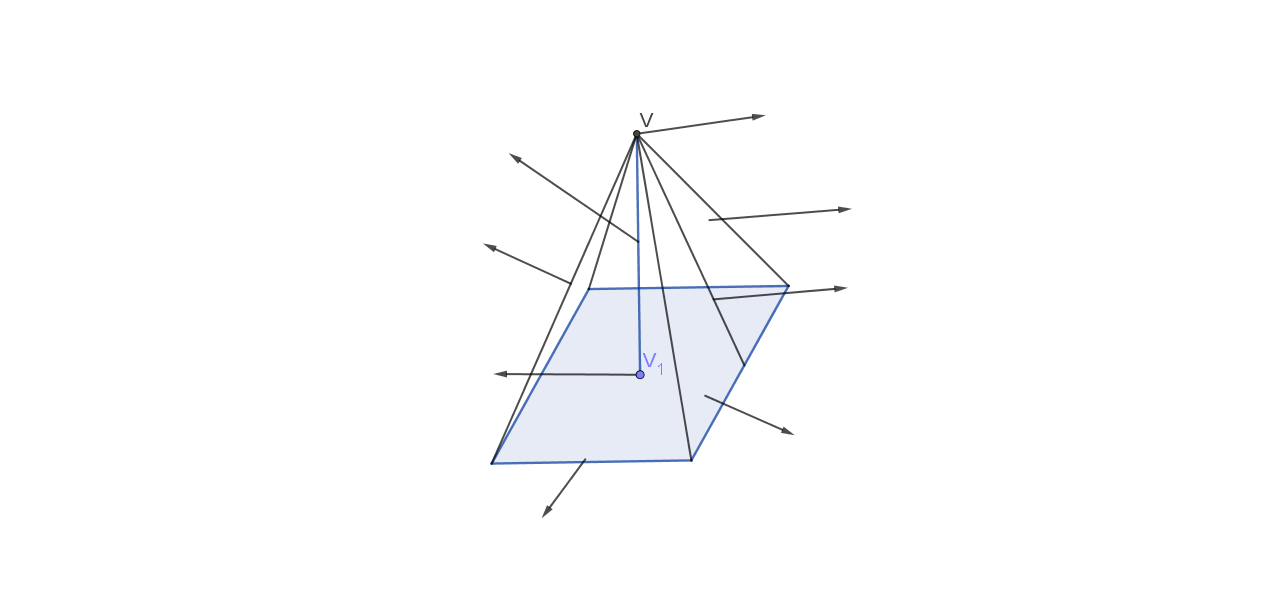
vrh

pobočka

visina pobočke

baza

pobočni brid

visina

nožište visine

osnovni brid

null

Povežite formule s njihovom namjenom.

Obujam prizme	$O = B + P$
Oplošje krnje piramide	$V = \frac{h}{3} (B_{v} + B_{m} + \sqrt{B_{v} B_{m}})$
Oplošje prizme	$V = B \cdot h$
Oplošje piramide	$O = B_{v} + B_{m} + P$
Obujam piramide	$O = 2 B + P$
Obujam krnje piramide	$V = \frac{1}{3} B \cdot h$

null

Označimo li s $V$ broj vrhova poliedra, $S$ broj strana i s $B$ broj bridova, tada vrijedi:

V + S = B - 2

V + B = S + 2

V = B + S + 2

V = B - S + 2

null

Prizma sa šest vrha i devet bridova ima strana. Takva prizma se naziva .

null

Baza prizme je mnogokut.

null

Da bi dva poliedra iste visine imala jednake volumene neophodno je da imaju sukladne baze.

Dovoljno je da imaju jednake površine baza.

null

Obujam piramide ovisi o površini baze i visini piramide.

null

Obujam od $1$ litre jednak je volumenu od:

1 m^{3}

1 {dm}^{3}

1 {cm}^{3}

1 000 {cm}^{3}

null

Odredite obujam prizme čija je baza kvadrat s osnovnim bridom dvostruko većim osnovnog brida pravilne četverostrane prizme obujma $100 {cm}^{3} .$

200 {cm}^{3}

400 {cm}^{3}

800 {cm}^{3}

1 600 {cm}^{3}

null

Akvarij ima oblik kvadra duljina bridova $50$ centimetara, $30$ centimetara i $40$ centimetra. Odredite koliki litara vode je potrebno da bi akvarij napunili do $\frac{3}{4}$ visine.

60

litara

60 000

litara

45

litara

Nije jednoznačno određeno.

null

Površine strana kvadra su $12,$ $15$ i $20$ centimetara kvadratnih. Koliki je obujam kvadra?

60 {cm}^{3}

3 600 {cm}^{2}

100 {cm}^{3}

94 {cm}^{3}

null

Baza kose prizme je jednakostranični trokut sa stranicama duljine $8$ centimetara. Volumen te prizme iznosi $160 \sqrt{3} {cm}^{3} .$ Odredite duljinu bočnog brida u centimetrima ako s ravninom baze zatvara kut od $45 ° .$

5

20 \sqrt{3}

10 \sqrt{2}

20

null

Kut pobočke i ravnine baze pravilne šesterostrane piramide duljine osnovice $10$ centimetara i visine $20$ centimetra iznosi:

24 ° 5' 41 "

26 ° 33' 54 "

58 ° 54' 33''

63 ° 26' 6''

null

Baza piramide je trokut sa stranicama duljine

13,

20

21

centimetar. Pobočke zatvaraju s ravninom baze kutove od

30 ° .

Koliki je volumen te piramide u centimetrima kubnim?

null

Krnja piramida obujma

74 {dm}^{3}

ima površine baza

16 {dm}^{2}

9 {dm}^{3} .

Odredite duljinu visine krnje piramide u centimetrima.

null

Procjena znanja

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: