

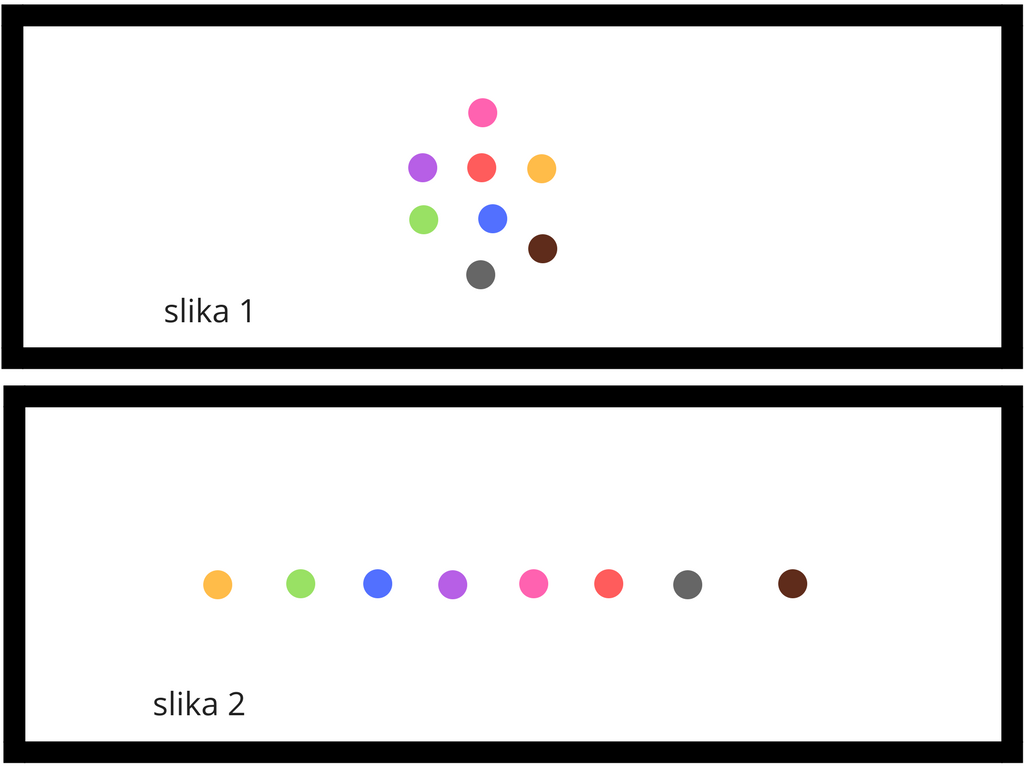
Po čemu se razlikuju slika 1 i slika 2?
Na slici 1 točke ne leže na istom pravcu, a na slici 2 točke leže na istom pravcu.
Nekolinearne točke su točke koje ne leže na istom pravcu. Kolinearne točke su točke koje leže na istom pravcu.
Dvije točke u ravnini uvijek su kolinearne.
Pomoć:
Nacrtajte bilo koje dvije točke u ravnini i spojite ih pravcem. Možete li to učiniti za svake dvije točke u ravnini?
Tri točke u ravnini uvijek su kolinearne.
Pomoć:
Nacrtajte bilo koje tri točke u ravnini i ravnalom ih pokušajte spojiti u pravac.
Možete li ih spojiti ravnalom bez obzira na to kako ste ih nacrtali u ravnini?
Pravac je određen dvjema točkama u ravnini.
Nacrtajte u bilježnicu dvije točke i u ravnini.
e. Zabodite šestar u jednu točku na simetrali dužine i pokušajte opisati kružnicu koja prolazi rubnim točkama dužine
f. Ponovite postupak iz e. podzadatka za još jednu točku simetrale dužine
g. Jeste li mogli ponoviti postupak za svaku točku simetrale?
h. Koliko ima kružnica koje prolaze točkama i
Kružnica koje prolaze kroz točke i u ravnini ima beskonačno mnogo.
Pomoć:
Bilo koja točka na simetrali dužine može biti središte kružnice koja prolazi točkama i u ravnini.
i. Gdje se nalaze središta svih tih kružnica?
Što primjećujete?
Simetrala svake tetive kružnice prolazi središtem kružnice.
Donesite u školu razne predmete kružnog oblika. Organizirajte se u skupine. Na papir ocrtajte rub oko donesenog predmeta. Odmaknite predmet i pokušajte odrediti središte dobivene kružnice. Najprije pokušajte otprilike, a zatim konstrukcijom.
Ako ne znate kako bi konstrukcijom odredili središte, prisjetite se da simetrala tetive kružnice prolazi njezinim središtem.
Prisjetite se i da se dva neparalelna pravca sijeku u jednoj točki.
Znači da će se simetrale dviju tetiva sjeći u jednoj točki, a kako obje prolaze središtem kružnice, sjeći će se baš u središtu kružnice.
Dvije tetive dobili smo uz pomoć
točke na kružnici. Možemo li nacrtati dvije tetive kružnice s manje od
točke?
Ponovimo:
Kroz jednu točku u ravnini možemo nacrtati beskonačno mnogo pravaca (slika 1).
Pravac je određen dvjema točkama, što znači da kroz dvije točke u ravnini možemo nacrtati točno jedan pravac (slika 2).
Kroz dvije točke u ravnini možemo nacrtati beskonačno mnogo kružnica (slika 3).
Ako imamo tri nekolinearne točke u ravnini, možemo ih spojiti u najmanje dvije dužine (slika 4).
Svakoj od tih dužina konstruirajmo simetralu (slika 5).
Na simetralama se nalazi središte kružnice koja prolazi rubnim točkama svake dužine.
Simetrale se sijeku u točno jednoj točki
ako su točke nekolinearne, pa je točno jedno središte kružnica zajedničko (slika 6).
Središte
je jednako udaljeno od dviju rubnih točkaka jedne dužine, i od dviju rubnih točaka druge dužine, ali jedna točka je zajednička, pa možemo zaključiti da je središte jednako udaljeno od svih triju rubnih točaka tih dužina.
Ta udaljenost je polumjer kružnice koju možemo nacrtati oko dobivenog središta
i koja prolazi kroz tri zadane nekolinearne točke (slika 7).
S obzirom na to da je točno jedno središte i jedna duljina polumjera, zaključujemo da možemo nacrtati točno jednu kružnicu sa središtem
koja prolazi kroz tri nekolinearne točke u ravnini.
Kružnica je određena trima nekolinearnim točkama u ravnini.
U sljedećoj GeoGebrinoj simulaciji uvjerite se u tvrdnju tako da rasporedite točke bilo gdje po ekranu. Za bilo koji nekolinearni raspored točaka možete klikom na ljubičasti gumb nacrtati kružnicu koja prolazi svim trima točkama. Točke u ravnini možete sami pomicati mišem nakon što kliknete na narančasti gumb "ponovno".

Svake
nekolinearne točke leže na istoj kružnici.
Pomoć:
Nacrtajte četiri nekolinearne točke u ravnini sličnog položaja kao u zadatku. Spojite točke u dužine, nacrtajte simetrale dužina i uočite da se ne sijeku u jednoj točki, što znači da ne možemo nacrtati jednu kružnicu koja prolazi kroz sve točke.
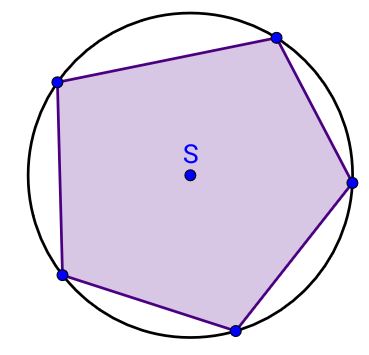
Ako su točke u položaju da se može nacrtati kružnica koja prolazi kroz sve
točke, kažemo da smo četverokutu opisali kružnicu. Takav četverokut zove se tetivni četverokut.
Ako imamo više nekolinearnih točaka u ravnini, možemo ih spojiti u mnogokut.
Ako možemo nacrtati jednu kružnicu koja prolazi kroz sve te točke, kažemo da smo mnogokutu opisali kružnicu.
Nacrtajte u bilježnicu tri nekolinearne točke. Konstruirajte kružnicu koja prolazi kroz te tri točke.
Nacrtajte
u bilježnicu
trokut
u ravnini i opišite mu kružnicu.
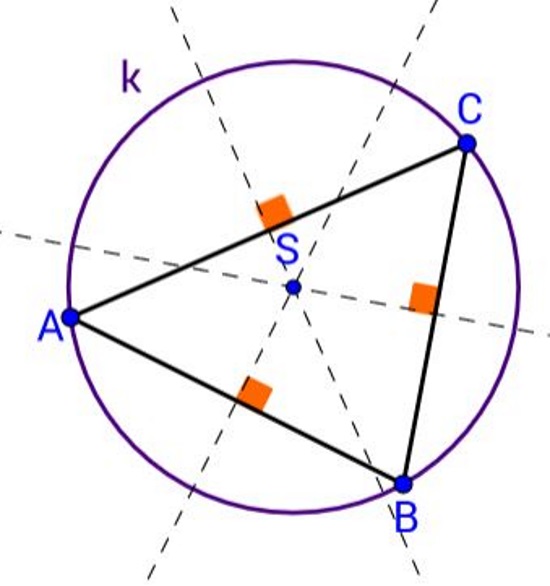
U šestom razredu učili smo da se središte trokutu opisane kružnice nalazi u sjecištu simetrala stranica tog trokuta. Sada ćemo to povezati.
Trokut ima tri vrha, to su tri nekolinaerne točke u ravnini. Kroz tri točke možemo nacrtati točno jednu kružnicu. Ta kružnica je opisana trokutu a stranice trokuta su tetive kružnice.
Mogli smo nacrtati i simetrale samo dviju stranica tog trokuta, ali ovako je slika potpunija i ljepša.
Tri susjedna sela u Slavoniji, koja ne leže uz istu ravnu cestu, žele imati dobru internetsku vezu, pa im treba novi odašiljač. Gdje će postaviti odašiljač da svi mogu imati jednako dobru vezu?
Tri sela su kao tri nekolinearne točke u ravnini. Odašiljač treba biti jednako udaljen od sva tri sela. Ako odašiljač nacrtamo kao jednu točku u sredini, to će biti središte kružnice koja treba prolaziti kroz sva tri sela, tj. kroz tri nekolinearne točke.
Odašiljač je jednako udaljen od sva tri sela i vidi se da će svi imati jednaku internetsku vezu.
Da smo inženjeri, uzeli bismo kartu, na njoj označili ta tri sela i opisali kružnicu na kojoj leže točke koje predstavljaju sela s pomoću simetrala stranica, kako je objašnjeno u prethodnim zadacima, te na mjestu gdje je središte kružnice postavili odašiljač.
Kopirajte dio karte, odaberite tri mjesta na karti i nacrtajte točku koja će biti jednako udaljena od sva tri mjesta. Promislite što bi se moglo sagraditi na tom mjestu a da koristi svim trima mjestima.

Kad postavljamo odašiljače, trebamo imati na umu da se valovi šire kružno i znati kako se ti kružni valovi, ako je više odašiljača u blizini, mogu preklapati.

Pogledajte sliku i razmislite u kojem međusobnom položaju mogu biti kružnice u ravnini.
Kružnice se mogu sjeći.
Kružnice se mogu dodirivati.
Kružnice nemaju zajedničkih točaka.
U ravnini su nacrtane dvije kružnice i takve da je duljina polumjera
veća od duljine polumjera
U animaciji pogledajte u kojim međusobnim položajima mogu biti nacrtane te dvije kružnice i što se događa s udaljenošću njihovih središta.
Kružnice i nacrtane su u ravnini tako da je udaljenost njihovih središta U kojem su međusobnom položaju te dvije kružnice u ravnini?
Pomoć:
Nacrtajte kružnice u bilježnicu i provjerite u kojem su međusobnom položaju u ravnini.
Konstruirajte u bilježnici dvije kružnice promjera
i
koje se dodiruju iznutra u jednoj točki.
U ravnini su nacrtane kružnice
i
Promjer kružnice
je
a promjer kružnice
je
Ako su njihova središta udaljena
u kojem su međusobnom položaju te dvije kružnice u ravnini?
Pomoć:
Izračunajte duljine polumjera kružnica i preračunajte sve u iste mjerne jedinice.
Postupak:
Konstruirajte sve u bilježnicu i odredite međusobni položaj dviju kružnica u ravnini.
Dvije kružnice nalaze se jedna unutar druge. Polumjer veće kružnice je
Ako znamo da je udaljenost njihovih središta
koliki može biti polumjer manje kružnice?
Pomoć:
Ako su dvije kružnice jedna unutar druge, udaljenost njihovih središta manja je od razlike polumjera.
Postupak:
Nacrtajte skicu i riješite nejednadžbu
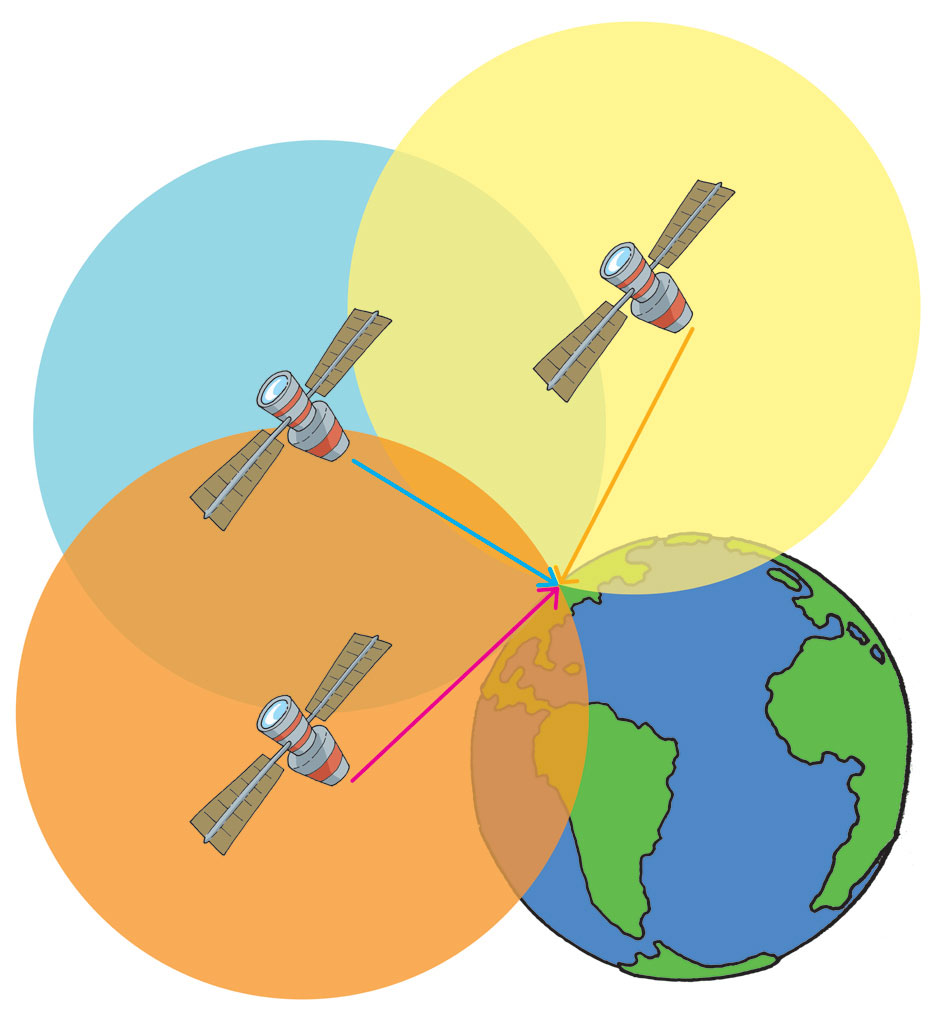
Razne su metode praćenja mobitela. Koliko god neugodno bilo znati da netko prati naš mobitel, praćenje je korisno kad mobitel izgubimo ili primjerice pri traženju nestalih osoba. Jedna od metoda koja ne treba nikakav softver je triangulacija. Triangulacija je postupak utvrđivanja točnog položaja na temelju najmanje triju baznih stanica. Uz pomoć triju baznih stanica dobijemo tri kružna prstena koji se sijeku u zajedničkom području koje predstavlja položaj mobitela s preciznošću od metara.
Proces triangulacije primjenjuje se i u satelitskoj navigaciji (GPS), ali tu nije triangulacija između baznih stanica, nego između najmanje triju satelita.
U ovoj jedinici ponovili smo da je pravac određen dvjema točkama u ravnini, a naučili ste da je kružnica određena trima nekolinearnim točkama u ravnini. To znači da postoji točno jedan pravac koji možemo nacrtati kroz dvije točke u ravnini i točno jedna kružnica koju možemo nacrtati kroz tri točke u ravnini.
Za kraj pogledajte interaktivni zadatak Baze na Antarktici, autora Damira Belavića, u kojem trebate odrediti gdje će biti skladište hrane za tri znanstvene baze na Antarktici.