

Na početku, prisjetimo se primjera koji smo spominjali učeći proporcionalne veličine, a koji prikazuje ovisnost ukupne cijene o količini, uz zadanu jediničnu cijenu proizvoda. Proučite danu interakciju, a potom odgovorite na nekoliko pitanja.
Pridružite odgovarajuće pojmove:
|
cijena i količina
|
proporcionalne veličine |
|
graf proporcionalnosti
|
linearna funkcija |
|
funkcija proporcionalnosti
|
polupravac iz ishodišta |
Funkcija proporcionalnosti linearna je funkcija kojoj je vrijednost koeficijenta
Formule funkcija rasporedite na odgovarajuća mjesta. Redoslijed slaganja formula u određeni skup neka ovisi o veličini koeficijenta i to od najmanjega prema najvećemu.
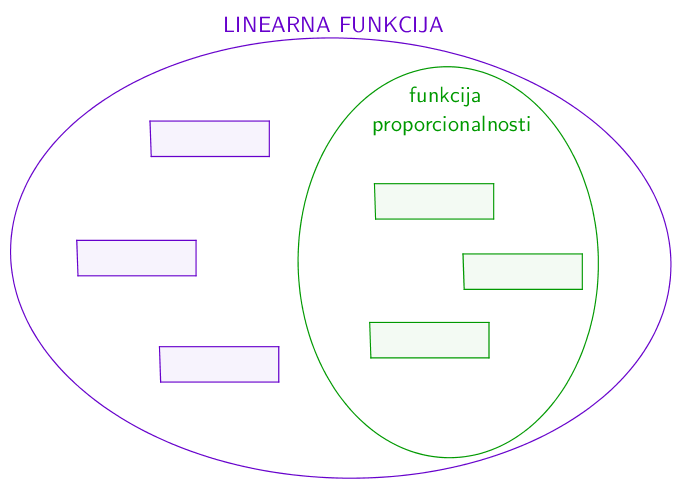
Pomoć:
Nakon što odredite koje su funkcije funkcije proporcionalnosti, posložite formule od gore prema dolje uspoređujući veličine koeficijenta
U sljedećem je primjeru zadana linearna funkcija. Možemo li i nju prikazati u pravokutnom koordinatnom sustavu? Pokušajmo.
Primjer 1.
U interakciji koja slijedi zadana je formula linearne funkcije
Izračunajte vrijednosti funkcije za zadane argumente pa odredite položaj dobivenih točaka u koordinatnom sustavu.
Uputa: Ukoliko ste točno izračunali traženu vrijednost, lijevo od tablice će se pojaviti točka koju je potrebno alatom Pomicanje postaviti na odgovarajući položaj u koordinatnom sustavu u ravnini.
Alati koje možete koristiti su, redom: Pomicanje, Pravac, Izbriši.
Točke koje ste ucrtali u koordinatni sustav pripadaju jednom pravcu. Nacrtajte ga koristeći se alatom za crtanje pravca.
Primjer 2.
Nacrtajte skup svih točaka u pravokutnom koordinatnom sustavu ako za njihove koordinate vrijedi
Uputa: Ako ste točno izračunali traženu vrijednost, pored tablice pojavit će se točka koju je potrebno alatom Pomicanje postaviti na odgovarajući položaj u koordinatnom sustavu u ravnini.
Umjesto zadanih vrijednosti za mogli smo zadati i bilo koje druge racionalne brojeve. Zadajte ponovno nekoliko vrijednosti broja i za svaki od njih izračunajte odgovarajuću vrijednost a zatim točku istaknite u istom koordinatnom sustavu. Što primjećujete?
Može se primijetiti da i nove točke pripadaju istom pravcu kao i točke koje su zadane u primjeru.
S obzirom na to da smo vrijednosti argumenata uzeli proizvoljno, možemo zaključiti da bi bilo koja točka čije koordinate povezuje zadana jednadžba pripadala istom pravcu pa kažemo da smo nacrtali pravac čija je jednadžba
Želimo li u koordinatnom sustavu u ravnini nacrtati pravac koji je zadan jednadžbom, dovoljno je znati koordinate dviju točaka koje mu pripadaju.
Argument
Svaki je pravac određen s .
Pomoć:
Dvjema zadanim točkama može se nacrtati točno jedan pravac.
Ako je koeficijent smjera razlomak, praktično je kao argument zadati broj koji je:
Pomoć:
Praktično je skratiti argument i nazivnik.
Uvježbajte crtati pravce u koordinatnom sustavu u ravnini koristeći se danim predloškom.
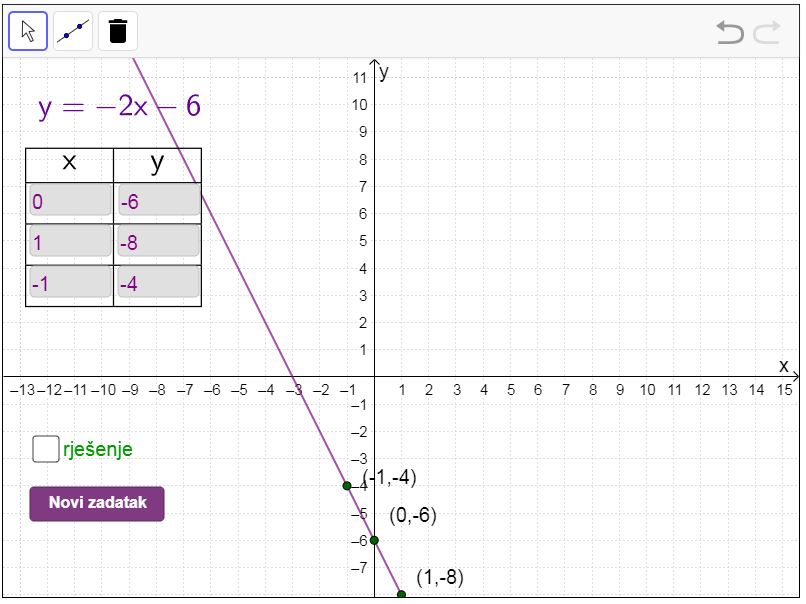
Slijedite dani postupak.
U prethodnim primjerima i zadatcima mogli smo primijetiti da je svaki od pravaca bio zadan jednadžbom oblika Takav oblik jednadžbe pravca naziva se eksplicitna jednadžba pravca.
Eksplicitna jednadžba pravca je jednadžba oblika a određena je racionalnim brojevima i
Dovucite dane jednadžbe u odgovarajuća polja.
Pomoć:
Eksplicitna jednadžba pravca lako se prepoznaje jer u njezinu zapisu s lijeve strane uvijek je samo
Osim eksplicitne jednadžbe pravca, u vašem vas školovanju očekuju i implicitna jednadžba pravca i segmentna jednadžba pravca.
Riječ eksplicitan dolazi iz latinskoga jezika (od explicare), a znači: onaj koji je jasan, onaj koji je jasno iskazan, onaj koji je objašnjen.
Iz eksplicitnog oblika jednadžbe pravca možemo očitati koeficijente
i
a jednako tako možemo zapisati jednadžbu pravca ako su koeficijenti zadani. Provjerimo.
Odredite koeficijente eksplicitne jednadžbe pravca
Pomoć:
Koeficijent je broj uz U zapisu jednadžbe možemo čitati kao
Zadana je eksplicitna jednadžba pravca čiji su koeficijenti
i
Umetnite zadane brojeve na odgovarajuće mjesto.
Primjer 3.
Proučite kako koeficijenti utječu na položaj pravca u koordinatnom sustavu. Pomičite klizače i promatrajte nastale promjene. Pratite istodobno vrijednosti postavljenih klizača i eksplicitnu jednadžbu pravca.
Radi jednostavnosti, koeficijenti su u ovom primjeru cijeli brojevi.
Riješite kviz kako biste provjerili svoje zaključke.
Ako je koeficijent tada je pravac:
Pomoć:
Vratite se na prethodni aplet, postavite klizač na položaj
O koeficijentu nagib pravca.
Pomoć:
Mijenjajte klizač i promatrajte nagib pravca u odnosu na apscisu. Mijenja li se?
Vrijednost koeficijenta možemo izračunati pomoću duljina kateta istaknutog trokuta. Na koji način?
Pomoć:
Na apletu odaberite pomoć kako biste vidjeli istaknuti pravokutni trokut.
Ovisi li nagib pravca o koeficijentu
Pomoć:
Postavite klizač
na neku vrijednost, a mijenjajte položaj klizača
Mijenja li se nagib pravca?
Koeficijent ima vrijednost kao i točke u kojoj pravac siječe .
U eksplicitnoj jednadžbi pravca koeficijent nazivamo koeficijent smjera pravca ili nagib pravca.
U eksplicitnoj jednadžbi pravca koeficijent određuje točku u kojoj pravac siječe os i nazivamo ga odsječak na osi
Rješavajući sljedeću interakciju, provjerit ćete usvojenost značenja koeficijenata eksplicitne jednadžbe pravca. Ponovimo:
koeficijent je nagib pravca, a vrijednost koeficijenta određena je količnikom duljine vertikalne (uspravne) katete i duljine horizontalne (vodoravne) katete pomoćnog pravokutnog trokuta
radi jednostavnosti, odaberite onaj pravokutni trokut kojemu vrhovi šiljastih kutova imaju cjelobrojne koordinate, a katete su usporedne s koordinatnim osima (ili upotrijebite gumb Pomoć)
Odrediti eksplicitnu jednadžbu pravca znači odrediti vrijednosti koeficijenata i i zapisati jednadžbu u obliku
To možemo učiniti ako imamo zadane sljedeće podatke:
koordinate dviju točaka kojima pravac prolazi.
Primjer 4.
Odredimo eksplicitnu jednadžbu pravca kojemu pripada točka i kojemu je koeficijent smjera jednak
Točka pripada pravcu ako njezine koordinate zadovoljavaju jednadžbu pravca. Uvrstimo stoga koordinate točke u jednadžbu pravca
Uvrstimo i i imamo jednadžbu iz koje možemo izračunati vrijednost koeficijenta
Poznata su nam oba koeficijenta pa možemo odrediti eksplicitnu jednadžbu pravca:
Odredite redoslijed radnji koje je potrebno izvršiti kako biste odredili jednadžbu pravca kojemu je zadan nagib i točka kojom prolazi.
Povlačenjem pojma odaberite jednadžbu pravca koji prolazi točkom i ima koeficijent smjera
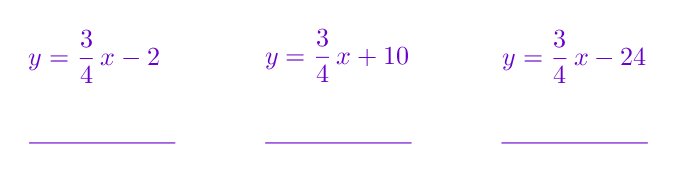
TOČNO!
Odredite eksplicitnu jednadžbu pravca koji sadrži točku i kojemu je koeficijent smjera
Eksplicitna jednadžba zadanog pravca glasi:
Pomoć:
Proučite postupak naveden u prethodnom zadatku.
Primjer 5.
Odredimo eksplicitnu jednadžbu pravca koji sadrži točku i kojemu je odsječak na osi jednak
U jednadžbu pravca uvrstimo zadane veličine pri čemu je i izračunajmo vrijednost nepoznanice
pa tražena jednadžba glasi
Kako glasi eksplicitna jednadžba pravca koji siječe os u točki a sadrži točku
Ako pravac siječe os u zadanoj točki, znači da je odsječak na toj osi jednak upravo ordinati sjecišta, tj. Dalje rješavamo kao u prethodnom primjeru.
Tražena jednadžba pravca je
Primjer 6.
Odredimo eksplicitnu jednadžbu pravca koji prolazi točkama i
Koordinate obiju točaka uvrstit ćemo u eksplicitnu jednadžbu pravca pa ćemo koeficijente izračunati iz dobivenog sustava.
Rješenje sustava je
pa tražena jednadžba glasi
Uz pomoć ponuđene interakcije možete uvježbati određivanje jednadžbe pravca koji prolazi zadanim točkama. Za rješavanje pripremite olovku i papir.
Za one koji žele znati malo više slijede teme Posebni pravci i Implicitna jednadžba pravca.
Je li baš svaki pravac u koordinatnom sustavu graf linearne funkcije? Pogledajmo pravce prikazane na slikama.
Možete se koristiti predloškom za crtanje kako biste istražili ove i slične pravce.
Jesu li i ovo grafovi nekih funkcija?
Ovisi li vrijednost ordinate o vrijednosti apscise?
Imaju li ovi pravci nagib?
Možemo li odrediti odsječak na osi ordinata?
Jednadžba pravca ne mora uvijek biti zapisana u eksplicitnom obliku. Na primjer, ako je zapisana u obliku takvom da je s lijeve strane jednakosti izraz s cjelobrojnim koeficijentima, a s desne strane jednakosti samo nula, govorimo o implicitnom obliku jednadžbe pravca. Takvu jednadžbu jednostavno je prevesti u eksplicitni oblik. Proučimo primjer.
Dana je linearna jednadžba
Zapišimo jednadžbu tako da s lijeve strane bude (s pripadnim koeficijentom), a zatim izrazimo
Želite li se poigrati prevođenjem implicitnog zapisa jednadžbe pravca u eksplicitni, možete to učiniti uz interakciju autorice Željke Dijanić.
Ponovimo i upamtimo:
- koeficijent smjera pravca ili nagib pravca
- odsječak na osi ordinata
- pripada pravcu ako njezine koordinate zadovoljavaju jednadžbu pravca