Kristali metala
- povezati strukturu kristala metala sa svojstvima tvari
- skicirati volumno centriranu, plošno centriranu kubičnu slagalinu
Uvod
Jedinična ćelija je najmanji dio kristala
čijim se ponavljanjem u prostoru može izgraditi cijeli kristal.
Većina metala pripada jednom od tri osnovna tipa jediničnih ćelija.
Jedinična ćelija i kristalna struktura metala
1. Kubična-plošno centrirana jedinična ćelija
(engl. Fcc, face centered cubic)
Od svakog atoma na vrhu kocke jednostavnoj (primitivnoj) jediničnoj ćeliji pripada atoma.
2. Kubična-plošno centrirana jedinična ćelija
(engl. fcc, face centered cubic)
Uvod
Većina metala kristalizira u kubičnom i heksagonskom sustavu. U kubičnom sustavu kristaliziraju, primjerice: , , , , ali i svi alkalijski metali. U heksagonskom sustavu kristaliziraju, primjerice , , i .
Jedinična ćelija i kristalna struktura metala
Jedinična ćelija je najmanji dio kristala čijim se ponavljanjem u prostoru može izgraditi cijeli kristal. Većina metala pripada jednom od tri osnovna tipa jediničnih ćelija.
1. Jednostavna (primitivna) jedinična ćelija
(engl. sc, simple cubic)
Od svakog atoma na vrhu kocke jednostavnoj (primitivnoj) jediničnoj ćeliji pripada atoma.
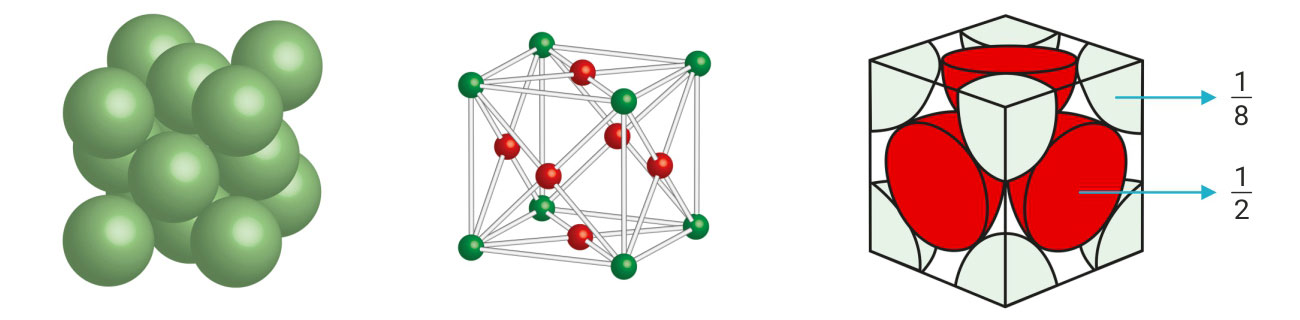
2. Kubična-plošno centrirana jedinična ćelija
(engl. fcc, face centered cubic)
Jedinična je ćelija kocka kojoj se na vrhovima se nalazi 8 atoma.
U sredini svake od 6 ploha nalazi se jedan atom.
Svaki od 8 atoma na vrhovima dijeli osam susjednih jediničnih ćelija.
Samo atoma na vrhu pripada jednoj jediničnoj ćeliji.
Od 8 atoma na vrhovima, jednoj jediničnoj ćeliji pripada 1 atom.
Svaki od 6 atoma na sredini plohe dijeli se sa susjednom jediničnom ćelijom.
Od svakog atoma samo pripada jednoj jediničnoj ćeliji.
Od 6 atoma na plohama, jednoj jediničnoj ćeliji pripadaju 3 atoma.
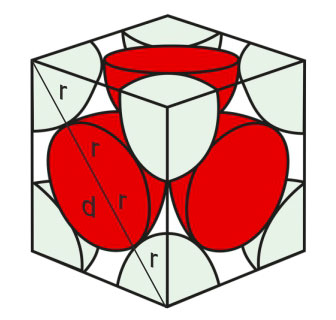
Na slici je prikazan smjer dodirivanja atoma. Atomi se dodiruju na dijagonali plohe.
Jedinična je ćelija kocka na vrhovima koje se nalazi 8 atoma, a u sredini svake od 6 ploha nalazi se jedan atom.
Svaki od 8 atoma na vrhovima dijeli osam susjednih jediničnih ćelija, tako da samo atoma na vrhu pripada jednoj jediničnoj ćeliji. Od 8 atoma na vrhovima, jednoj jediničnoj ćeliji pripada 1 atom.
Svaki od 6 atoma na sredini plohe dijeli se sa susjednom jediničnom ćelijom, pa od svakog atoma samo pripada jednoj jediničnoj ćeliji. Od 6 atoma na plohama, jednoj jediničnoj ćeliji pripadaju 3 atoma.
Na slici je prikazan smjer dodirivanja atoma. Atomi se dodiruju na dijagonali plohe.
Koordinacijski broj je 12 (KB = 12), jer je svaki atom okružen s dvanaest najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja ()
Popunjenost prostora ili koeficijent slaganja () za plošno centriranu kubičnu strukturu iznosi približno 74 %.
2. Kubična-volumno centrirana jedinična ćelija
(engl. Bcc, body centered cubic)
Koordinacijski broj je 12 (KB = 12), jer je svaki atom okružen s dvanaest najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja ()
Popunjenost prostora ili koeficijent slaganja () za plošno centriranu kubičnu strukturu iznosi približno 74 %.
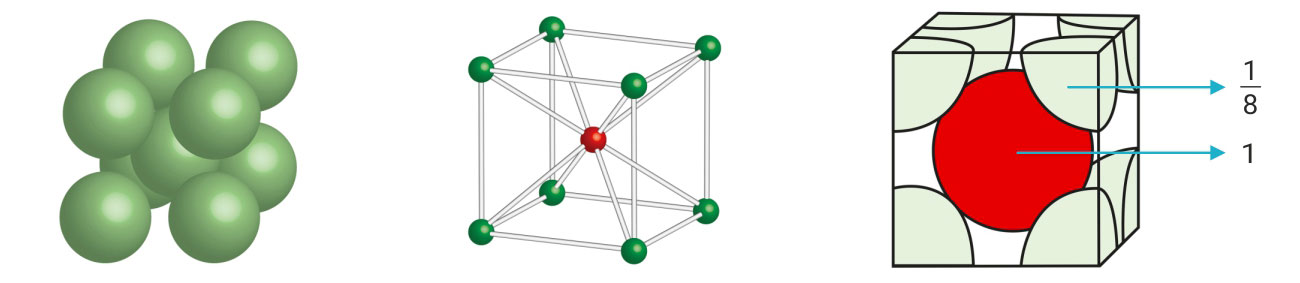
3. Kubična-volumno centrirana jedinična ćelija
(engl. bcc, body centered cubic)
Jediničnoj ćeliji pripada atoma u vrhovima kocke i jedan cijeli atom u središtu kocke.
Smjer dodirivanja atoma je dijagonala kocke, , na kojoj se nalaze 4 radijusa atoma, prema tomu je .
Koordinacijski broj je 8 (KB = 8), jer je svaki atom okružen s osam najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja (Ks)
Popunjenost prostora ili koeficijent slaganja (Ks) za volumno centriranu kubičnu strukturu iznosi približno 68 %.
3. Heksagonska jedinična ćelija
(engl. Hcp, hexagonal close packing)
Jediničnoj ćeliji pripada atoma u vrhovima kocke i jedan cijeli atom u u središtu kocke.
Smjer dodirivanja atoma je dijagonala kocke, , na kojoj se nalaze 4 radijusa atoma, prema tomu je .
Koordinacijski broj je 8 (KB = 8), jer je svaki atom okružen s osam najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja (Ks)
Popunjenost prostora ili koeficijent slaganja (Ks) za volumno centriranu kubičnu strukturu iznosi približno 68 %.
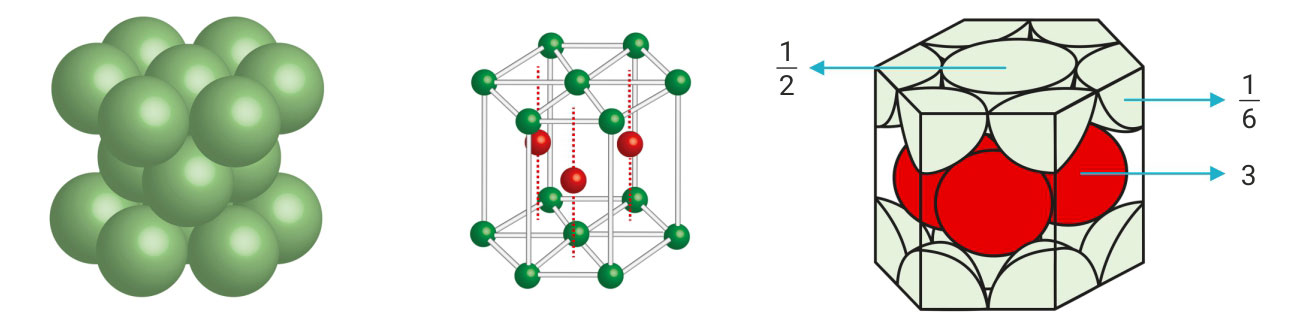
3. Heksagonska jedinična ćelija
(engl. hcp, hexagonal close packing)
Heksagonskoj prizmi pripada atoma u vrhovima prizme, atoma u sjecištu dijagonala baza i 3 atoma u sredini heksagonske prizme.
Ukupno:
Jedinična ćelija heksagonske slagaline je trećina heksagonske prizme.
Broj atoma u jediničnoj ćeliji je 2.
Koordinacijski broj je 12 (KB = 12), jer je svaki atom okružen s dvanaest najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja (Ks)
Popunjenost prostora ili koeficijent slaganja (Ks) za heksagonsku strukturu iznosi približno 74 %.
Heksagonskoj prizmi pripada atoma u vrhovima prizme, atoma u sjecištu dijagonala baza i 3 atoma u sredini heksagonske prizme.
Ukupno:
Jedinična ćelija heksagonske slagaline je trećina heksagonske prizme, prema tome broj atoma u jediničnoj ćeliji je 2.
Koordinacijski broj je 12 (KB = 12), jer je svaki atom okružen s dvanaest najbližih susjednih atoma.
Popunjenost prostora ili koeficijent slaganja (Ks)
Popunjenost prostora ili koeficijent slaganja (Ks) za heksagonsku strukturu iznosi približno 74 %.
Riješeni primjer 1
Krom kristalizira u kubičnom sustavu, a jedinična ćelija mu je prostorno centrirana kocka. Gustoća kroma je 7,19 g cm-3. Izračunajte duljinu brida jedinične ćelije kroma.
Zadano je:
Traži se:
Izradak
Odgovor:
Duljina brida jedinične ćelije kroma je 288 pm.
Na kraju…
Klikom odaberite jedan točan odgovor.
Odaberite točan odgovor.
Koja vrsta kubične slagaline pripada kristalnoj strukturi nekog metala ako jedinična ćelija te kristalne strukture sadržava 4 atoma tog metala?
Unesite odgovore na pripadajuća mjesta.
Želite li pokušati ponovo?