Množina tvari
- objasniti značenje množine tvari i njezine mjerne jedinice, mola
- objasniti prirodu plinova
- objasniti zakon volumnih omjera i Avogadrov zakon
- primijeniti izraz za molarni volumen i njegovu vrijednost u stehiometrijskim izračunima
- povezati množinu, molarnu masu i molarni volumen tvari
Uvod
Koliko molekula vode sadrži jedna kap? Odgovor na postavljeno pitanje saznat ćete pozornim praćenjem videozapisa koji slijedi.
Jedna kap vode sadrži oko 1,00 × 1021 molekula vode.
U kemijskim reakcijama sudjeluje neizmjerno velik broj jedinki.
Zbog toga je dogovoreno da količinu tvari iskazujemo množinom.
Množina tvari
Znak za množinu tvari je n.
Jedinica kojom iskazujemo množinu tvari je mol (znak: mol).
Mol je jedna od sedam osnovnih jedinica Međunarodnog (SI) sustava.
Mol je množina uzorka koji sadrži onoliko jedinki
koliko ima atoma u 0,012 kg najzastupljenijeg izotopa ugljika, .
Taj broj je poznat kao Avogadrov broj i iznosi .
Uz pretpostavku da jedna kap vode sadrži oko 1,00 × 1021 molekula vode, može se zaključiti da u kemijskim reakcijama sudjeluje neizmjerno velik broj jedinki. Zbog toga je dogovoreno da količinu tvari iskazujemo množinom.
Množina tvari
Znak za množinu tvari je n, a jedinica kojom iskazujemo množinu tvari je mol (znak: mol).
Mol je jedna od sedam osnovnih jedinica Međunarodnoga (SI) sustava.
Mol je množina uzorka koji sadrži onoliko jedinki koliko ima atoma u 0,012 kg najzastupljenijeg izotopa ugljika, .
Taj je broj poznat kao Avogadrov broj i iznosi .
ili bilo kojih drugih jedinki sadrži Avogadrov broj tih jedinki.
Brojnost i množina tvari proporcionalne su veličine
povezane Avogadrovom konstantom, .
Brojčana vrijednost Avogadrove konstante jednaka je Avogadrovu broju, ali ima jedinicu mol–1.
Brojnost i množina tvari proporcionalne su veličine povezane Avogadrovom konstantom, .
Brojčana vrijednost Avogadrove konstante jednaka je Avogadrovu broju, ali ima jedinicu mol–1.

Avogadrov broj
Amedeo Avogadro, punim imenom Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto, talijanski je fizičar i kemičar (1776 – 1856).
U njegovu čast broj osnovnih čestica plina, koji sadrži 1 mol, naziva se Avogadrov broj i iznosi čestica.
Prvi ga je u stvari izračunao Johann Josef Loschmidt pa se u njemačkom govornom području naziva i Loschmidtov broj.
Godine 1811. Amedeo Avogadro postavio je Avogadrov zakon, koji vrijedi za idealne plinove. Prema tom zakonu jednaki volumeni različitih plinova pri istom tlaku i temperaturi sadrže jednak broj molekula.
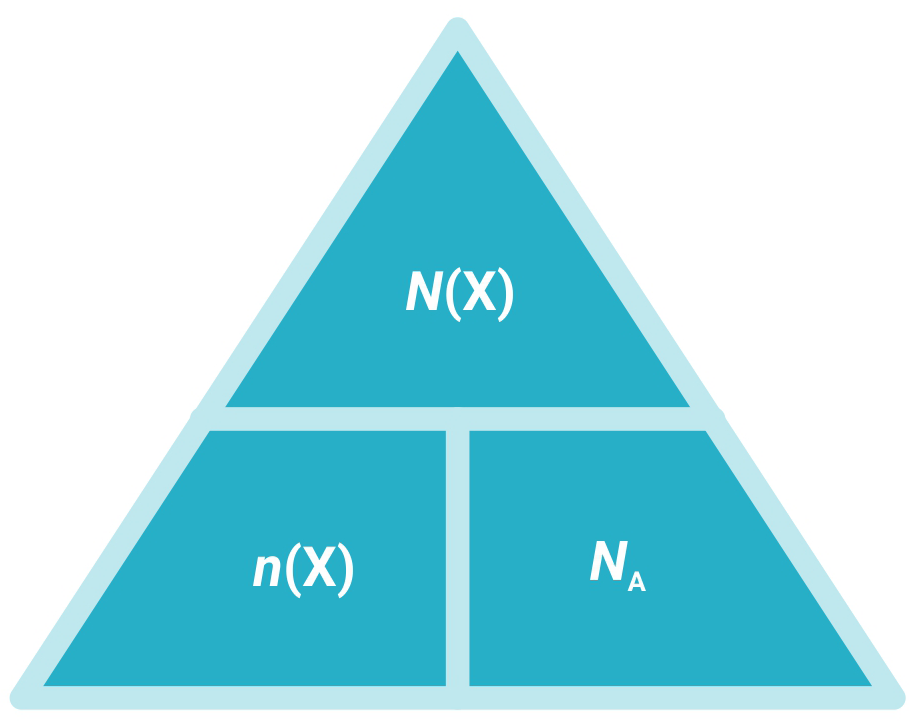
Budući da Avogadrov broj predstavlja skup istovrsnih jedinki, a množina označava brojnost tih skupova, njihov međusobni odnos dan je izrazom:
|
|
 |
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Želite li pokušati ponovo?
Molarna masa
Molarna masa, M, fizikalna je veličina koja povezuje masu i množinu tvari.
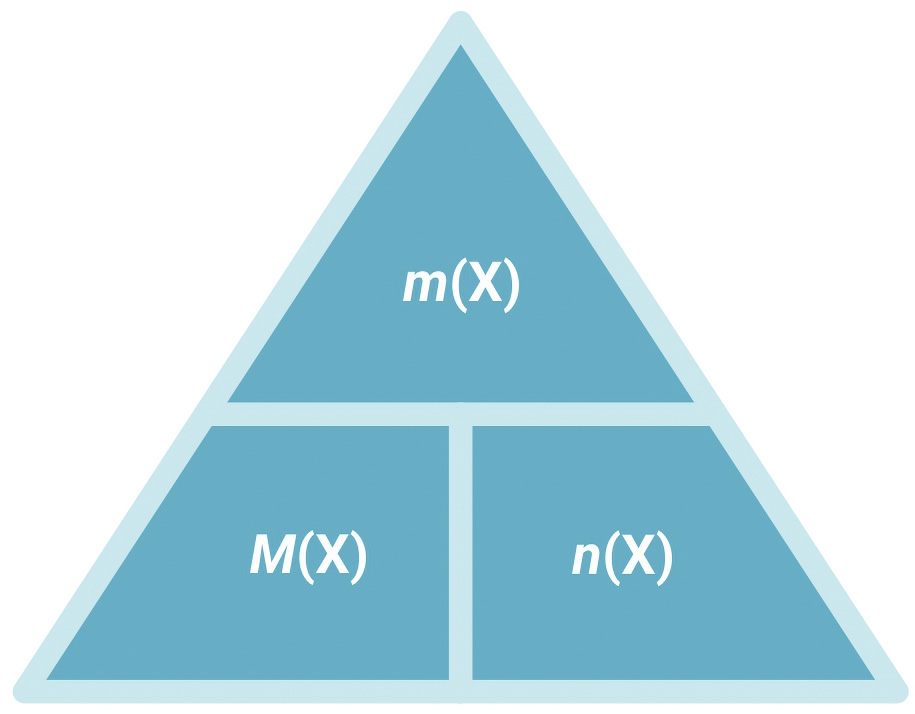 |
Iz izraza za molarnu masu proizlazi da je:
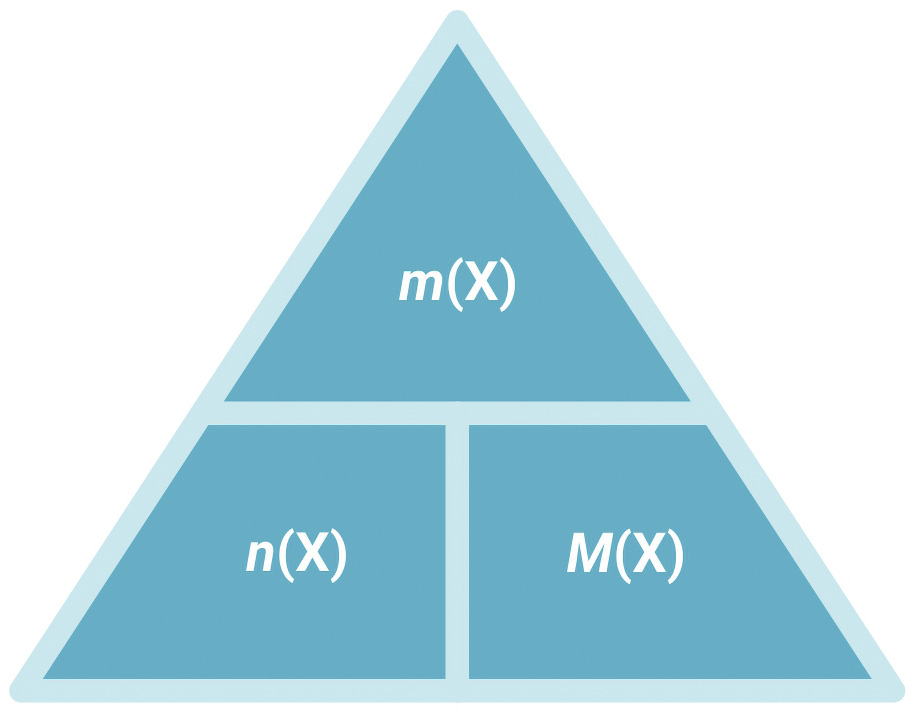 |
Brojčana vrijednost molarne mase jednaka je brojčanoj vrijednosti relativne atomske ili molekulske mase iskazane u g mol–1.
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Želite li pokušati ponovo?
Riješeni primjer 1.
Prakilogram izrađen je krajem 19. stoljeća, davne 1889. godine, kao legura 90 % platine i 10 % iridija. Znanstvenici i danas nemaju odgovor na pitanje kako je moguće da takav materijal gubi na masi. Nakon gotovo stotinu godina, 1988. godine, utvrđeno je da je prakilogram iz Sevresa lakši za 0,05 miligrama (50,0 μg) od svojih replika. To je otprilike masa zrna pijeska.
Izračunajte broj atoma platine i broj atoma iridija koji je izgubio prakilogram.
Zadano je:
50,0 μg
90,0 %
10,0 %
45,0 μg
5,00 μg
Traži se:
Izračun:
Odgovor:
Prakilogram je u posljednjih stotinu godina izgubio atoma platine i atoma iridija.
Molarni volumen plina
Jedan od prvih znanstvenika koji je ispitivao ponašanje plinova
bio je francuski prirodoslovac Joseph L. Gay-Lussac.
On je početkom 19. stoljeća otkrio zakon volumnih omjera.
Omjeri volumena plinova koji međusobno reagiraju
ili nastaju kemijskom reakcijom jesu mali cijeli brojevi.
To vrijedi ako se mjerenja izvode pri stalnome tlaku i temperaturi.
Molarni volumen plina
Jedan od prvih znanstvenika koji je ispitivao ponašanje plinova bio je francuski prirodoslovac Joseph L. Gay-Lussac. On je početkom 19. stoljeća postavio zakon volumnih omjera: Omjeri volumena plinova koji međusobno reagiraju ili nastaju kemijskom reakcijom jesu mali cijeli brojevi, ako se mjerenja izvode pri stalnome tlaku i temperaturi.
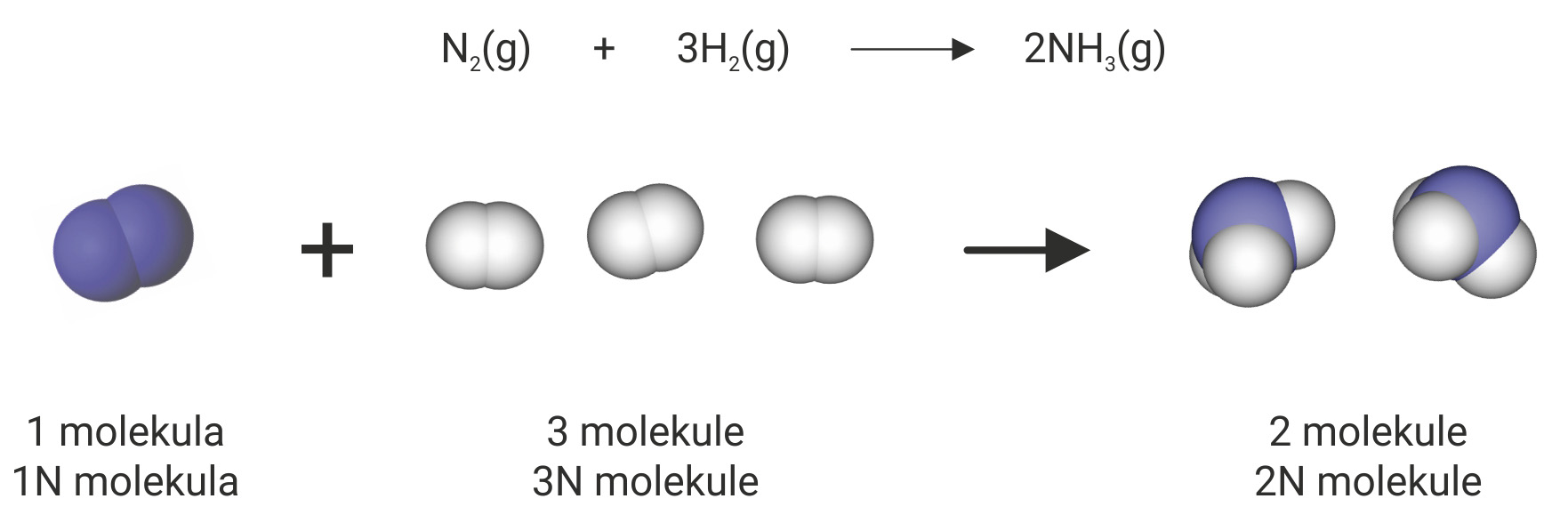
Plinovi jednakih volumena pri istoj temperaturi i tlaku sadržavaju jednak broj čestica, pa prema tomu i jednake množine.
Jedna molekula dušika spajanjem s tri molekule vodika daje dvije molekule amonijaka. Iz toga slijedi da se jedan volumen dušika spaja s tri volumena vodika, pri čemu nastaju dva volumena amonijaka, jer jednak broj molekula bilo kojega plina pri jednakim uvjetima zauzima jednake volumene.
Volumen 1 mola bilo kojega plina pri tlaku od 101 325 Pa i
temperaturi 0 °C (normalni uvjeti) uvijek je isti i iznosi 22,4 litre. Taj se volumen naziva molarni volumen plina, , a mjerna jedinica je . Definiran je izrazom:
|
pri i 0 °C |
–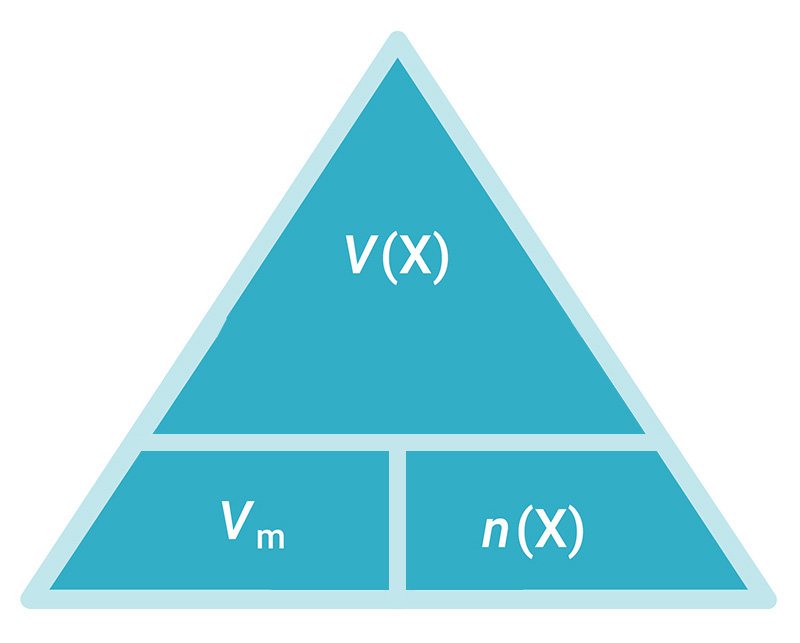 |
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Želite li pokušati ponovo?
Poznato vam je da jedan mol plina pri normalnim uvjetima ima volumen od . Ako uvjeti nisu normalni, volumen plina računa se prema općoj plinskoj jednadžbi:
gdje je:
p – tlak
V – volumen plina
n – množina plina
T – temperatura
R – opća plinska konstanta, ili
Riješeni primjer 2.
U posudi volumena 750 mL nalazi se dušik pri temperaturi 20 °C i tlaku 115 kPa. Izračunajte molarnu masu, množinu, masu i brojnost molekula dušika.
Zadano je:
t = 20 °C
p = 115 kPa
p = 115 000 Pa
Traži se:
Korak 1
Odgovor:
Molarna masa molekule dušika je 28,02 g mol-1.
Korak 2
iz toga slijedi da je množina molekula dušika:
Odgovor:
Množina molekula dušika je 0,0354 mol.
Korak 3
Odgovor:
Masa molekula dušika je 0,992 g.
Korak 4
Odgovor:
Brojnost molekula dušika je 2,13 × 1022.
Izračunajte molarnu masu plina ako 1,96 g plina pri temperaturi od 27 °C i tlaku od 97 300 Pa zauzima volumen od 1,25 dm3.
Rješenje:
Molarna masa plina je .
Izračunajte gustoću kisika pri 25 °C i 97,0 kPa. Gustoću kisika iskažite u g dm–3.
Rješenje:
Gustoću izrazite iz izraza za opću plinsku jednadžbu.
Gustoća kisika pri 25 °C i iznosi .
Prigodni optjecajni kovani novac od 25 kuna
Sastav kovina
Prigodni optjecajni kovani novac od 25 kuna
izrađen je od dvodijelne kovine.
Jezgra zlatnoga sjaja sastoji se od
slitine 92 % bakra, 6 % aluminija i 2 % nikla.
Prsten je izgrađen od slitine srebrnasta sjaja
koja se sastoji od 75 % bakra i 25 % nikla.
Promjer i težina
Prigodni optjecajni kovani novac od 25 kuna
ima oblik pravilnoga dvanaesterokuta.
Promjer opisane kružnice iznosi 32 milimetra.
Masa je toga prigodnoga novca 12,75 grama.
Jezgra ima promjer 18 milimetara i masu 4,05 grama.
Prsten ima unutarnji promjer 18 milimetara i masu 8,70 grama.
Prigodni optjecajni kovani novac od 25 kuna
Sastav kovina
Prigodni optjecajni kovani novac od 25 kuna izrađen je od dvodijelne kovine. Jezgra zlatnoga sjaja sastoji se od slitine 92 % bakra, 6 % aluminija i 2 % nikla, a prsten od slitine srebrnasta sjaja sastoji se
od 75 % bakra i 25 % nikla.
Promjer i težina
Kovanica od 25 kuna ima oblik pravilnoga dvanaesterokuta, kojemu promjer opisane kružnice iznosi 32 milimetra. Masa toga prigodnoga novca iznosi 12,75 grama. Jezgra ima promjer 18 milimetara i masu 4,05 grama. Prsten ima unutarnji promjer 18 milimetara i masu 8,70 grama.
Na temelju podataka u tekstu popunite tablicu i izračunajte broj atoma bakra u kovanici od 25 kuna.
| jezgra | prsten |
|---|---|
| w1(Cu) = _____________% | w2(Cu) = _____________% |
| w(Al) = ______________% | w(Ni) =______________% |
| w(Ni) =______________% |
Ukupna masa kovanice je _____________ g.
Masa jezgre je ____________ g.
Masa prstena je ____________ g.
Traži se:
Masa bakra u jezgri kovanice = ?
Masa bakra u prstenu kovanice = ?
Korak 1
Korak 2
Korak 3
Odgovor:
U kovanome novčiću od 25 kuna nalazi se atoma bakra.
Na kraju…
Unesite odgovore na pripadajuća mjesta.
Unesite odgovore na pripadajuća mjesta.
Klikom odaberite jedan točan odgovor.
Odaberite točan odgovor.
Koliko mola magnezijeva fosfata, , sadržava 0,2500 mola atoma kisika?
Unesite odgovore na pripadajuća mjesta.
Želite li pokušati ponovo?