

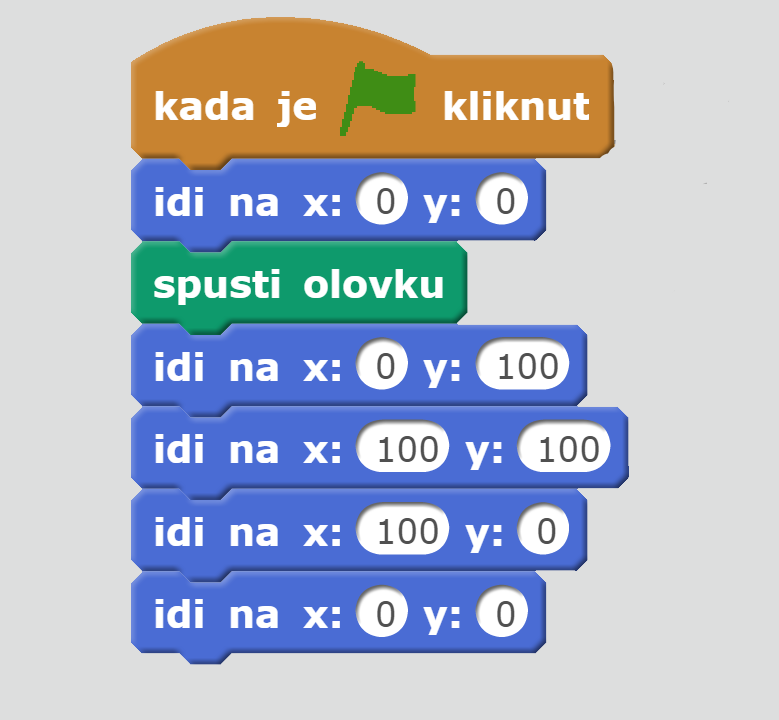
Koordinatni sustav u ravnini važan je i u programiranju jer koordinate omogućuju postavljanje likova i stvari na točno određeno mjesto na zaslonu. Na ovoj slici možete vidjeti primjer crtanja kvadrata u Scratchu. Kvadrat je zadan koordinatama svojih vrhova koje su redom i Razmislite zašto je olovka za crtanje spuštena tek nakon što je lik postavljen na vrh
Pokušajte i vi u Scratchu nacrtati neki geometrijski lik uporabom koordinata njegovih vrhova. Najprije nacrtajte pravokutnik i trokut. Zatim pokušajte nacrtati neki složeniji lik. Isprobajte okruženje za pisanje programa u Scratchu.
Ako vam zatreba pomoć, pročitajte Vodič za korisnice i korisnike.
Više informacija, različite upute i projekte pronaći ćete na glavnim stranicama Scratcha (stranice su djelomično dostupne na hrvatskom jeziku). Usporedite svoje programe s programima ostalih učenika te razmijenite savjete o tome kako napisati pregledan i učinkovit računalni program. Ako poznajete neke druge programske jezike, istražite kako se u njima pišu naredbe za pomicanje na mjesto određeno koordinatama.
Za uvježbavanje i samostalno istraživanje koordinatnog sustava u ravnini predlažemo vam nekoliko zadataka koje možete samostalno riješiti u bilježnici uporabom digitalnog predloška koordinatnog sustava ili u nekoj aplikaciji za dinamičnu matematiku, kao što su GeoGebra ili Desmos. Nakon što riješite zadatak, usporedite svoje rješenje s rješenjima ostalih učenika. Podijelite svoje znanje s njima ili ih zamolite da vama pomognu ako vam je neki zadatak težak.
U koordinatnom sustavu na pravcu pronađite točke Zadatak možete riješiti i koristeći se digitalnim predloškom koordinatnog sustava izrađenim u GeoGebri.
U koordinatnom sustavu na pravcu što točnije odredite točke
U koordinatnom sustavu na pravcu odredite približno mjesto točaka
U pravokutni koordinatni sustav ucrtajte točke
i spojite ih abecednim redom. Zatim spojite i točke
i
Nakon toga podebljajte točku
i spojite je redom s točkama
i
Podebljajte još i točke
i
Koji lik ste dobili?
Zadatak možete riješiti i koristeći se digitalnim predloškom koordinatnog sustava izrađenim u GeoGebri.
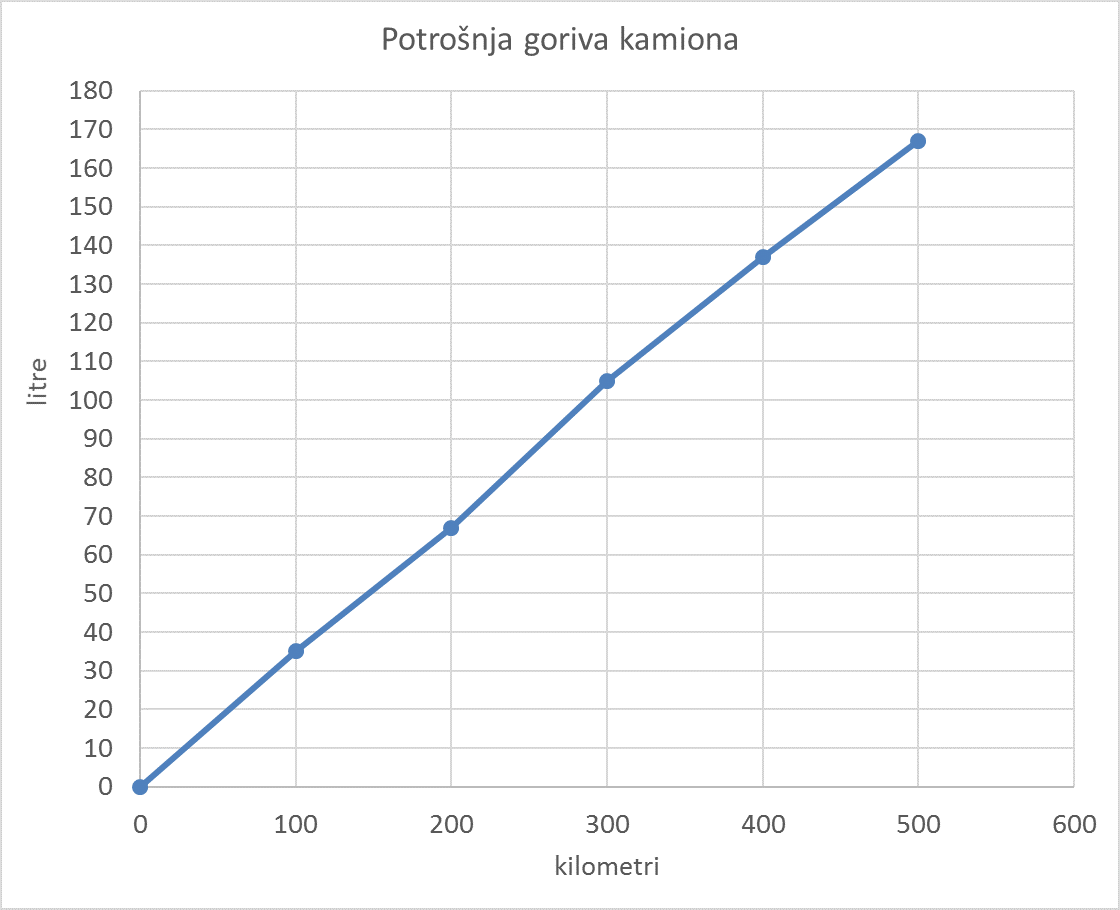
Pogledajte grafički prikaz na slici pa očitavanjem koordinata odgovorite na postavljena pitanja.
Napišite sve uređene parove cijelih brojeva kojima je umnožak prvoga i drugog člana jednak
Pomoć:
Brojčano rješenje upišite u za to predviđen prostor.
Očitajte točke ucrtane u pravokutni koordinatni sustav.
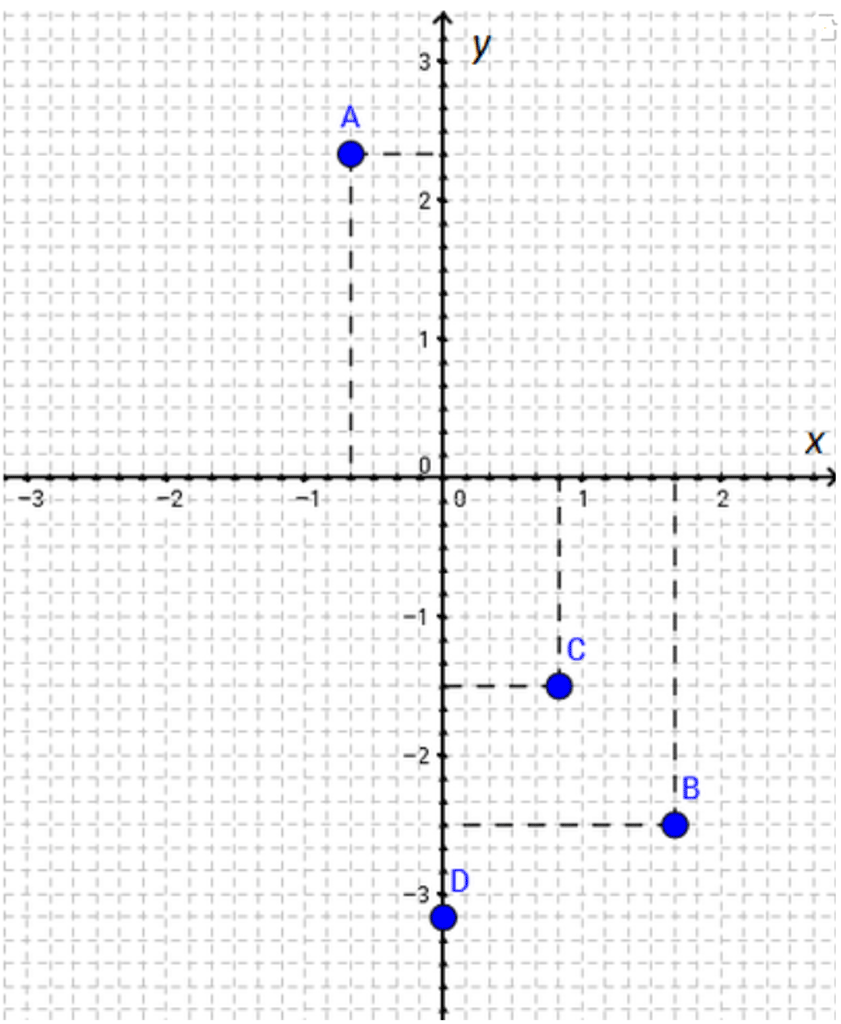
Koordinate točaka su
Ucrtajte točke u pravokutni koordinatni sustav.
Zadatak možete riješiti i koristeći se digitalnim predloškom koordinatnog sustava izrađenim u GeoGebri.
Kvadrat zadan je koordinatama triju svojih vrhova: Procijenite koordinate četvrtog vrha, zadanog kvadrata i ucrtajte taj kvadrat u pravokutni koordinatni sustav.
Rješenje upišite u obliku cijeloga ili decimalnog broja s jednom decimalom.
Pomoć:
Brojčano rješenje upišite u za to predviđen prostor. Rješenje upišite u obliku cijelog ili decimalnog broja s jednom decimalom.
Pomoć:
Procijenite rješenje. Rezultat upišite u obliku cijelog broja na za to predviđeno mjesto.
Odredite nepoznate elemente tako da vrijedi:
Nepoznati su elementi:
Odredite nepoznate elemente tako da vrijedi:
Nepoznati su elementi:
Riješite.
Zadan je pravokutni trokut
površine
kvadratnih jedinica. Pravi kut toga trokuta smješten je u ishodište koordinatnog sustava, a koordinate točke
su
Odredi koordinate točke
Koliko rješenja ima zadatak?
Najprije nacrtajte sve u pravokutnome koordinatnom sustavu, odredite duljinu jedne katete sa slike, izračunajte duljinu nepoznate katete pravokutnog trokuta s pomoću formule za površinu pravokutnog trokuta i zaključite da se točka nalazi na osi Zadatak ima dva rješenja:
Točka je vrh nasuprot osnovici jednakokračnog trokuta površine kvadratnih jedinica. Koordinate rubnih točaka osnovice tog trokuta su i Odredite koordinate točke
Zadatak ima dva rješenja:
i
Za detaljan postupak pogledajte video.
Pomoć:
Riješenje upišite u brojčanom obliku na za to predviđena mjesta.
Pomoć:
Dijametralno suprotne točke su rubne točke promjera ili dijametra.
Brojčani rezultat upišite u obliku cijeloga ili decimalnog broja s jednom decimalom na za to predviđeno mjesto.
Procijenite koje bi bile koordinate četvrte točke, paralelograma kojemu su koordinate triju točaka i ucrtajte sve u pravokutni koordinatni sustav.
Kad ucrtate točke u pravokutni koordinatni sustav, uočite za koliko je jediničnih duljina po os apscisa točke udaljena od apscise točk Jednako toliko po os mora biti udaljena i apscisa točke od apscise točke Zaključak o ordinatama donesite sami. Koordinate četvrtog vrha su
Kvadrat zadan je koordinatama susjednih vrhova: i Procijenite koordinate vrhova i zadanog kvadrata i ucrtajte taj kvadrat u pravokutni koordinatni sustav. Koliko je mogućih rješenja?
Ucrtajte u pravokutni koordinatni sustav i riješite.
Pomoć:
Površinu pravokutnog trokuta računamo prema formuli gdje su a i b duljine kateta toga trokuta.
Rezultat zapišite u obliku cijelog broja na za to predviđeno mjesto.
U pravokutnome koordinatnom sustavu zadan je trokut svojim vrhovima i Dovucite vrhove osnosimetrične slike trokuta s obzirom na os apscisa, na pripadajuće koordinate.
|
|
|
|
|
|
|
|
Pomoć:
Pažljivo pročitajte zadatak
i nacrtajte sliku u pravokutnom koordinatnom sustavu