3.8 Jednoliko gibanje po kružnici

Opis jednolikoga gibanja po kružnici

Na gramofonu se ploče (vinili) okreću $33$ ili $45$ okretaja u minuti. Kako ćemo odrediti period vrtnje $T,$ tj. vrijeme potrebno da ploča napravi puni krug ako smo je postavili na $45$ okretaja?

Izračunat ćemo tako da vremenski interval od $60$ s podijelimo na $45$ dijelova.

$T=\frac{60}{45}\mathrm{s}$

$T=\mathrm{1,33}\mathrm{s}$ 

Mjerna jedinica za frekvenciju je herc ( $\mathrm{Hz}$).

U našem primjeru:

$f=\frac{3}{4}\mathrm{Hz}$ 

$f=\mathrm{0,75}\mathrm{Hz}.$

Na fotografiji je kotač Markova bicikla. Marko krene u vožnju. Na dijelu puta gdje je vozio stalnom brzinom kotač se okrenuo $20$ puta u $10$ sekundi. Kolika je frekvencija i koliki je period vrtnje kotača?

Jednostavnim računanjem dobijemo:

$f=2\mathrm{Hz}$ 

$T=\mathrm{0,5}\mathrm{s}.$

Kako bismo odredili kolika je brzina kojom tzv. mačje oko na kotaču prolazi kružnu putanju?

$v=\frac{2·r·\pi }{T}$

ili

$v=2·r·\pi ·f.$

Osim nje možemo izračunati i kutnu brzinu.

$\omega =\frac{\Delta \phi }{\Delta t}$

Mjerna jedinica za kutnu brzinu je radijan u sekundi ( ${\mathrm{rads}}^{-1}$).

Za vrijeme jednog perioda ( $T$) polumjer će napraviti kut $2\pi$ radijana.

Prema tome pisat ćemo:

$\omega =\frac{2\pi }{T}$

$\omega =2·\pi ·f.$

Obodna i kutna brzina povezane su izrazom:

$v=r·\omega .$

Primjer 1.

Odredimo sada obodnu i kutnu brzinu kojom je tzv. mačje oko na Markovu biciklu kružilo oko središta kotača na dijelu puta na kojem se kotač okretao frekvencijom $2\mathrm{Hz}.$ Mačje je oko udaljeno $20\mathrm{cm}$ od središta rotacije kotača.

Rješenje

---

Centripetalna akceleracija i sila

Obodna je brzina tijela, čija smo gibanja promatrali u prethodnim primjerima, prema iznosu stalna, ali u svakom trenutku mijenja smjer. Takvo gibanje nazivamo jednoliko gibanje po kružnici.

Pokus

Izvedite jednostavan pokus te raspravite o njemu sa svojim prijateljima.

Uzmite čvrst konac ili tanko uže te na jedan njegov kraj privežite kolut ljepljive vrpce (selotejpa). Jednom rukom držite slobodan kraj užeta, a drugom zavrtite kolut iznad glave kao na slici.

Raspravite:

Kakvo gibanje izvodi tijelo na užetu? Što bi se dogodilo kada bismo pustili donji kraj užeta? Koja sila djeluje na tijelo pri kružnom gibanju? U kojem smjeru i koja joj je orijentacija? Što bi se dogodilo kada bi konac puknuo?

Promijenite masu tijela tako da umjesto jednog privežete dva koluta, a zatim tri, te polumjer kružnice po kojoj se tijelo giba pa pokušajte okretati tijelo tako da se giba jednakom obodnom brzinom. Što primjećujete?

U pokusu koji ste izveli tijelo privezano na konac gibalo se jednoliko po kružnici. Sila napetosti niti koja je uzrokovala kružno gibanje utega bila je cijelo vrijeme usmjerena prema središtu vrtnje. Kada bi ona prestala djelovati, tijelo bi bilo izbačeno horizontalno po tangenti na kružnu putanju. Iz pokusa ste mogli zaključiti da ta sila ovisi o masi tijela, obodnoj brzini te polumjeru kružne putanje po kojoj se tijelo giba.

 

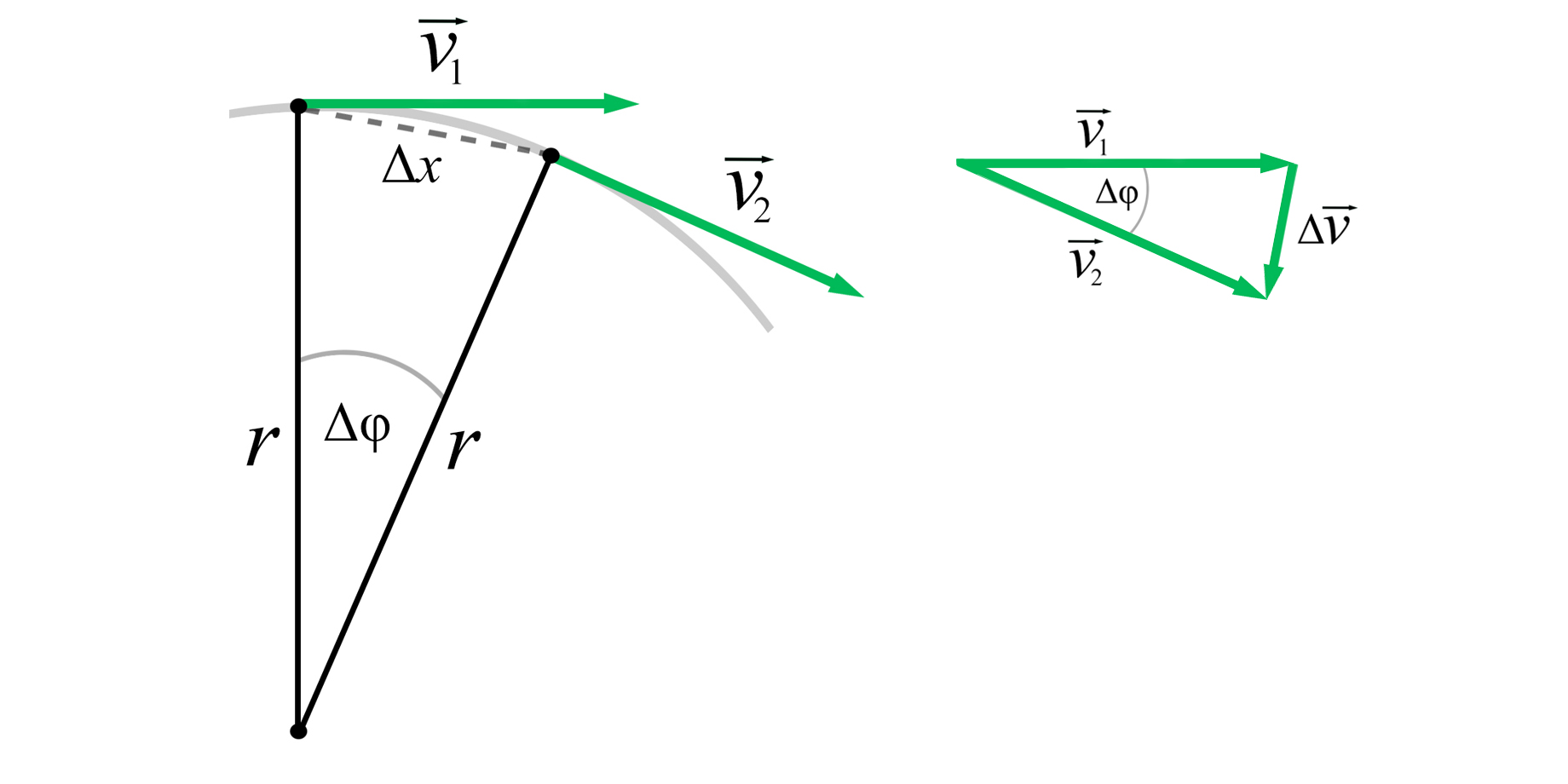
Pri jednolikom gibanju po kružnici mijenja se smjer brzine.

Centripetalna akceleracija je promjena vektora obodne brzine u vremenskom intervalu:

$\stackrel{\to }{a}=\frac{\mathrm{\Delta }\stackrel{\to }{\mathrm{v}}}{\Delta t}$ 

Kada tijelo pri kružnoj putanji prijeđe dio kružnog luka tako da polumjer $r$ napravi kut, pomak tijela iznosi $x.$ Ako je kut dovoljno malen, pomak je približno jednak prijeđenom kružnom luku. K tome je trenutačna obodna brzina okomita na polumjer, koji spaja središte zakrivljenosti s položajem tijela pa su trokuti na slikama slični.

Možemo pisati:

$\frac{\mathrm{\Delta }\stackrel{\to }{v}}{v}=\frac{\Delta x}{r},$ tj.:

$\mathrm{\Delta }\stackrel{\to }{v}\mathrm{=}v\mathrm{·}\frac{\mathrm{\Delta }\stackrel{\to }{x}}{r}.$

Uvrštavajući u izraz za iznos centripetalne akceleracije dobijemo:

$a_{cp}=\frac{v·\mathrm{\Delta }x}{r·\mathrm{\Delta }t}$

$a_{cp}=\frac{v^2}{r}$

Primjenjujući drugi Newtonov zakon, dobijemo izraz za iznos centripetalne sile:

$F_{cp}\mathrm{=}m·\frac{v^2}{r}$

U pokusu o kojem smo govorili napetost niti bila je centripetalna sila. Ali centripetalna sila je bilo koja sila koja tijelo drži na zakrivljenoj putanji.

U slučaju geostacionarnog satelita, čije je gibanje oko Zemlje prikazano na sljedećoj animaciji, centripetalna sila je gravitacijska sila između satelita i Zemlje. Pogledajte animaciju u kojoj je prikazano gibanje geostacionarnog satelita oko Zemlje, a posebno promatrajte smjer i orijentaciju obodne brzine, centripetalne sile i centripetalne akceleracije.

Povezani sadržaji

Ako ste zaboravili značenje pojmova radijalno i tangencijalno, podsjetite se što ste o kružnici učili iz Matematike.

Zbog čega je vožnja u zavojima pri poledici opasnija nego po suhoj cesti?

Gibajući se u zavoju, automobil je na kružnoj putanji.

Koja je sila u tom slučaju centripetalna?

U zavoju je sila trenja između kotača i ceste centripetalna pa će brzina kojom možemo sigurno proći zavoj ovisiti o polumjeru zakrivljenosti zavoja (njegovoj „oštrini”) i faktoru trenja.

Pogledajte interaktivni element i pokušajte automobil u njemu sigurno provesti zavojem.

Povezani sadržaji

Prisjetite se što ste iz Prometne kulture govorili o vožnji s obzirom na različite uvjete na cesti.

Kutak za znatiželjne

Analizirajte kružno gibanje na primjeru iz stvarnog života s pomoću programa Tracker. Primjer odaberite sami. To može biti gibanje sitnog predmeta na gramofonskoj ploči, tzv. mačjeg oka na kotaču bicikla… Snimite film. Analizirajte gibanje s pomoću programa Tracker i odgovorite na pitanja, tj. riješite zadatke.

O kakvu se gibanju radi? Objasnite zaključak?

Odredite:

• period i frekvenciju gibanja
• obodnu brzinu
• kutnu brzinu
• centripetalnu akceleraciju
• centripetalnu silu.

Uz istu frekvenciju kružnoga gibanja i masu tijela ispitajte ovisnost navedenih veličina o polumjeru putanje i nacrtajte na papiru odgovarajuće dijagrame.

Uz istu frekvenciju kružnoga gibanja i polumjer ispitajte ovisnost navedenih veličina o masi tijela i nacrtajte odgovarajuće dijagrame.

Osmislite mjerenje s pomoću kojeg ćete dobiti jednake podatke bez uporabe programa Tracker.

Rezultate prikažite u jednom od alata za interaktivnu prezentaciju, npr. Prezi, Genial.ly ili Piktochart.