

Što su logaritmi i zašto ih trebamo?
Ivo je dobio novac od bake, mame, tate, tete...
Za kupovinu novog računala Ivo ipak nema dovoljno novca. Odlučio je pohraniti novac u banci. U banci su mu rekli da je kamata
godišnje. Ivo sada želi znati kada će imati dovoljno novca za kupovinu računala. U školi je naučio eksponencijalnu funkciju i pokušao je svoj problem riješiti, ali ipak treba još ponešto naučiti.
U prošloj jedinici naučili ste crtati graf eksponencijalne funkcije.
Nacrtajte graf funkcije
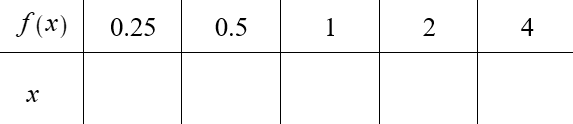
Za pomoć vam može poslužiti sljedeća tablica:
U prošlom ste zadatku za zadani argument određivali vrijednost funkcije
Popunite tablicu tako da za zadanu vrijednost funkcije odredite argument.
Kako ste riješili prošli zadatak?
Mogli ste to napraviti na dva načina:
Odgovor je
Taj broj zovemo logaritam.
Logaritam
Logaritam broja po bazi jest eksponent kojim treba potencirati zadanu bazu da bi se dobio Dakle,
ako je onda je
Primjer 1.
Izračunajmo.
zato što je
zato što je
zato što je
Vidjeli smo da su potencije i logaritmi povezani. Postoje li pravila za računanje s logaritmima koja su slična pravilima za računanje s potencijama?
Pravila za računanje s logaritmima
zato što je
zato što je
(pravilo umnoška)
(pravilo potencije)
(pravilo kvocijenta)
Koristeći se navedenim pravilima odgovorite na sljedeća pitanja i provjerite jeste li pravila razumjeli.
Ako je i onda je
Primjer 2.
Primijenimo pravila za računanje s logaritmima na sljedećim zadatcima.
Povežite odgovarajuće parove.
|
|
|
|
|
|
|
|
|
|
|
Primjer 3.
U sljedećem videu pogledajte jedan složeniji primjer.
Zašto su pravila za računanje s logaritmima važna?
Pogledate li pažljivo pravilo umnoška, primijetit ćete da je na jednoj strani množenje, a na drugoj zbrajanje. S pomoću te jednadžbe množenje se svodi na zbrajanje. Do razvoja računala to je bio jedan od uobičajenih načina množenja velikih brojeva.
Nekoliko je imena koje treba spomenuti u vezi s izradom prvih mehaničkih pomagala za računanje osnovnih aritmetičkih operacija - Johna Napier (1550. - 1617.) i William Oughtred (1574. - 1660.).
John Napier objavio je prve logaritamske tablice, a Oughtred 1622. godine izrađuje logaritamsko računalo.
Od 1654. godine u uporabi su ravna logaritamska računala, poznata pod nazivom pomično računalo ili "šiber". Pravilo koje smo spomenuli na početku upravo je jedno od onih koja se koriste prilikom primjene "šibera".
Pred vama je slagalica. Ispod slagalice nalaze se kartice s rješenjima. Postavljajući ispravno rješenje na zadatak otkrivat ćete polja fotografije prvog računala.