

U laboratoriju se nalazi uzorak bakterija za analizu. U uzorku ima bakterija. Ako se bakterije razmnožavaju tako da se njihov broj udvostruči svakih minuta, koliko će bakterija biti u uzorku nakon: a) minuta, b) minuta, c) sat, d) sata? Možete li povećanje broja bakterija prikazati grafički? Odredite funkciju koja opisuje porast broja bakterija s obzirom na vrijeme.
Početna vrijednost iznosi
komada. Nakon
minuta bit će
bakterija, nakon
minuta
bakterija, nakon
sata
bakterija...
Ako se bakterije dupliciraju, tada je porast eksponencijalan s bazom
Funkcija koja opisuje porast broja bakterija tijekom vremena glasi pri čemu je broj dupliciranja, tj. broj vremenskih odsječaka od minuta.
Nakon sata, dijeljenja bakterija, broj bakterija bit će:
Nakon sata, dijeljenja bakterija, broj bakterija bit će:
Nakon kojeg će se vremena broj bakterija povećati na Možete li grafički prikazati ovisnost vremena o broju bakterija? Možete li odrediti funkciju koja za zadani broj bakterija daje koliko je puta provedena dioba?
Odgovore na ova i slična pitanja dobit ćete u nastavku.
Eksponencijalna funkcija jest funkcija oblika
Domena eksponencijalne funkcije jest skup
Kod eksponencijalne funkcije za svaki poznati
koji je element slike pokušajmo odrediti
koji se u njega preslikava. Znači iz
određujemo
i dobivamo
Dobili smo logaritamsku funkciju koja je definirana na svim elementima slike polazne eksponencijalne funkcije.
Domena logaritamske funkcije jednaka je
Logaritamska funkcija s bazom
realna je funkcija oblika
pri čemu je
i
. Domena logaritamske funkcije skup je pozitivnih realnih brojeva
Skup njezinih vrijednosti jest cijeli skup
Logaritamsku funkciju s bazom zapisujemo
Logaritamsku funkciju s bazom
zapisujemo
Eksponencijalne i logaritamske funkcije kao argument mogu imati i neku funkciju s varijablom
ili se mogu dobiti nekim računskim operacijama nad elementarnom funkcijom. U tom se slučaju mogu promijeniti neka svojstva elementarne eksponencijalne ili logaritamske funkcije.
Rasporedite funkcije prema vrsti.
Stavimo li kao argument logaritamske funkcije izraz koji uz sadrži još nešto, možemo promijeniti domenu logaritamske funkcije.
Primjer 1.
Odredimo domenu funkcije
Logaritam možemo računati za strogo pozitivne brojeve. Stoga je potrebno da je Domena ove funkcije jest
Odredite domene sljedećih funkcija:
Postoje li logaritamske funkcije kojima skup vrijednosti nije cijeli skup
Odredite vrijednost funkcije
za zadane argumente.
Pogledajmo kako izgleda graf logaritamske funkcije.
U tablicu unesite vrijedosti funkcije za istaknute argumente te iscrtajte graf logaritamske funkcije
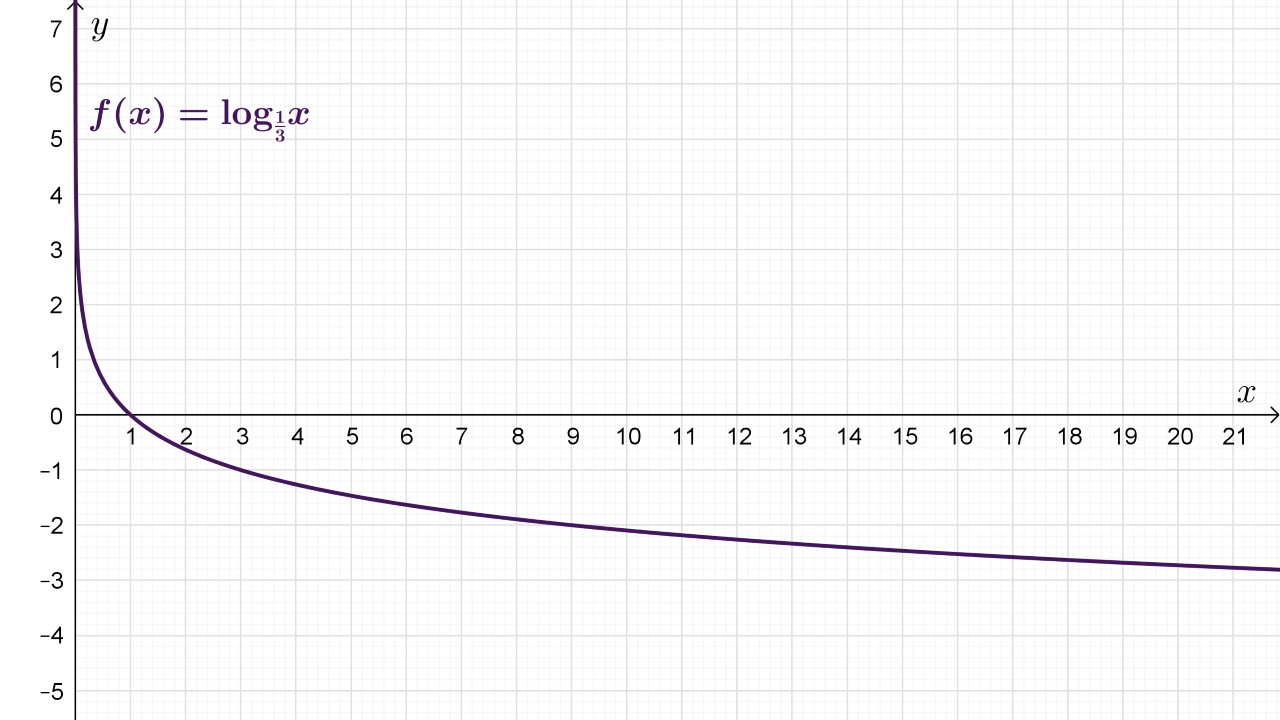
Nacrtajte graf logaritamske funkcije
Kao pomoć može vam poslužiti tablica s vrijednostima argumenata.
Koja tvrdnja vrijedi za eksponencijalnu funkciju
Kojom točkom prolazi graf eksponencijalne funkcije ?
Što vrijedi za logaritamsku funkciju
Kojom točkom prolazi graf logaritamske funkcije
Istražimo sada kako baza logaritamske funkcije utječe na izgled grafa funkcije.
Mijenjajte bazu logaritamske funkcije pa riješite sljedeće zadatke.
Što je baza logaritamske funkcije veća, to su vrijednosti logaritamske funkcije
Kako izgleda graf logaritamske funkcije
s obzirom na bazu?
Logaritamska funkcija za različite argumente daje različite vrijednosti.
Logaritamska funkcija strogo je rastuća za tj. za vrijedi
Logaritamska funkcija strogo je padajuća za tj. za vrijedi
Logaritamska funkcija
jest injektivna, tj. iz
slijedi
Logaritamska funkcija može biti ili strogo rastuća ili strogo padajuća. Monotonost ovisi o bazi logaritamske funkcije.
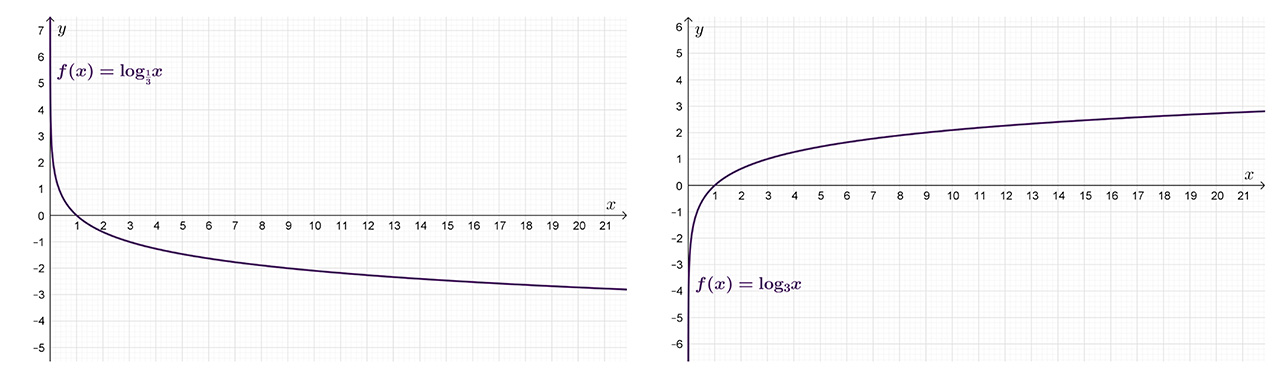
Pogledajmo sada sva svojstva logaritamske funkcije.
Graf logaritamske funkcije može imati nultočku različitu od Nacrtajte grafove funkcija:
Graf logaritamske funkcije može imati pomak po osi. Nacrtajte grafove funkcija:
Mijenjajući koeficijente
istražite izgled grafa logaritamske funkcije
Svoja zapažanja možete prezentirati učenicima u razredu ili napraviti plakat.
Rasporedite svojstva eksponencijalne i logaritamske funkcije u
skupine: ona koja vrijede samo za eksponencijalnu funkciju, ona koja vrijede samo za logaritamsku funkciju i svojstva koja vrijede za obje funkcije.
Svojstva eksponencijalne i logaritamske funkcije