Matematika 3 - 9.2 Opći oblik jednadžbe kružnice

Na početku...

Kružnice u prirodi

Kružnicu možemo zadati jednadžbom ili grafički. Za jedan i drugi oblik potrebni su nam središte i polumjer. Iz jednadžbe

{(x - p)}^{2} + {(y - q)}^{2} = r^{2}

${(x - p)}^{2} + {(y - q)}^{2} = r^{2}$ lako iščitamo koordinate središta

S (p, q)

$S (p, q)$ i polumjer kružnice

r .

$r .$

Jednadžba i graf kružnice

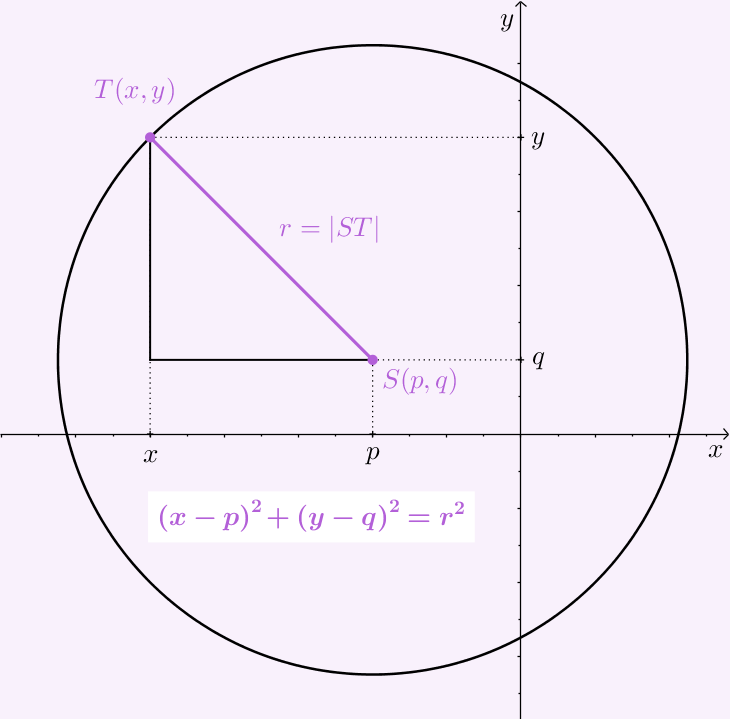
Iz grafičkog prikaza očitamo koordinate središta i jedne točke na kružnici i izračunamo njihovu udaljenost kako bismo dobili polumjer kružnice.

Što ako nam kružnica nije zadana tako da odmah možemo iščitati koordinate i polumjer?

Opći oblik jednadžbe kružnice

Opći je oblik jednadžbe kružnice

$x^{2} + y^{2} + A x + B y + C = 0, A, B, C \in R .$ $x^{2} + y^{2} + A x + B y + C = 0, A, B, C \in R .$

Uočite da je uz $x^{2} i y^{2}$ $x^{2} i y^{2}$ koeficijent $1 .$ $1 .$ Jedino u tom obliku takva jednadžba može biti jednadžba kružnice. Kako tako zadanoj kružnici odrediti koordinate središta i polumjer?

Prisjetimo se najprije formule za kvadrat binoma.

Složite formule za kvadrat zbroja i kvadrat razlike.

${(x + y)}^{2} =$ ${(x + y)}^{2} =$	$x^{2} - 2 x y + y^{2}$ $x^{2} - 2 x y + y^{2}$
${(x - y)}^{2} =$ ${(x - y)}^{2} =$	$x^{2} + 2 x y + y^{2}$ $x^{2} + 2 x y + y^{2}$

null

Svaku stranu dobivenih formula imenujte.

$x^{2} \pm 2 x y + y^{2}$ $x^{2} \pm 2 x y + y^{2}$	kvadrat binoma
${(x \pm y)}^{2}$ ${(x \pm y)}^{2}$	potpun kvadrat

null

Primjer 1.

Odredimo koordinate središta i polumjer kružnice $x^{2} + y^{2} + 4 x - 2 y - 13 = 0 .$ $x^{2} + y^{2} + 4 x - 2 y - 13 = 0 .$

Pogledajte animaciju kako, svođenjem na potpun kvadrat, opći oblik jednadžbe kružnice prelazi u standardni. Iz standardnog oblika znamo odrediti koordinate središta i polumjer.

00:00

$S (- 2, 1), r = 3 \sqrt{2}$ $S (- 2, 1), r = 3 \sqrt{2}$

Zadatak 1.

Iz grafičkog prikaza odredite opći oblik jednadžbe kružnice.

S (2, - 3), T (0, 0)

$S (2, - 3), T (0, 0)$ i

r = \sqrt{{(0 - 2)}^{2} + {(0 + 3)}^{2}} = \sqrt{13}

$r = \sqrt{{(0 - 2)}^{2} + {(0 + 3)}^{2}} = \sqrt{13}$

x^{2} + y^{2} - 4 x + 6 y = 0

$x^{2} + y^{2} - 4 x + 6 y = 0$

Poopćimo postupak prijelaza iz standardnog oblika u opći oblik jednadžbe kružnice.

Počnimo od poznate jednadžbe kružnice ${(x - p)}^{2} + {(y - q)}^{2} = r^{2}, S (p, q)$ ${(x - p)}^{2} + {(y - q)}^{2} = r^{2}, S (p, q)$ je središte i $r$ $r$ polumjer dane kružnice. Kvadriranjem i sređivanjem izraza dolazimo do opće jednadžbe kružnice $x^{2} + y^{2} + A x + B y + C = 0 .$ $x^{2} + y^{2} + A x + B y + C = 0 .$ Prikažimo realne koeficijente $A, B i C$ $A, B i C$ s pomoću poznatih koordinata središta i polumjera, $p, q i r .$ $p, q i r .$

Označite redoslijed koraka prijelaza iz jednog oblika jednadžbe kružnice u drugi.

$x^{2} + y^{2} - 2 p x - 2 q y + p^{2} + q^{2} = r^{2}$ $x^{2} + y^{2} - 2 p x - 2 q y + p^{2} + q^{2} = r^{2}$
$x^{2} + y^{2} - 2 p x - 2 q y + p^{2} + q^{2} - r^{2} = 0$ $x^{2} + y^{2} - 2 p x - 2 q y + p^{2} + q^{2} - r^{2} = 0$
$x^{2} - 2 p x + p^{2} + y^{2} - 2 q y + q^{2} = r^{2}$ $x^{2} - 2 p x + p^{2} + y^{2} - 2 q y + q^{2} = r^{2}$

null

Povežite koeficijente $A, B i C$ $A, B i C$ iz općeg oblika jednadžbe kružnice s dobivenim koeficijentima uz nepoznanice i sa slobodnim koeficijentom.

$B =$ $B =$	$- 2 p$ $- 2 p$
$C =$ $C =$	$- 2 q$ $- 2 q$
$A =$ $A =$	$p^{2} + q^{2} - r^{2}$ $p^{2} + q^{2} - r^{2}$

null

Čemu je jednak $r^{2} ?$ $r^{2} ?$

r^{2} = p^{2} + q^{2} + C

$r^{2} = p^{2} + q^{2} + C$

r^{2} = p^{2} + q^{2} - C

$r^{2} = p^{2} + q^{2} - C$

r^{2} = p^{2} + q^{2}

$r^{2} = p^{2} + q^{2}$

r^{2} = C - p^{2} + q^{2}

$r^{2} = C - p^{2} + q^{2}$

null

Zanimljivost

Za polumjer se često koristi riječ radijus (latinskog je podrijetla, od nje dolazi i oznaka $r$ ). Pojam se prvi put pojavljuje 1569. godine u Geometriji (djelo francuskog matematičara Ramusa), ali je opće prihvaćen tek u 17. stoljeću. U ovom kontekstu prvi put ga spominje Ciceron u često citiranoj rečenici: Krug je sastavljen od jednakih radijusa koji izlaze iz njegova središta.

Primjer 2.

Iz općeg oblika jednadžbe kružnice $x^{2} + y^{2} - 2 x = 4$ odredimo koordinate središta i polumjer.

Izjednačimo koeficijente s izrazima koje smo dobili kvadriranjem standardnog oblika jednadžbe kružnice.

$\begin{array}{r} - 2 p = - 2 & \Rightarrow p = 1 \\ - 2 q = 0 & \Rightarrow q = 0 \\ r^{2} = 1^{2} + 0 - (- 4) & \Rightarrow r^{2} = 5 \end{array}\}$ $S (1, 0), r = \sqrt{5}$

Na isti način riješte sljedeće zadatke.

Kolekcija zadataka #1

Odredite koordinate središta i polumjer kružnice $x^{2} + y^{2} - 8 x + 6 y + 23 = 0 .$

$S (4, - 3), r = \sqrt{2}$

Odredite koordinate središta i polumjer kružnice $x^{2} + y^{2} + 6 x - 2 y + 10 = 0 .$

Rješenje je jedna točka $S (- 3, 1), r = 0 .$

Odredite koordinate središta i polumjer kružnice $x^{2} + y^{2} - 10 x + 6 y + 36 = 0 .$

$S (5, - 3),$ ali zbog $r^{2} = 25 + 9 - 36 = - 2 < 0$ ne postoji tako zadana kružnica.

Skup točaka u ravnini opisan jednadžbom x²+y²+Ax+By+C=0

Vidjeli smo da nije baš svaki oblik $x^{2} + y^{2} + A x + B y + C = 0$ jednadžba kružnice.

Možete li odrediti uvjete kada je kružnica dobro zadana, odnosno kada postoji $r > 0 ?$

Iz linearnih koeficijenata pronađemo koordinate središta moguće kružnice te s pomoću sljedećih uvjeta provjerimo postoji li neprazan skup točaka opisan jednadžbom.

$p^{2} + q^{2} = C$	Skup opisan jednadžbom je prazan skup.
$p^{2} + q^{2} < C$	Skup opisan jednadžbom je točka.
$p^{2} + q^{2} > C$	Skup opisan jednadžbom je kružnica.

null

Koje jednadžbe opisuju skupove točaka različitih od praznog skupa?

$2 x^{2} + 2 y^{2} - 4 x + 8 y + 8 = 0$

$x^{2} + 2 y^{2} - 2 x - 4 y + 4 = 0$

$x^{2} + y^{2} - 6 x + 8 y + 25 = 0$

$x^{2} + y^{2} + 6 x + 8 y + 24 = 0$

$x^{2} + y^{2} + 6 x - 8 y + 26 = 0$

$2 x^{2} + y^{2} - 6 x - 8 y + 24 = 0$

null

...i na kraju

Zapamtimo!

Rješenje jednadžbe

$x^{2} + y^{2} + A x + B y + C = 0$ ovisi o tome postoji li realni broj

$r$ za koji vrijedi

$r^{2} = \frac{A^{2}}{4} + \frac{B^{2}}{4} - C.$

Uvjet	Skup točaka $(x, y)$ u ravnini opisan jednadžbom
$\frac{A^{2}}{4} + \frac{B^{2}}{4} > C$	kružnica $k (S (p, q), r)$
$\frac{A^{2}}{4} + \frac{B^{2}}{4} = C$	točka $S (p, q)$
$\frac{A^{2}}{4} + \frac{B^{2}}{4} < C$	prazan skup

Uvjet

Skup točaka

$(x, y)$ u ravnini opisan jednadžbom

$\frac{A^{2}}{4} + \frac{B^{2}}{4} > C$

kružnica

$k (S (p, q), r)$

$\frac{A^{2}}{4} + \frac{B^{2}}{4} = C$

točka

$S (p, q)$

$\frac{A^{2}}{4} + \frac{B^{2}}{4} < C$

prazan skup

Usavršite vještinu traženja središta i polumjera iz zadane jednadžbe kružnice s pomoću sljedeće interakcije. Rješenje prikažite grafički pomicanjem točke središta i točke na kružnici kojom određujete polumjer kružnice.

Na početku...

Opći oblik jednadžbe kružnice

Primjer 1.

Zadatak 1.

Zanimljivost

Primjer 2.

Kolekcija zadataka #1

Skup točaka u ravnini opisan jednadžbom x2+y2+Ax+By+C=0

...i na kraju

Skup točaka u ravnini opisan jednadžbom x²+y²+Ax+By+C=0