Matematika 4 - 6.6 Vjerojatnost događaja koji se ponavljaju

Na početku...

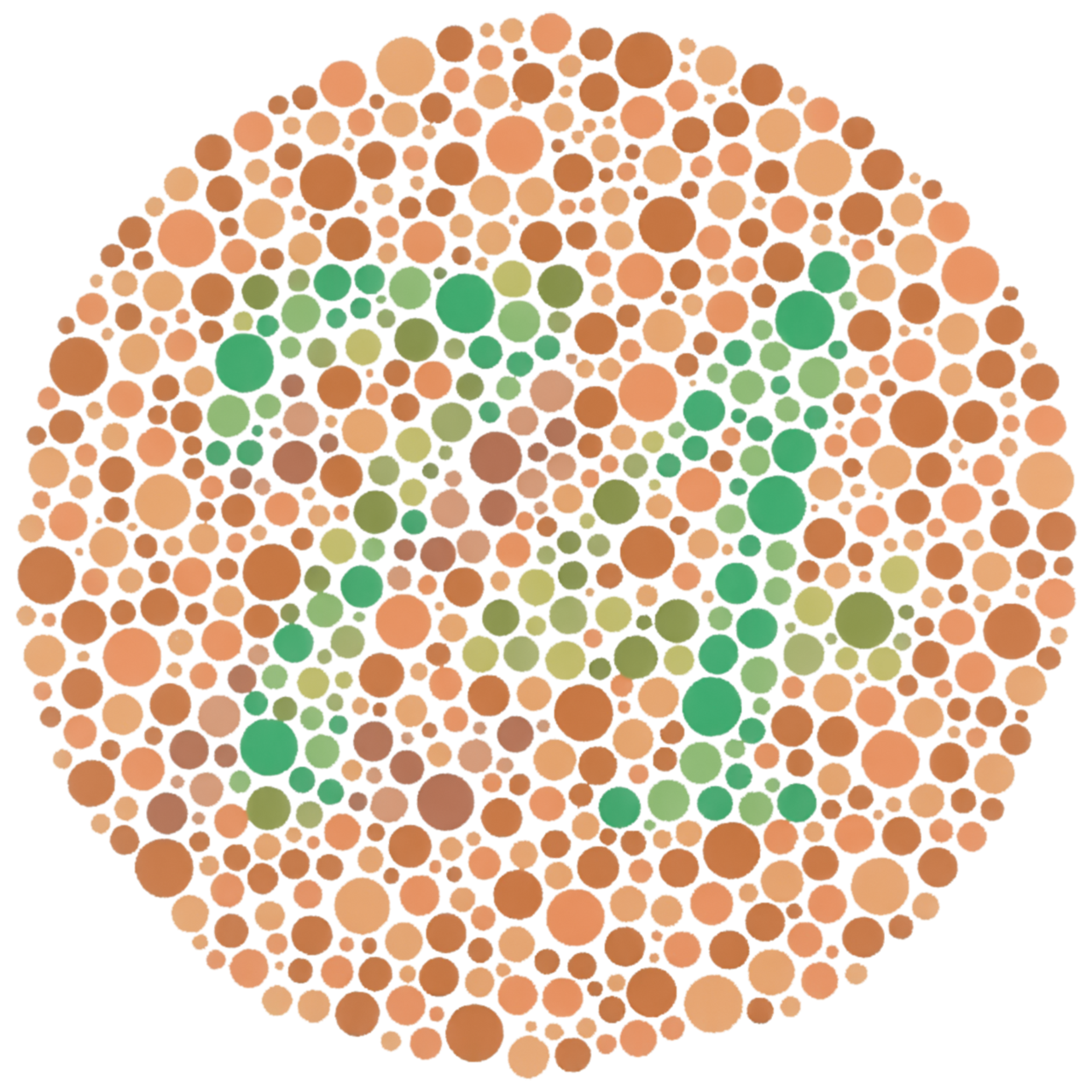
Fotografija prikazuje test za provjeru daltonizma — Test za daltonizam

U svijetu je $8 %$ muškaraca koji su daltonisti, odnosno imaju neki od poremećaja raspoznavanja boja. Kolika je vjerojatnost da će u skupini od $10$ muškaraca biti točno $3$ daltonista?

Istražimo

Kako ćemo izračunati traženu vjerojatnost?

Pokus se sastoji od provjere je li neki muškarac daltonist. Pokus ponavljamo $10$ puta. Stoga imamo niz od deset događaja koji mogu imati samo dva ishoda – daltonist ili nije daltonist. Ishod daltonist ćemo označiti s $1$ i obično zovemo uspjeh, a nije daltonist s $0$ ili neuspjeh. Povoljni su nizovi u kojima se pojavljuju točno tri jedinice, kao što je niz $1000001100 .$

Važno je napomenuti da rezultat testiranja za jednu osobu ne ovisi o rezultatima testiranja ostalih, pa se vjerojatnost jednog takva niza događaja računa kao vjerojatnost presjeka nezavisnih događaja:

$p (1000001100) = p (1) p (0) p (0) p (0) p (0) p (0) p (1) p (1) p (0) p (0) .$

Koliko je takvih nizova? Odgovorite na sljedeća pitanja vezano uz uvodni primjer.

Kolekcija zadataka #1

Vjerojatnost da je muškarac daltonist iznosi

Vjerojatnost da muškarac nije daltonist iznosi

null

Tada je vjerojatnost jednog povoljnog niza ishoda jednaka:

$\begin{array}{l} p (1000001100) = 0.08 \cdot 0.92 \cdot 0.92 \cdot 0.92 \cdot 0.92 \cdot 0.92 \cdot 0.08 \cdot 0.08 \cdot 0.92 \cdot 0.92 = {0.08}^{3} \cdot {0.92}^{7} \end{array} .$

null

Takvih nizova od tri jedinice i sedam nula, ima ukupno

2^{3}

(\begin{array}{l} 10 \\ 3 \end{array})

10 \cdot 9 \cdot 8 .

Pomoć:

Biramo tri mjesta u nizu gdje će biti jedinice.

null

Vjerojatnost svakog od povoljnih nizova ishoda računa se na isti način, a ukupnu vjerojatnost dobijemo zbrajanjem, prema formuli za vjerojatnost

disjunktnih

događaja.

null

Konačno, vjerojatnost da od 10 muškaraca točno tri budu daltonisti iznosi

\begin{array}{l} p (točno tri daltonista) = (\begin{array}{l} 10 \\ 3 \end{array}) \cdot {0.08}^{7} \cdot {0.92}^{3} \end{array} = 1.96 \cdot 10^{- 6}

\begin{array}{l} p (točno tri daltonista) = (\begin{array}{l} 10 \\ 3 \end{array}) \cdot {0.08}^{3} \cdot {0.92}^{7} \approx 0.034 \end{array}

null

Primjer 1.

Bacamo simetričnu kocku osam puta. Odredimo vjerojatnost da se šestica pojavi

točno 6 puta

barem 6 puta

barem jednom.

Pokus se ponavlja osam puta. Stoga imamo niz od osam događaja koji mogu imati samo dva ishoda, pala je šestica (uspjeh) ili nije pala šestica (neuspjeh). U jednom bacanju kocke vjerojatnost da padne šestica iznosi $\frac{1}{6},$ a da ne padne šestica je $1 - \frac{1}{6} = \frac{5}{6} .$ Tada je:
$\begin{array}{l} p (točno 6 puta šestica) = (\begin{array}{l} 8 \\ 6 \end{array}) {(\frac{1}{6})}^{6} {(\frac{5}{6})}^{2} \approx 0.000417 \end{array} .$
Barem šest puta broj $6,$ znači točno šest puta broj $6$ ili točno sedam puta broj $6$ ili točno osam puta broj $6 .$ Tada je:
$\begin{array}{l} p (barem 6 puta šestica) = (\begin{array}{l} 8 \\ 6 \end{array}) {(\frac{1}{6})}^{6} {(\frac{5}{6})}^{2} + (\begin{array}{l} 8 \\ 7 \end{array}) {(\frac{1}{6})}^{7} {(\frac{5}{6})}^{1} + (\begin{array}{l} 8 \\ 8 \end{array}) {(\frac{1}{6})}^{8} \approx 0.00044 \end{array}$
Barem jednom broj $6$ jednostavnije računamo kao:
$\begin{array}{l} p (barem jedna šestica) = 1 - p (niti jedna šestica) = 1 - {(\frac{5}{6})}^{8} \approx 0.767 \end{array} .$

Na osnovi ovih primjera možemo poopćiti računanje vjerojatnosti događaja pri ponavljanju pokusa.

Ponavljamo neki pokus $n$ puta uzastopce u istim uvjetima. Pokus ima samo dva ishoda – uspjeh i neuspjeh. Ako je vjerojatnost uspjeha pri jednom izvođenju pokusa jednaka $p,$ a vjerojatnost neuspjeha $1 - p,$ tada je vjerojatnost da se uspjeh pojavi točno $k$ puta jednaka

$\begin{array}{l} p (točno k puta uspjeh) = (\begin{array}{l} n \\ k \end{array}) p^{k} {(1 - p)}^{n - k}, k \in \{0, 1, 2, . . ., n\} \end{array} .$

Ovaj se način računanja vjerojatnosti zove još i Bernoullijeva shema. Dokaz se provodi kao i u rješenju uvodnog primjera.

Zadatak 1.

Pri kontroli ispravnosti proizvoda u tvornici ustanovljeno je da s jedne proizvodne linije dolazi $16 %$ proizvoda s greškom. Proizvod se distribuira u kutijama koje sadrže $20$ komada tog proizvoda.

Izračunajte sljedeće vjerojatnosti.

Vjerojatnost da će u kutiji biti točno dva proizvoda s greškom iznosi

\approx 0.211 .

Vjerojatnost da je u kutiji najviše jedan proizvod s greškom iznosi

+

\approx 0.147 .

Vjerojatnost da je u kutiji barem jedan proizvod s greškom iznosi

\approx 0.969 .

(\begin{array}{l} 20 \\ 1 \end{array}) \cdot 0.16 \cdot {0.84}^{19}

{0.84}^{20}

(\begin{array}{l} 20 \\ 2 \end{array}) \cdot {0.16}^{2} \cdot {0.84}^{18}

1 - {0.84}^{20}

null

Zadatak 2.

U kutiji se nalazi $6$ bijelih i $9$ crnih kuglica. Na slučajni način vadimo jednu kuglicu, zapišemo boju i vratimo je natrag u kutiju. Ponavljamo taj pokus pet puta.

Odredite vjerojatnost da smo bijelu kuglicu izvukli najmanje četiri puta.
Odredite vjerojatnost da smo crnu kuglicu izvukli najviše dva puta.

Vjerojatnost da izvučemo bijelu ( $B$ ) odnosno crnu kuglicu ( $C$ ) pri jednom bacanju je $p (B) = \frac{2}{5},$ $p (C) = \frac{3}{5} .$

$\begin{array}{l} p (B najmanje 4 puta) = (\begin{array}{l} 5 \\ 4 \end{array}) {(\frac{2}{5})}^{4} {(\frac{3}{5})}^{1} + {(\frac{2}{5})}^{5} = 0.08704 \end{array}$

$\begin{array}{l} p (C najviše 2 puta) = (\begin{array}{l} 5 \\ 0 \end{array}) {(\frac{3}{5})}^{0} {(\frac{2}{5})}^{5} + (\begin{array}{l} 5 \\ 1 \end{array}) {(\frac{3}{5})}^{1} {(\frac{2}{5})}^{4} + (\begin{array}{l} 5 \\ 2 \end{array}) {(\frac{3}{5})}^{2} {(\frac{2}{5})}^{3} = 0.31744 \end{array} .$

Neki se pokus ponavlja $100$ puta, a vjerojatnost da se pri jednom izvođenju dogodio događaj $A$ iznosi $p$ $.$

Vjerojatnost da se nije dogodio događaj

A

pri jednom izvođenju tog pokusa iznosi

Vjerojatnost da se događaj

A

bar jednom dogodio iznosi

- {(1 - p)}^{100} .

null

Pokus se sastoji od bacanja simetrične kocke $10$ puta. Vjerojatnost da se točno $6$ puta pojavi broj manji od $5$ je

\approx 0.1123

\approx 0.2276

\approx 0.3345

\approx 0.4456 .

null

Pero pogađa metu s vjerojatnošću od $0.85 .$ U što se više Peri isplati kladiti s prijateljem, da će u $15$ gađanja metu pogoditi barem $12$ puta ili da će je u $12$ gađanja pogoditi barem $10$ puta ili da će je u $8$ gađanja pogoditi barem $7$ puta? Zapišite u poretku od najmanje do najviše isplativog.

u $8$ gađanja barem $7$ pogodaka
u $15$ gađanja barem $12$ pogodaka .
u $12$ gađanja barem $10$ pogodaka

Pomoć:

$p (bar 7) \approx 0.6571,$ $p (bar 10) \approx 0.7358,$ $p (bar 12) \approx 0.8226$

null

U školskoj kantini za desert poslužuju palačinke u tri od pet dana. Ako Ana ovaj mjesec ruča u kantini 10 dana, vjerojatnost da će jesti palačinke za desert

a. točno 7 puta je

.
b. najviše 3 puta je

.
c. bar 7 puta je

\approx 0.3823

\approx 0.215

\approx 0.0548

null

Koliko najmanje puta treba baciti dvije kocke pa da vjerojatnost događaja

\{zbroj 8 pojavio se bar jednom\}

bude najmanje

0.6 ?

Pomoć:

Riješite nejednadžbu $1 - {(\frac{31}{36})}^{n} > 0.6 .$

Postupak:

$n \geq 6.1277 \Rightarrow n = 7 .$

$p (5), p (6)$	$\approx 0.156$
$p (8)$	$\approx 0.273$
$p (7)$	$\approx 0.039$

6.6 Vjerojatnost događaja koji se ponavljaju

Na početku...

Istražimo

Kolekcija zadataka #1

Primjer 1.

Zadatak 1.

Zadatak 2.

Tko će pobijediti?

Zadatak 3.

Kolekcija zadataka #2

Isplati li se?

Zadatak 4.

Kolekcija zadataka #3

Primjer 2.

Kutak za znatiželjne

Zadatak 5.

...i na kraju

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: