Matematika 1 - 4.1 Rješavanje linearnih jednadžbi

Na početku...

Dječak i djevojčica igraju igru Zamislila sam broj.

Kako bismo zapisati taj problem?

Ako zamišljeni broj označimo kao nepoznanicu $x,$ tada prema problemu možemo zapisati algebarski izraz. Nepoznanica pomnožena s $4$ je $4 x .$ Tomu dodamo $3$ pa je $4 x + 3$ jednako $31 .$

Zapisujemo jednakost $4 x + 3 = 31 .$

Dobili smo linearnu jednadžbu.

Dobivenu jednadžbu treba riješiti. Što znači riješiti jednadžbu?

Riješiti jednadžbu znači odrediti sve realnoga broja $x$ koje uvrštene u umjesto $x$ daju njezine lijeve i desne strane.

null

Svaka takva vrijednost $x$ naziva se rješenje jednadžbe.

Primjer 1.

Jednadžbu $4 x + 3 = 31$ riješimo s pomoću vaganja.

Jednadžbu zamislimo kao vagu koja ima lijevu i desnu stranu, a jednakost znači da su obje strane vage u ravnoteži.

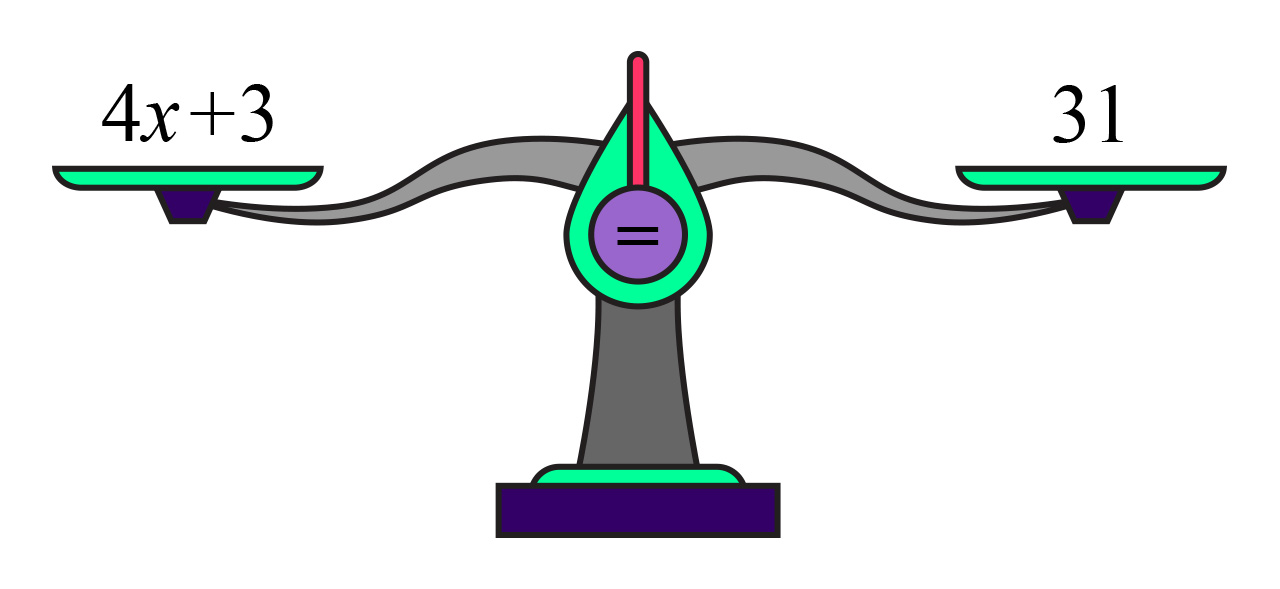
Ako od obiju strana oduzmemo broj $3,$ vaga će i dalje biti u ravnoteži.

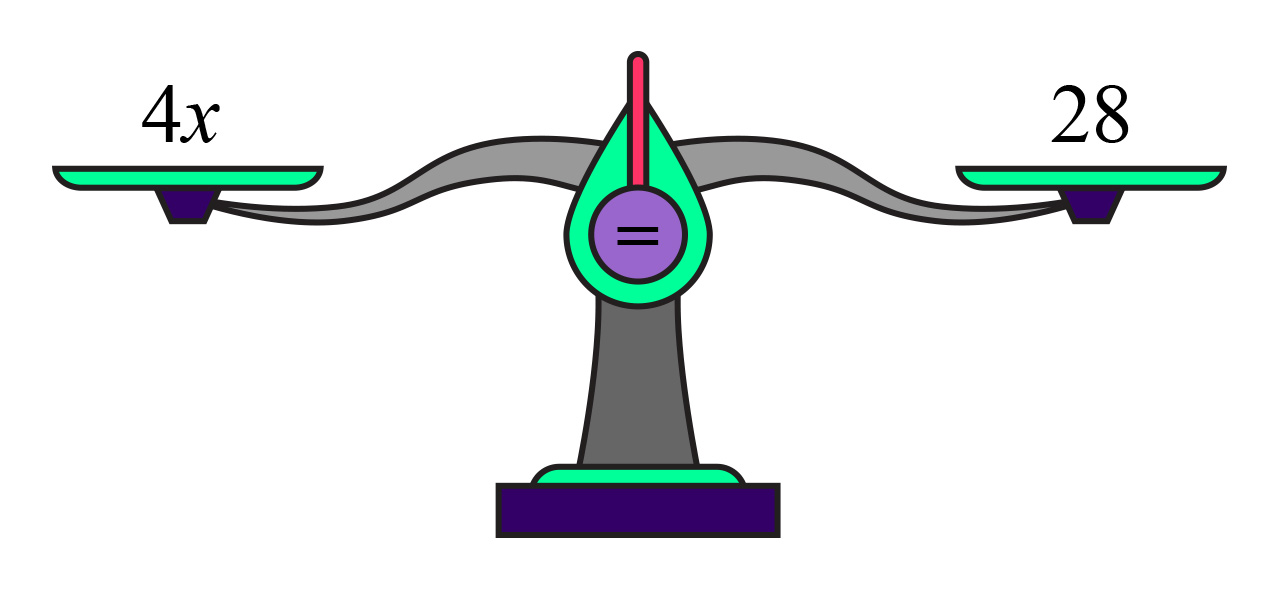
Ako obje strane podijelimo s $4,$ vaga će i dalje biti u ravnoteži.

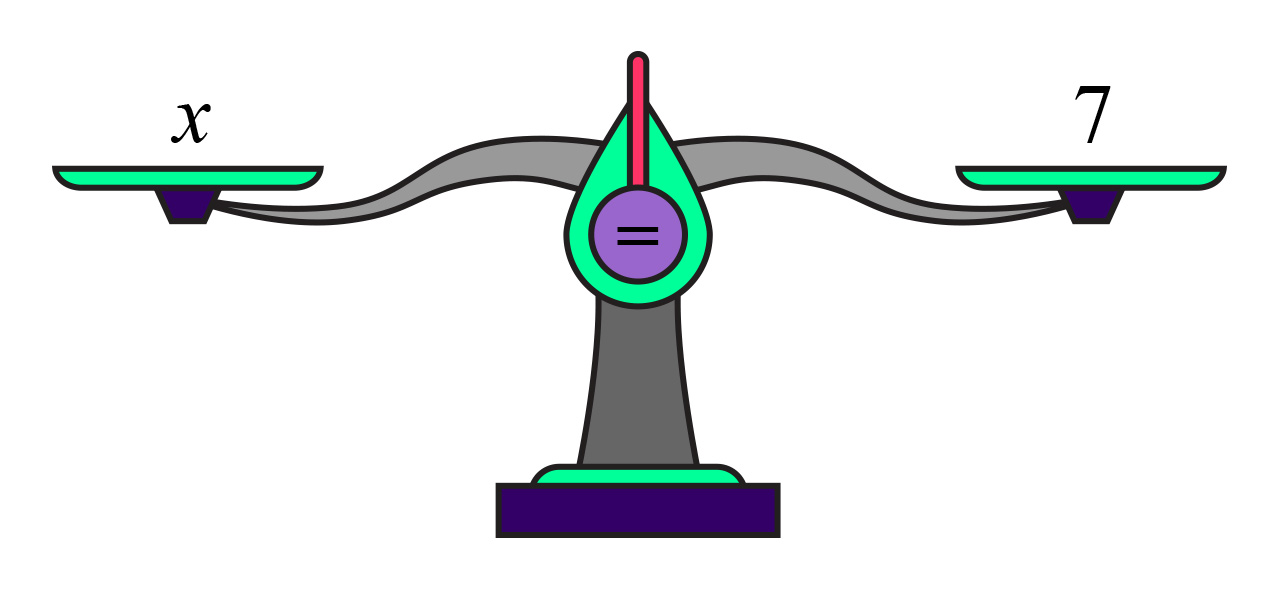
Odavde očitamo rješenje jednadžbe $x = 7 .$

U svakom je provedenom koraku vaga bila u ravnoteži, odnosno vrijedila je jednakost.

Što možemo reći za jednadžbe $4 x + 3 = 31$ i $4 x = 28 ?$

One imaju isto rješenje, $x = 7 .$

Jednadžbe koje imaju jednake skupove rješenja nazivaju se ekvivalentne jednadžbe.

Znači da smo raznim transformacijama početnu jednadžbu preoblikovali u ekvivalentne jednadžbe.

Što sve smijemo raditi s jednadžbama da dobijemo ekvivalentne jednadžbe?

T1: Ako objema stranama jednadžbe

ili oduzmemo

broj, dobit ćemo

jednadžbu.

isti

ekvivalentnu

dodamo

null

null
T2: Ako obje strane jednadžbe

ili podijelimo s

brojem

od nule, dobit ćemo

jednadžbu.

pomnožimo

različitim

istim

ekvivalentnu

null

null

Zadatak 1.

Gornje tvrdnje zapišite u bilježnicu simbolima.

T1: $a = b \Rightarrow a + c = b + c, a, b, c \in R$

T2: $a = b \Rightarrow a \cdot c = b \cdot c, a, b, c \in R, c≠ 0$

Pri rješavanju jednadžbe kažemo da smo broj ili izraz dodali ili oduzeli od obiju strana jednakosti. Na primjer, broj 3 smo oduzeli od obiju strana jednakosti.

$4 x + 3 = 31 / - 3$

$4 x + 3 - 3 = 31 - 3$ ili $4 x = 31 - 3$

Kraće možemo reći da smo broj 3 "prebacili" na drugu stranu pri čemu smo mu promijenili predznak. Zapis desno isti je korak proveden s pomoću prebacivanja broja $3$ sa suprotnim predznakom.

Zadatak 2.

Riješite linearne jednadžbe.

$11 x - 14 = 8, x =$

null

null
$17 - 5 x = 2, x =$

null

null
$3 x + 7 = 5 x - 17, x =$

null

null
$6 x + 13 = 7 - 2 x, x =$ .

null

null

Primjer 2.

Za koju će vrijednost realnoga broja $a$ rješenje linearne jednadžbe $5 x + 2 a - 7 = 1 - 3 x$ biti jednako $12 ?$

Prisjetimo se, što znači da je neki broj rješenje jednadžbe?

Kada taj broj uvrstimo umjesto nepoznanice, trebamo dobiti istinitu jednakost, odnosno

$5 \cdot 12 + 2 a - 7 = 1 - 3 \cdot 12.$

Dobili smo jednadžbu s nepoznanicom $a .$ Riješimo je.

$60 + 2 a - 7 = 1 - 36$

$2 a = - 88$

$a = - 44$

Dakle, kad je $a = - 44,$ tada će zadana jednadžba imati rješenje $x = 12 .$

Provjerite!

Zadatak 3.

Za koju će vrijednost realnog broja $t$ rješenje linearne jednadžbe $\frac{x}{3} + 11 = t x + 8$ biti jednako $- 4 ?$

$t = - \frac{5}{12}$

Jednadžbe koje se svode na linearne jednadžbe

Neke nam jednadžbe isprva izgledaju složeno, ali ih jednostavnim računskim radnjama možemo svesti na linearne jednadžbe.

Za jednadžbe u kojima je nepoznanica u nazivniku treba nakon rješavanja provjeriti prihvaćamo li rješenje ili ne.

Primjer 4.

Riješimo jednadžbu $\frac{x + 2}{x^{2} - 4} = 0 .$

Ta se jednadžba također svodi na linearnu jednadžbu jer znamo da je razlomak jednak nula ako mu je brojnik jednak nuli. To znači

$x + 2 = 0,$ odnosno

$x = - 2 .$

Međutim, ako taj broj uvrstimo u nazivnik, vrijednost će nazivnika biti nula pa taj broj ne može biti rješenje jednadžbe, to jest kažemo da zadana jednadžba nema rješenja.

Uparite jednadžbu s pripadajućim rješenjem.

$\frac{2 x - 5}{x - 2} = 5$	$- 1$
$5 + \frac{3}{x} = 2$	$\frac{5}{3}$
$\frac{3}{2 x} + \frac{1}{x} = 4 - \frac{5}{3 x}$	$\frac{25}{24}$
$20 - \frac{x}{2 x - 1} = 4$	$\frac{16}{31}$

null

U sljedećim zadatcima primjenjujemo distributivnost i formule za kvadrat binoma te razliku kvadrata.

Zadatak 7.

Riješite jednadžbe.

$(x - 1) (x + 3) + 7 = {(x - 2)}^{2}$
$(2 x - 5) (2 x + 5) = (4 x - 9) (x + 3)$
$11 - {(x - 4)}^{2} = (1 - x) (11 + x)$
${(\frac{3}{4} x + \frac{1}{5})}^{2} + (1 - \frac{3}{4} x) (1 + \frac{3}{4} x) = \frac{1}{2}$

$x = 0$
$x = \frac{2}{3}$
$x = \frac{8}{9}$
$x = - 1.8$

Primjer 5.

Riješimo jednadžbu $(x - 4) (x + 7) = 0 .$

Iako je dana jednadžba drugog stupnja, tako faktorizirana omogućuje nam da je jednostavno riješimo. Uočimo da je zadan umnožak dvaju izraza koji mora biti jednak nuli.

Umnožak dvaju brojeva ili izraza

A \cdot B

jednak je nuli ako je

barem jedan

od brojeva ili izraza

A

ili

B

jednak nuli.
To zapisujemo:

A \cdot B = 0 \Leftrightarrow A = 0

ili

B = 0 .

null

To znači da je

$(x - 4) (x + 7) = 0$

ako je

$x - 4 = 0$ ili $x + 7 = 0,$

odnosno

$x = 4$ ili $x = - 7 .$

Svakoj jednadžbi pridružite odgovarajuća rješenja.

- 1

6

\frac{3}{2}

7

- \frac{1}{2}

1

- \frac{7}{2}

$(2 x + 7) (x + 1) = 0$

$x^{2} - 3 x + \frac{9}{4} = 0$

$x^{2} - 7 x + 6 = 0$

$2 x^{2} - 13 x - 7 = 0$

null

Kutak za znatiželjne

U ovisnosti o realnom parametru $p$ raspravite rješenja linearnih jednadžbi:

$1 - 3 p + 5 x = p x - 2 p + 6 x$
$p^{2} (x + 2) = p x + 2$
$\frac{3 x - 1}{p + 3} + \frac{x - 2}{p^{2} + 3 p} = \frac{5}{p}$
$\frac{4 x - 1}{p - 2} - \frac{2 x + 7}{p + 2} = \frac{10}{p^{2} - 4} .$

Izrazite nepoznanicu $x$ pa provjerite za koje vrijednosti parametra $p$ nije definirana.

za $p = - 1$ jednadžba nema rješenja, a za $p \neq - 1$ rješenje je $x = \frac{1 - p}{1 + p}$
za $p = 0$ jednadžba nema rješenja, za $p = 1$ rješenje je bilo koji realni broj, a za $p \neq 0$

i $p \neq 1$ rješenje je $x = \frac{- 2 (1 + p)}{p}$
za $p = 0$ ili $p = - 3$ ili $p = - \frac{1}{3}$ jednadžba nema rješenja, za $p \neq 0$ i $p \neq - 3$ i $p \neq - \frac{1}{3}$ rješenje je $x = \frac{17 + 6 p}{3 p + 1}$
za $p = 2$ ili $p = - 2$ ili $p = - 6$ jednadžba nema rješenja, za $p \neq 2$ i $p \neq - 2$ i $p \neq - 6$ rješenje je $x = \frac{4 p - 1}{p + 6}$

Kolekcija zadataka 1

Zadatak 8.

Prevedite rečenice u linearne jednažbe i riješite ih.

Ako od nekoga broja oduzmemo $7,$ rezultat je $15 .$ Koji je to broj?
Ako neki broj pomnožimo sa $6,$ a dobiveni umnožak umanjimo za $3,$ rezultat je $69 .$ Koji je to broj?
Ako trokratnik nekoga broja oduzmemo od $85,$ rezultat je $13 .$ Koji je to broj?
Ako nekomu broju dodamo $37$ i rezultat udvostručimo, dobit ćemo $104 .$ Koji je to broj?

$x - 7 = 15 \Rightarrow x = 22$
$6 x - 3 = 69 \Rightarrow x = 12$
$85 - 3 x = 13 \Rightarrow x = 24$
$(x + 37) \cdot 2 = 104 \Rightarrow x = 15$

Zadatak 9.

Uparite redni broj zadatka s odgovarajućom jednadžbom i riješite ju.

U razredu je $29$ učenika. Djevojaka je za $5$ više nego dječaka. Koliko je djevojaka u razredu?
Hana je trostruko mlađa od svoje sestre. Za $5$ godina bit će dvostruko mlađa. Koliko godina ima Hana?
Duljina pravokutnika je za $5 cm$ veća od širine. Ako je opseg pravokutnika $29 cm,$ koliko iznosi širina?
Ako neki broj pomnožimo s $4$ i oduzmemo $29,$ dobit ćemo broj koji je za $5$ veći od dvostrukoga broja. Koji je to broj?

b.	$4 x - 29 = 2 x + 5$
d.	$3 x + 5 = 2 (x + 5)$
a.	$x + (x + 5) = 29$
c.	$2 [x + (x + 5)] = 29$

null

a. U razredu je djevojaka.

null

b. Hana ima godina.

null

c. To je broj .

null

d. Širina pravokutnika iznosi

cm .

null

Zatvori

4.1 Rješavanje linearnih jednadžbi

Na početku...

Zadatak 1.

Zadatak 2.

Zadatak 3.

Broj rješenja linearne jednadžbe

Zadatak 4.

Zadatak 5.

Jedno rješenje

Nema rješenja

Beskonačno mnogo rješenja

Zadatak 6.

Jednadžbe koje se svode na linearne jednadžbe

Zadatak 7.

$(2 x + 7) (x + 1) = 0$

$x^{2} - 3 x + \frac{9}{4} = 0$

$x^{2} - 7 x + 6 = 0$

$2 x^{2} - 13 x - 7 = 0$

Kutak za znatiželjne

Kolekcija zadataka 1

Zadatak 8.

Zadatak 9.

...i na kraju

4.2 Jednadžbe s apsolutnim vrijednostima

Na početku...

Zadatak 1.

Zadatak 2.

Zadatak 3.

Broj rješenja linearne jednadžbe

Zadatak 4.

Zadatak 5.

Jedno rješenje

Nema rješenja

Beskonačno mnogo rješenja

Zadatak 6.

Jednadžbe koje se svode na linearne jednadžbe

Zadatak 7.

2 x + 7 x + 1 = 0

x 2 - 3 x + 9 4 = 0 ​

x 2 - 7 x + 6 = 0

2 x 2 - 13 x - 7 = 0 ​

Kutak za znatiželjne

Kolekcija zadataka 1

Zadatak 8.

Zadatak 9.

...i na kraju

4.2 Jednadžbe s apsolutnim vrijednostima

$(2 x + 7) (x + 1) = 0$

$x^{2} - 3 x + \frac{9}{4} = 0$

$x^{2} - 7 x + 6 = 0$

$2 x^{2} - 13 x - 7 = 0$