


Osnovne pojmove u geometriji prostora čine tri vrste objekata (skupova točaka). To su točke, pravci i ravnine. Njih ne definiramo, nego ih opisujemo osnovnim geometrijskim tvrdnjama ili aksiomima s kojima ste se upoznali u jedinici 8.1 Abeceda stereometrije. Naučili ste i u kojem međusobnom odnosu mogu biti točke, pravci i ravnine u prostoru. Koristeći se analogijom, neka svojstva i preslikavanja ravnina poopćili smo u prostoru. Zrcalna, osna i centralna simetrija izometrična su preslikavanja prostora. (Kada je preslikavanje izometrija?) Znamo da postoji preslikavanje koje mijenja udaljenosti između točaka. Takvo preslikavanje nazivamo homotetija. Pomoću definicija konveksnosti skupova točaka uveli smo pojmove konveksnog, odnosno pravilnog poliedra.
Gdje je u cijeloj toj priči ova slika nemogućeg trokuta? Naše trodimenzionalno viđenje stvari ponekad prijeđe granice realnog. Imali ste zasigurno priliku već vidjeti neke crteže na papiru koji su izgledali stvarno. Međutim, pažljivijim promatranjem i praćenjem nacrtanih linija primjećujemo da su u trodimenzionalnom svijetu ti oblici zapravo nemogući, kao i ovaj trokut na slici. Radi se o perceptivnim varkama. Više o perceptivnim varkama pročitajte u Matematičkom panoptikumu časopisa MiŠ (12/2001.).

Maurits Cornelis Escher (1898.-1972.), nizozemski slikar i grafičar. Poznat je po svojim bakropisima i drvorezima. Oslikavao je realno nemoguće konstrukcije. Najpoznatija njegova litografija jest Slap. U toj je litografiji iskoristio nemoguće trokute da bi kreirao pravi perpetuum mobile (lat. neprestano pokretljivo). Više o optičkim iluzijama i perceptivnim varkama pročitajte na portalu Optike te hrvatskom Wikiwandu.
U scenarijima poučavanja e-Škole potražite scenarij Nesavršenost zora. Priča počinje gledanjem poznatog animiranog filma Simpsoni, kao iskorakom u treću dimenziju, da bi na kraju završila u muzeju iluzija.
Pokušajte napraviti nemogući trokut iz uvoda.
Otkrijte više detalja o nevjerojatnom umjetniku Mauritsu Cornelisu Escheru. Nadahnut matematikom i koristeći se nesavršenošću zora, drvorezima i litografijama prikazao je maštovito zamišljene građevinske konstrukcije i trodimenzionalne prizore, izmišljene prostore, izvorne prikaze ideje perpetuum mobile i problema beskonačnosti. Pročitajte zanimljiv članak o M. C. Escheru na portalu Telegram.
Pogledajte razrađeni scenarij poučavanja Nesavršenost zora
s nizom dodatnih poveznica i videozapisa
na stranicama Zdravstvene škole Split koji vam može pomoći u podjeli i realizaciji poslova.
Napravite prezentaciju svojih radova.

Möbiusova traka je
(dvodimenzionalna)
ploha koja ima samo jednu stranu i jedan rub. Kada bismo na plohu npr. stavili mrava, obišao bi je cijelu (ne prelazeći preko ruba) i vratio bi se na početak u obliku svoje zrcalne slike (pretpostavimo da mrav ide kuda mi želimo). Pokušajte sami izraditi ovu traku ("papirni prsten sa zaokretom"). Za izradu vam je potreban komad papira pravokutnog oblika. Jedan kraj trake zakrenite za
i zalijepite krajeve. Više o izradi trake pročitajte u rubrici Zanimljiva matematika časopisa MiŠ (22/2003.). Traka ima svoju primjenu i u prirodnim i u društvenim znanostima. Traka je bila glavna tema Comenius projekta
Ins and outs of the magic Möbius trip
koji je XV. gimnazija iz Zagreba provela sa svojim partnerima iz Europe. Više o projektu koji vam može biti inspiracija za izradu i istraživanje primjene trake potražite u digitalnom časopisu Pogled kroz prozor.

August Ferdinand Möbius
(1790.-1868.), njemački matematičar i astronom. Pronašao je jednostavni primjer jednostrane plohe, Möbiusove plohe.
Istodobno, neovisno o njemu, na takvu je plohu uputio i Johann Benedict Listing (1808.-1882.), njemački matematičar i fizičar.
Tvorevina slična toj plohi jest i Kleinova boca, zatvorena jednostrana ploha koja prodire kroz samu sebe, neorijentirana površina bez granice. Dobila je ime po Felixu Kleinu (1849.-1925.), njemačkom matematičaru.
Nakon izrade Möbiusove trake, istražujući, odgovorite na postavljena pitanja.
Ako počnemo bojiti traku, ona će cijela biti obojena istom bojom, kao što ćemo, ako povlačimo crtu bez prekida, opet doći u početnu točku. Traka se rezanjem neće raspasti, nego će prijeći u užu dvostranu plohu.
Tetraedar (pravilna trostrana piramida) jedan je od pet pravilnih konveksnih poliedara. Proučimo ga detaljnije kao prostorni analogon trokuta.
Trokut je najmanji konveksni skup ravnine koji sadrži točke koje su . Tetraedar je najmanji konveksni skup prostora koji sadrži točke koje su .
Kako se zove dužina koja spaja vrh i polovište suprotne stranice trokuta?
Težišnica tetraedra dužina je koja spaja tetraedra i težište .
Težišnice se sijeku u težištu trokuta, odnosno tetraedra. Težište dijeli težišnicu
od vrha
trokuta u omjeru .
Težište dijeli težišnicu od vrha tetraedra u omjeru
.
Ponovimo odnose točaka, pravaca i ravnina u prostoru. Skicirajmo tetraedar
te mu odredimo težišta svih strana (kao u interaktivnom predlošku).
Koristite se interaktivnim predloškom kako biste grafički predočili pitanja u nastavku. S alatima ponuđenima u predlošku nacrtajte pravce i ravnine koji se traže u zadatku te odredite njihova sjecišta.
U kojem položaju su pravci
Neka su
redom težišta pripadajućih strana tetraedra
. Što se dobije kada se spoje dobivena težišta?
Jesu li točke
komplanarne?
U kojem se međusobnom položaju nalaze ravnine
U kojem se međusobnom položaju nalaze ravnine
U kojem se međusobnom položaju nalaze ravnine
U kojem se međusobnom položaju nalaze presjek ravnina
te pravac
U kojem se međusobnom položaju nalaze pravci
Jesu li točke
komplanarne?
U kojem se položaju nalazi pravac
u odnosu na ravninu

Tetraedar, osim što je kroz povijest bio značajan matematičarima i filozofima (od Platona koji ga povezuje s vatrom preko Keplera koji ga smješta u Sunčev sustav pa do danas), izuzetno je značajan i kemičarima. Tetraedarski je model ugljikova atoma, tj. "lijevi" i "desni" raspored četiriju različitih skupina oko središnjeg ugljikovog atoma. Na slici je molekula metana
bezbojnog plina. Vrhovi tetraedra predstavljaju atome vodika (svi spojeni na atom ugljika koji se nalazi u težištu tetraedra), a njihove kovalentne veze dio su težišnica tetraedra. Metan je najjednostavniji ugljikovodik. Kut između kovalentnih veza iznosi
Provjerite postoji li odstupanje od kuta pravilnog tetraedra.
Od nastavnika iz kemije saznajte više o takvim spojevima. Istražite što su to Platonovi ugljikovodici (molekularne reprezentacije pravilnih poliedara) i može li ih se naći u prirodi.

Neka je težište tetraedra Izračunajte kut pri vrhu trokuta (kao na slici).
Uočite trokut
Izračunajte njegov kut pri vrhu
pomoću definicije sinusa pravokutnog trokuta. Duljina stranice
dvije je trećine duljine težišnice (točka
je težište trokuta
). Težišnica je jednaka
Pogledajte još jedanput sliku prethodnog zadatka i odgovorite na sljedeća pitanja.
U kojoj ravnini određenoj s trima točkama leži kut
Koje su ravnine okomite na ravninu

Pronađite na internetu mreže pravilnih poliedara i u razredu napravite poliedre različitih veličina i oblika. Osim klasične izrade geometrijskih tijela, možete se iskušati u tehnici origamija. Proučite i pripremite materijale zajedno s predmetnim nastavnicima i napravite izložbu svojih radova u školi. Pogledajte kako to izgleda u jednoj učionici 2. razreda.
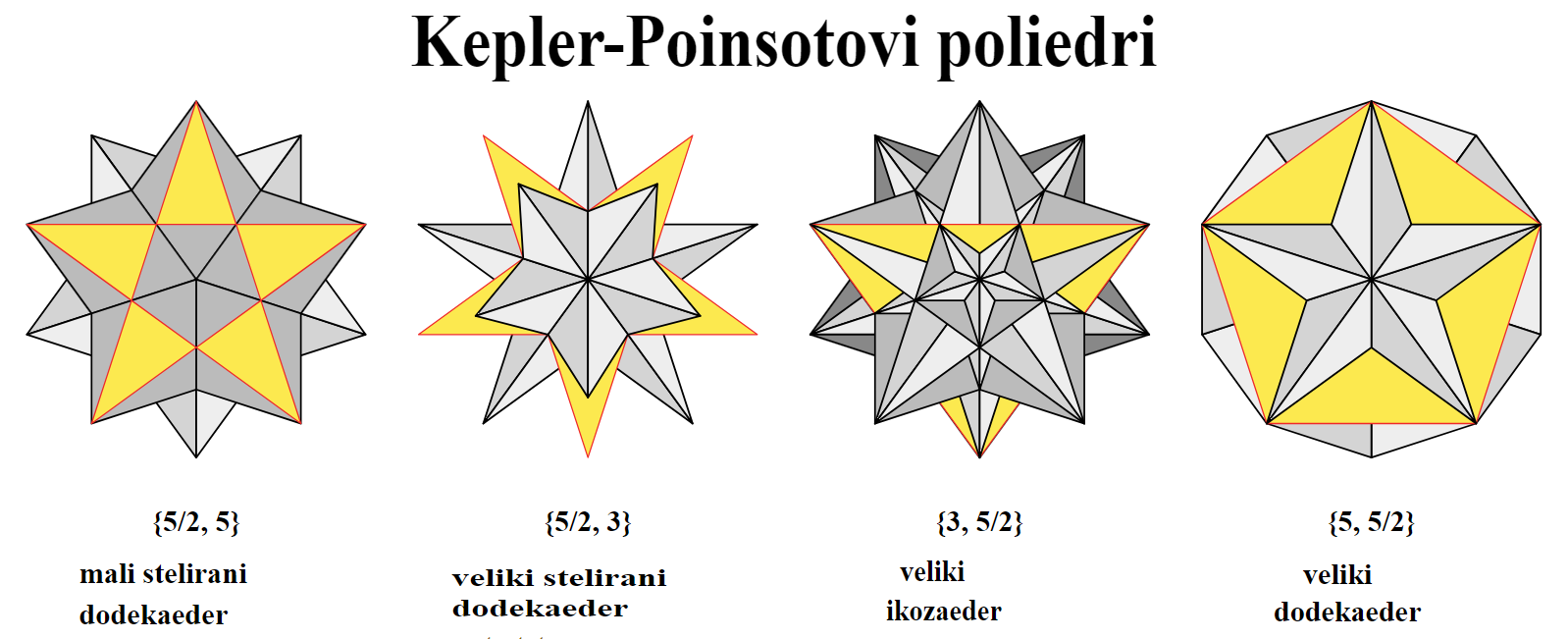
Nekoliko kratkih crtica o pravilnim poliedrima.
Upoznali smo se s temeljnim pojmovima prostora, vidjeli koliko smo usko povezani s tim pojmovima - što u znanosti, umjetnosti, filozofiji, geografiji i povijesti, a što u svakidašnjem životu. Geometrijska tijela i odnosi među njima nas okružuju, moramo ih samo prepoznati. Kada idete na izlet, u prirodu s razredom ili na putu od kuće do škole, osvrnite se oko sebe, uočite različite geometrijske oblike. Fotografirajte ih i pripremite za sljedeće module povezane s geometrijom prostora. Naučit ćemo računati obujmove tijela, njihove površine, odnose među njihovim veličinama te kako to primijeniti u svijetu koji nas okružuje. Tako ćete znati izračunati neke veličine za geometrijska tijela koja ste uočili promatrajući prirodu. Pogledajte što su, istražujući svijet, pronašli učenici Srednje škole Čazma.