

Pokušajte grafički predočiti što se zbiva s istosmjernim naponom i istosmjernom strujom tijekom vremena.
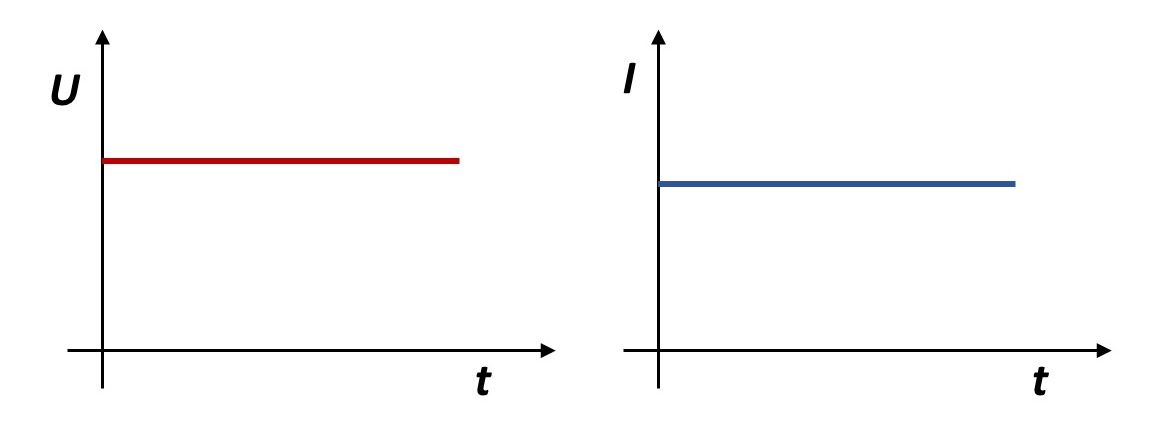
Istosmjerna struja ima uvijek isti smjer i u svakom trenutku jednaku jakost. Dijagrami ovisnosti struje o vremenu i napona o vremenu zorno prikazuju nepromjenjivost jakosti i smjera istosmjerne struje.
Pogledajmo u sljedećem pokusu kako izgleda napon naše gradske mreže.
Izmjeničnoj struji i naponu stalno se i u pravilnim vremenskim razmacima mijenjaju i smjer i iznos.
Promjenu iznosa i smjera izmjeničnog napona i izmjenične struje tijekom vremena zorno prikazuju sinusoide.
Vremenske ovisnosti napona gradske mreže i struje kroz neko trošilo mogu se prikazati periodičnim funkcijama:
gdje je
kružna frekvencija, a računa se kao
Frekvencija gradske mreže iznosi
Pritom su
trenutne vrijednosti izmjeničnih napona i struja, a
i
su maksimalne vrijednosti.
Izmjenična se struja stalno mijenja po vrijednosti i po smjeru, pa je njezina srednja vrijednost jednaka nuli.
Kod prolaska struje kroz otpornik omskog otpora ukupna se električna energija pretvara u toplinsku.
Toplinski se učinak izmjenične struje može usporediti s toplinskim učinkom istosmjerne struje tijekom prolaska kroz isti otpornik za isto vrijeme.
Efektivna vrijednost izmjenične struje jednaka je po veličini onoj stalnoj istosmjernoj struji
koja za isto vrijeme na jednakom otporniku razvija jednaku količinu topline Q.
Ako izmjenična struja efektivne jakosti
prolazi kroz vodič otpora R, toplinska je snaga:
Isti je izraz i za snagu istosmjerne struje jakosti
Kad se govori o naponu i jakosti izmjenične struje, smatra se da je riječ o efektivnim vrijednostima.
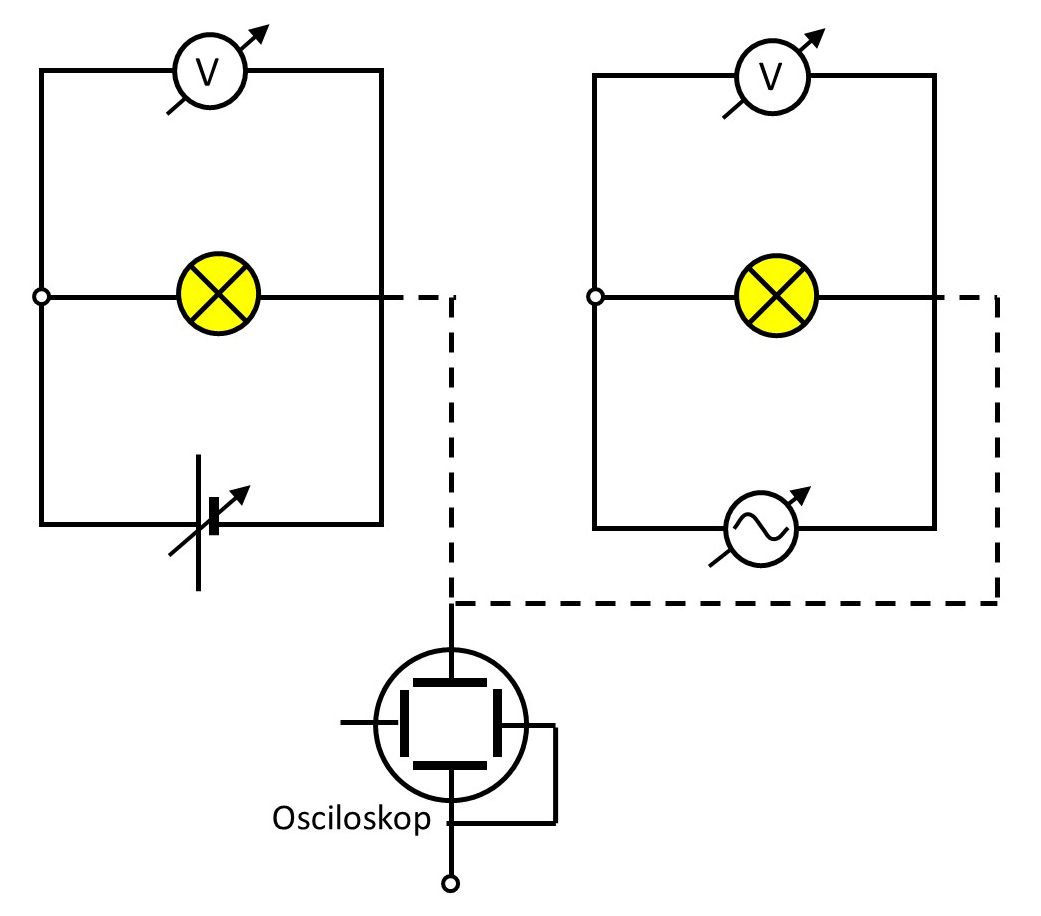
Pogledajte pokus u kojem se jedna od dviju istovjetnih žarulja spaja na istosmjerni izvor napona, a druga na izmjenični izvor napona. Razmatraju se efektivne vrijednosti izmjeničnog napona i struje.
Pri prolazu struje kroz trošilo snaga i rad proporcionalni su kvadratu jakosti struje pa je za toplinski učinak izmjenične struje bitna srednja vrijednost kvadrata jakosti struje. Zbog toga se u praksi upotrebljavaju efektivne vrijednosti napona i struje
Efektivna vrijednost izmjenične struje definira se kao vrijednost koju bi imala ona istosmjerna struja stalne jakosti koja bi u određenom vodiču proizvela jednaki toplinski učinak kao i ta izmjenična struja.
Veza između maksimalne i efektivne vrijednosti izmjenične struje i napona:
Efektivni je napon gradske mreže dok mu je maksimalna vrijednost
Efektivni napon i izmjenična struja
Efektivne vrijednosti napona i struje mogu se pojednostavnjeno odrediti na osnovi geometrijskih razmatranja.
Rad se električne struje može odrediti kao površina ispod
dijagrama na slici 1.
Trenutna se vrijednost snage na omskom otporniku kroz koji prolazi izmjenična struja može odrediti prema izrazu:
ili
Pri prolazu struje kroz trošilo snaga i rad proporcionalni su kvadratu jakosti struje pa je za toplinski učinak izmjenične struje bitna srednja vrijednost kvadrata jakosti struje.
Razmatramo srednju snagu izmjenične struje (slika 2).
Osjenčana je površina upravo jednaka površini ispod P, t dijagrama. Da su te površine jednake, možemo vidjeti i na osnovi površina osjenčanih u prikazu na slici 3.
U dijelu grafičkog prikaza ispod srednje vrijednosti upravo je toliko osjenčanih elemenata koliko ih je i iznad linije srednje vrijednosti.
Površina ispod grafa na slici 2 odgovara radu istosmjerne struje:
Rad izmjenične struje jednak je:
Uspoređujemo srednju snagu izmjenične struje sa snagom istosmjerne struje u vremenu jednog perioda:
Slijedi da je
Jakost struje efektivna je struja pa se veza između efektivnih i maksimalnih vrijednosti izmjenične struje zapisuje u obliku:
Analogno razmatranje vrijedi i za efektivne vrijednosti napona:
.
U strujnim krugovima mogu postojati:
Kada izmjenična struja prolazi kroz zavojnicu odnosno kondenzator, pojavljuje se induktivni odnosno kapacitivni otpor koji ovisi o induktivitetu
zavojnice odnosno o kapacitetu
kondenzatora kao i o frekvenciji
izmjenične struje.
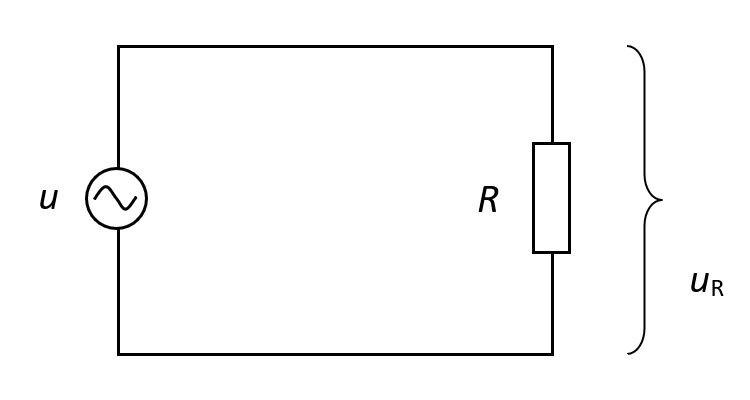
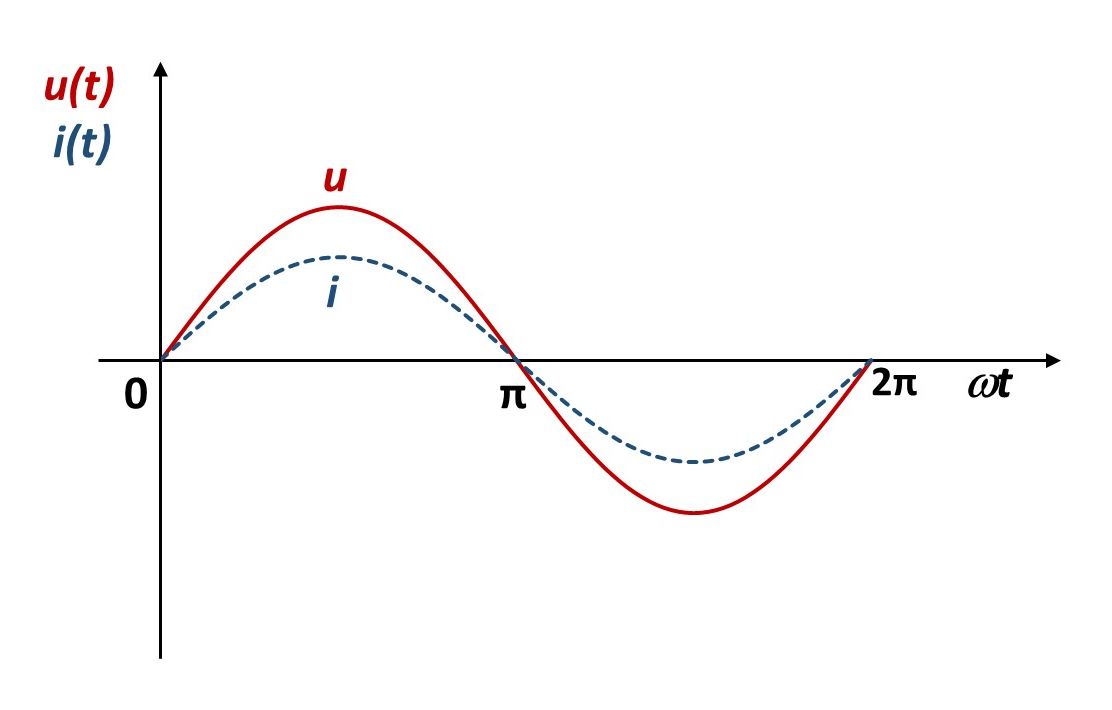
Ako je u krugu izmjenične struje trošilo omskog otpora , struja se u svakom trenutku može odrediti po Ohmovu zakonu:
Kako se napon i struja mijenjaju po istoj vremenskoj funkciji, struja i napon su u fazi, tj. fazni je pomak između njih nula, Ako se umjesto trenutnih vrijednosti uzimaju efektivne vrijednosti, Ohmov zakon poprima oblik (formalno kao za istosmjernu struju):
Pogledajte snimku animacije u kojoj su u
krug izmjenične struje
serijski spojeni otpornik i zavojnica. Očitavaju se naponi na zavojnici i struja u strujnom krugu. Što opažate? Jesu li struja i napon u fazi?
Izmjenični napon i struja nisu u fazi. Napon prethodi struji, tj. struja zaostaje za naponom. Fazni je pomak
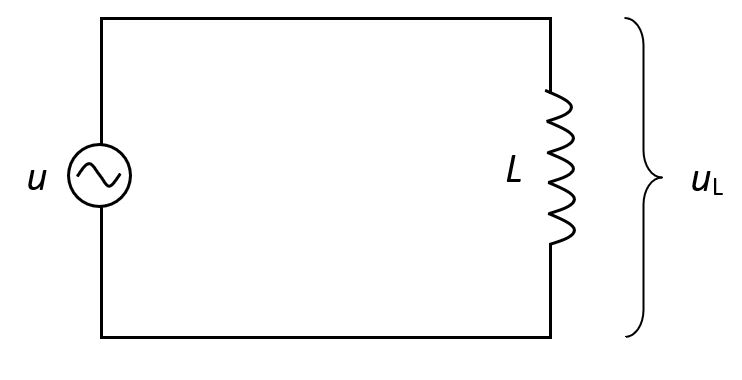
Na izvor izmjeničnog napona spojena je zavojnica induktiviteta i zanemarivoga omskog otpora. Zavojnica pruža prolasku struje određeni otpor. Taj je otpor uzrokovan samoindukcijom koja nastaje u zavojnici zbog stalne promjene izmjenične struje i naziva se induktivni otpor
Induktivni otpor proporcionalan je induktivitetu zavojnice i frekvenciji izmjenične struje:
tj.
Na slici je prikazana vremenska ovisnost struje i napona kada je zavojnica idealna (bez omskog otpora). Struja zaostaje za naponom jer se zavojnica zbog samoindukcije opire prolazu struje. Struja za naponom zaostaje za (tj. ).
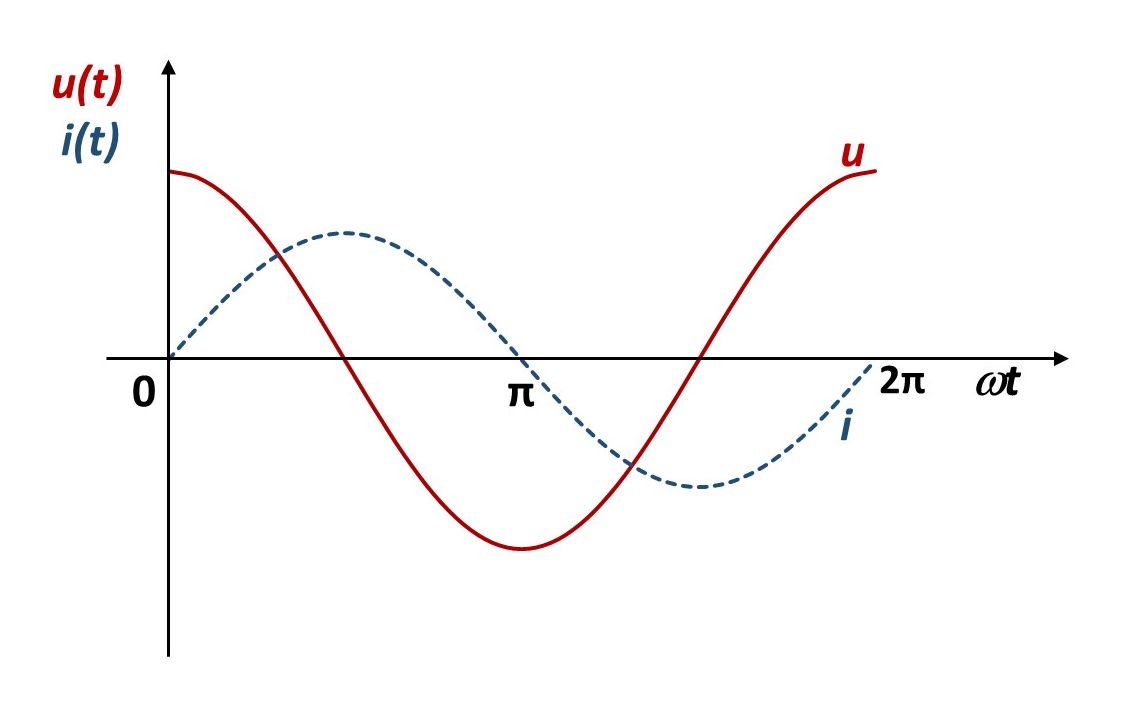
Induktivni je otpor jalovi otpor. On ne pretvara električnu energiju. U induktivnom se otporu električna energija pretvara u energiju magnetskog polja zavojnice.
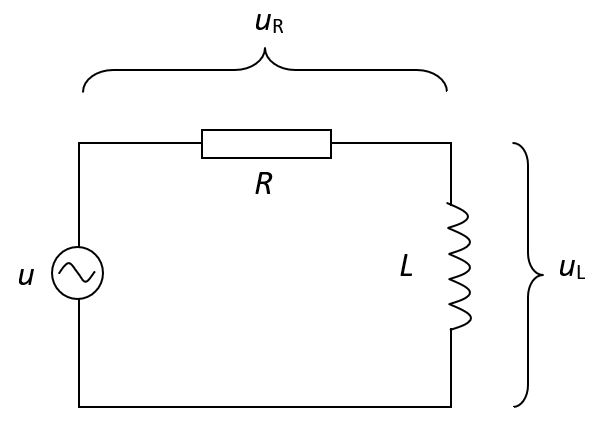
Realna zavojnica ima i određeni omski otpor koji je uzrokovan otporom žice namotaja. Razmotrimo slučaj kada se u strujnom krugu nalazi zavojnica induktivnog otpora i omskog otpora ili zavojnica i omski otpornik spojeni u seriju.
Ta se dva otpora ne mogu jednostavno algebarski zbrojiti jer struja kroz zavojnicu nije u fazi s naponom. Radni i reaktivni otpor zbrajaju se vektorski. Najjednostavniji je način nacrtati vektorski dijagram za napone ili za otpore.
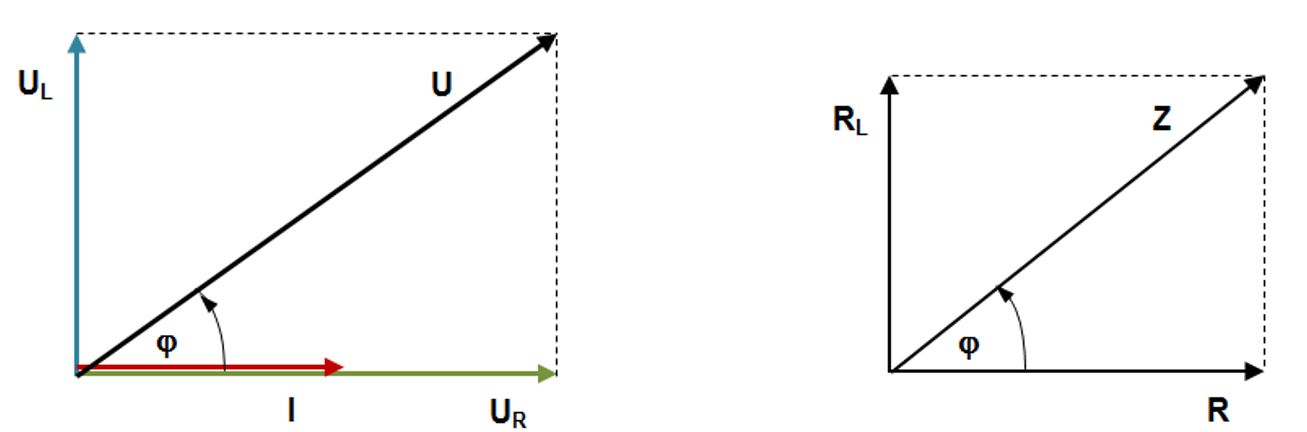
Ukupni napon je vektorski zbroj napona na induktivnom i radnom otporu:
Neka je ukupni otpor ili impedancija. Prema Ohmovu zakonu je Kako je
i slijedi:
odnosno
Umjesto vektorskog dijagrama za napone može se crtati vektorski dijagram za otpore, iz njega izračunati ukupni otpor i množenjem sa strujom dobiti ukupni napon. Dobiva se isti rezultat. Fazni pomak napona u odnosu prema struji može se grafički odrediti iz vektorskog dijagrama ili s pomoću trigonometrijskih funkcija:
Ako je u krugu izmjenične struje samo radni otpor:
tj.
Ako je u krugu izmjenične struje samo induktivni otpor:
Ako se u strujnom krugu uz induktivni otpor nalazi i omski, zaostajanje struje za naponom je između i ovisno o omjeru
Pogledajte snimku animacije u kojoj su u
krug izmjenične struje
serijski spojeni otpornik i kondenzator. Očitavaju se naponi na kondenzatoru i struje u strujnom krugu. Što sada opažate? Jesu li struja i napon u fazi?
Izmjenični napon i struja nisu u fazi. Napon zaostaje za strujom ili struja prethodi naponu. Fazni je pomak
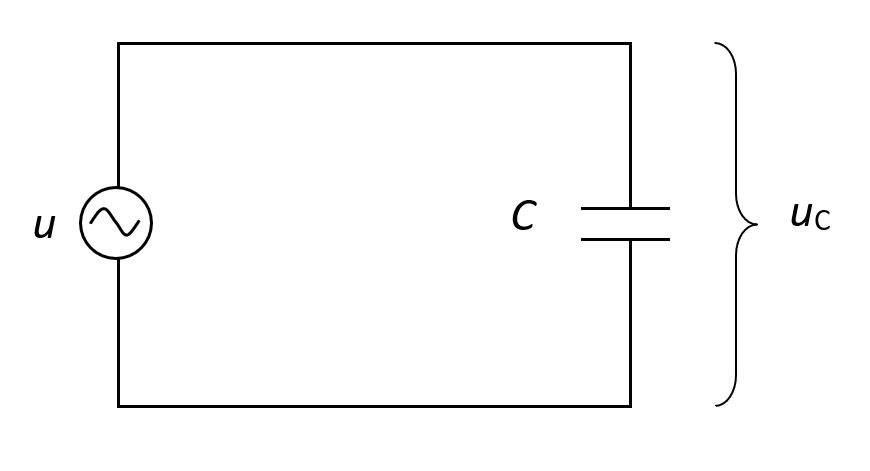
Kad se kondenzator kapaciteta C priključi na izvor istosmjernog napona, poteći će struja, kondenzator će se nabiti, struja će prestati teći i kondenzator će se nakon toga ponašati kao beskonačni otpor. Međutim, ako se kondenzator spoji na izvor izmjeničnog napona, zbog stalnog mijenjanja smjera napona, kondenzator se naizmjenično puni i prazni tako da će u krugu teći izmjenična struja. Za izmjeničnu struju kondenzator predstavlja konačni otpor.
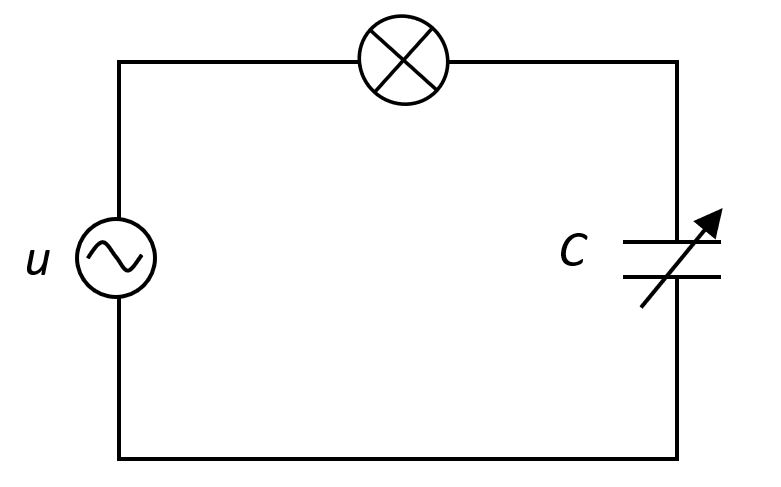
Žarulju se priključi na gradsku mrežu preko promjenjivog kondenzatora. Mijenjajući kapacitet kondenzatora promatranjem sjaja žarulje (ili mjereći struju), može se zaključiti da je kapacitivni otpor kondenzatora obrnuto proporcionalan njegovu kapacitetu.
Pokusi i računi pokazuju da je kapacitivni otpor manji što su kapacitet kondenzatora i frekvencija struje veći.
Kapacitivni se otpor računa formulom
odnosno
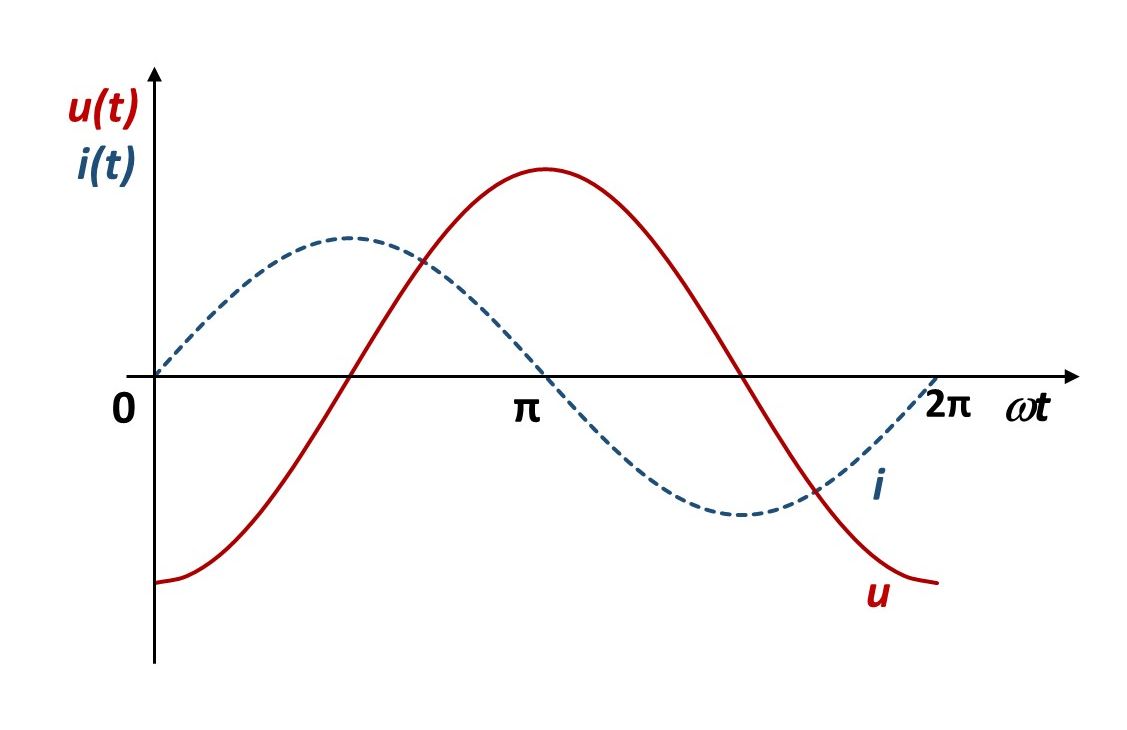
Pri punjenju kondenzatora istosmjernom strujom najprije poteče struja, a kad se kondenzator nabije, na njemu se pojavi napon. Slično je i kad kroz kondenzator prolazi izmjenična struja – napon i struja nisu u fazi. Izmjenična struja prethodi naponu za ili napon zaostaje za strujom za Fazni je pomak napona u odnosu prema struji na kapacitivnom otporu
U strujnom se krugu uz kondenzator može naći i omski otpor.
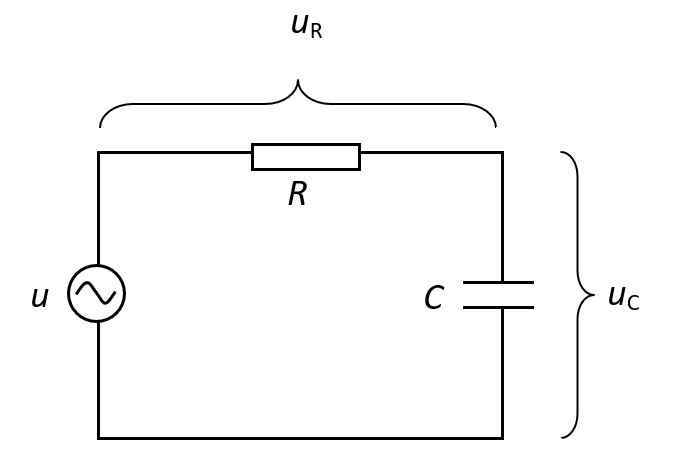
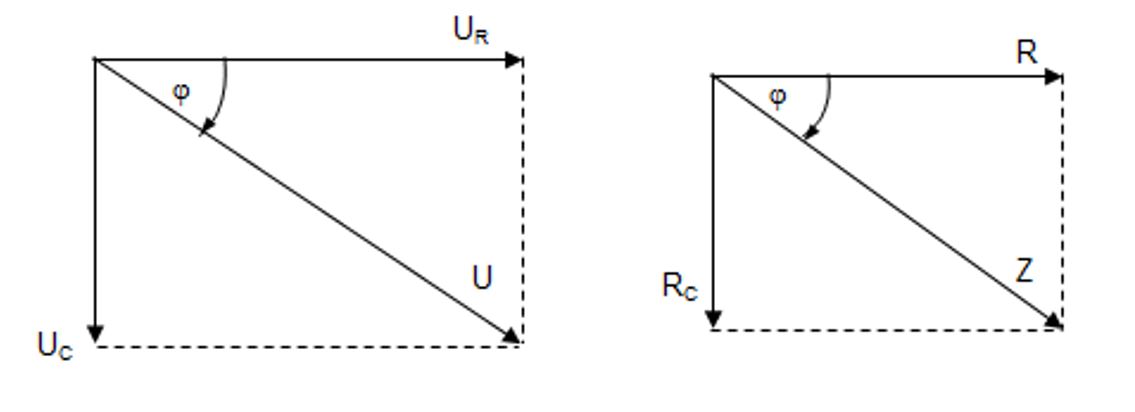
Rezultantni otpor (impedancija) dobiva se vektorskim zbrajanjem omskog i kapacitivnog otpora:
ili
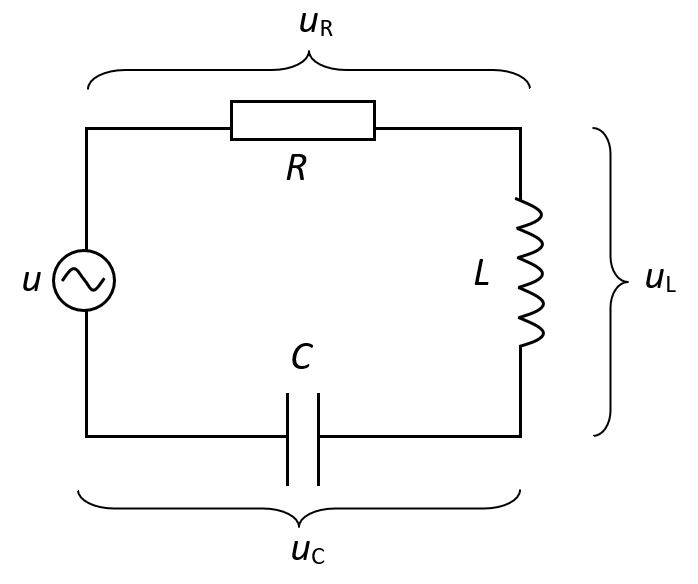
RLC strujni krug je spoj omskog, induktivnog i kapacitivnog otpora u krugu izmjenične struje.
Na omskom otporu napon je u fazi sa strujom, na induktivnom otporu napon prethodi struji za a na kapacitivnom otporu napona zaostaje za strujom za
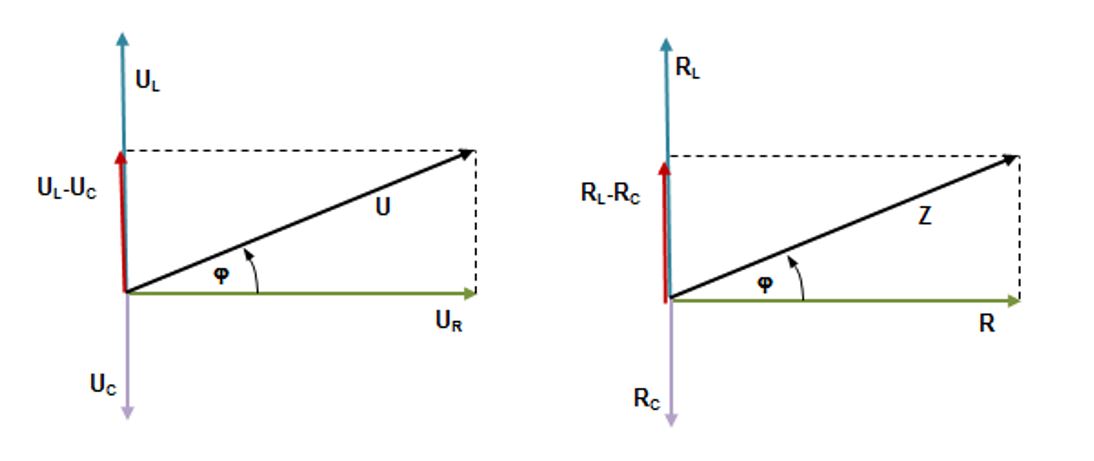
Impendancija u RLC strujnom krugu (iz vektorskog dijagrama):
tj.
Ohmov zakon za izmjeničnu struju može se pisati u istom obliku kao i za istosmjernu struju:
Fazni pomak napona u odnosu na struju:
ili
Napomena
Jakost izmjenične struje u serijskom RCL strujnom krugu dana je izrazom:
U slučaju kada su
Pojava pri kojoj RLC strujnim krugom poteče najveća struja naziva se električna rezonancija. To se može postići mijenjanjem frekvencije f ili pojedinih otpora,
Dakle, kada su induktivni i kapacitivni otpor u RLC strujnom krugu jednaki:
ω L = 1 ω C kružna je frekvencija:
ω = 1 L C , odnosno dobije se formula za frekvenciju koja se naziva Thomsonova formula:
f = 1 2 π L C .
Pri rezonanciji je impedancija jednaka omskom otporu (Z = R ), struja je maksimalna i u fazi je s naponom
Električna je rezonancija česta pojava kod elektroničkih strujnih krugova.
Vrijednost napona i struja kroz trošilo spojeno na izmjenični napon stalno se vremenski mijenjaju. Tako se mijenja i snaga te se stoga razmatra srednja snaga.
Ako je trošilo omski otpor, napon i struja su u fazi, a srednja je vrijednost snage:
P = U ef · I ef. Kada se u strujnom krugu nalazi uz omski otpor i reaktivni otpor (induktivni ili kapacitivni), napon i struja nisu u fazi. Ako je u krugu samo kondenzator, struja teče, kondenzator se puni i prazni,
ali ta struja ne obavlja rad, ne proizvodi toplinu i slično. Takva se struja naziva jalovom strujom, a snaga se naziva reaktivnom (jalovom) snagom: φ = 90 ° ,
P r = U C · I C . Iako je reaktivna snaga različita od nule, radna je snaga jednaka nuli! Slično je i s idealnom zavojnicom (omski joj je otpor zanemariv) priključenom na izmjenični napon:
P r = U L · I L .
Primjer 1.
Izmjenična struja
prolazi trošilom otpora i = 6 A s i n 314 s - 1 · t Odredimo: 650 Ω .
- frekvenciju
- najveću vrijednost struje
- efektivnu vrijednost struje.
Iz jednadžbe za izmjeničnu struju
Iz jednadžbe za izmjeničnu struju
Efektivna vrijednost struje iznosi:
Primjer 2.
Kondenzator kapaciteta
i zavojnica indukcije 40 μF serijski su spojeni na izvor izmjenične struje efektivne vrijednosti napona 0,6 H i frekvencije 110 V Ukupni radni otpor u strujnom krugu iznosi 50 Hz . Odredimo: 20 Ω .
- impedanciju strujnoga kruga
- efektivnu vrijednost struje u strujnom krugu
- pad napona na kondenzatoru.
Kapacitivni je otpor kondenzatora:
Induktivni je otpor zavojnice:
Induktivnost je strujnog kruga:
Efektivna vrijednost struje u strujnom krugu iznosi:
Pad napona na kondenzatoru je:
Primjer 3.
RLC strujni krug sastavljen je od serijski spojenih: otpornika radnog otpora
zavojnice induktivnosti R = 130 Ω , i kondenzatora kapaciteta L = 30 mH U strujnom krugu je izvor izmjeničnog napona C = 3 μF . frekvencije 50 V 50 Hz .
- Odredimo fazni kut između izmjeničnog napona i struje.
- Kolika je srednja snaga strujnoga kruga?
Kružna frekvencija iznosi:
Fazni pomak napona u odnosu na struju dobije se iz:
i iznosi
Kako bi se odredila snaga serijskog RLC strujnoga kruga, treba izračunati efektivnu struju koja teče strujnim krugom.
Jakost izmjenične struje u serijskom RCL strujnom krugu dana je izrazom:
Snaga je:
U izmjenični strujni krug serijski su spojeni zavojnica induktivnosti
Frekvencija pri kojoj će strujni krug biti u rezonanciji dobije se po Thomsonovoj formuli:
Kondenzator i otpornik otpora
Kolika je rezonantna frekvencija u RLC strujnom krugu u kojemu zavojnica ima induktivitet
U RLC krugu serijski su spojeni otpornik otpora