x
Učitavanje
  1. Matematika 8
  2. 1. Kvadriranje
  3. 1.5 Kvadrat zbroja

1.5 Kvadrat zbroja

Europska unija, Zajedno do fondova EU
Što ću naučiti?
Samostalno učenje
Procijenite svoje znanje
Sadržaj jedinice
Sadržaj jedinice
Povećanje slova
Smanjenje slova
Početna veličina slova Početna veličina slova
Visoki kontrast
a Promjena slova
  • Verdana
  • Georgia
  • Dyslexic
  • Početni
Upute za korištenje

Na početku...

Školska je pozornica u obliku kvadrata. Za potrebe školskog plesa pozornicu treba proširiti za 1 m sa svake strane. Plan nove pozornice prikazan je slikom.

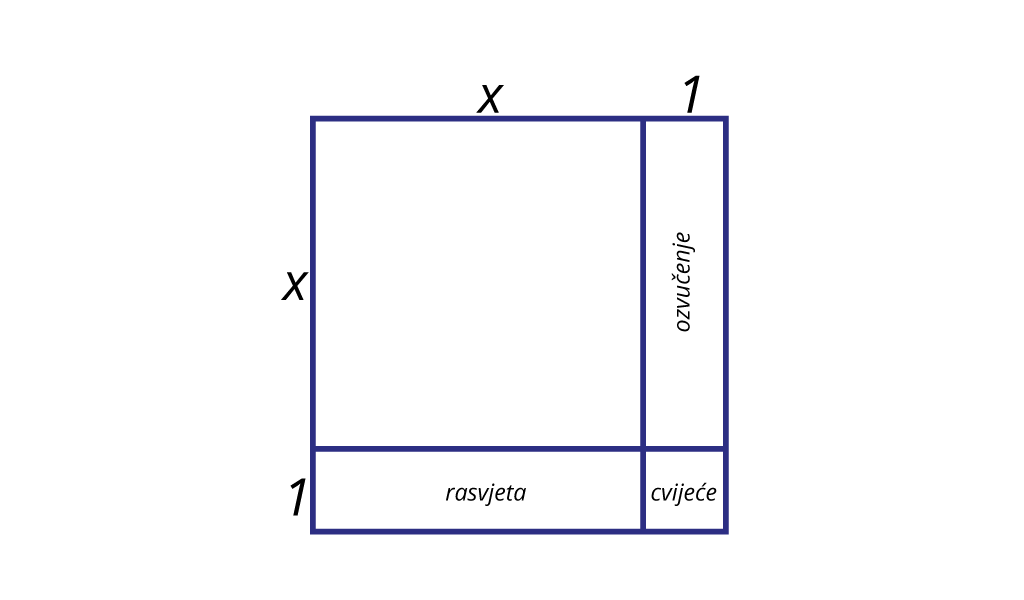
Na slici je prikazan plan proširene pozornice.

  1. Napišite na papir izraz za ukupnu površinu proširene pozornice.
  2. Napišite izraz za ukupnu površinu pozornice kao zbroj površina pojedinih dijelova proširene pozornice.
  3. Izjednačavanjem izraza iz prva dva zadatka odredite koliko je x + 1 2 ? ​
  4. Nakon nekog vremena odlučeno je da pozornicu treba proširiti ne za jedan nego za 2 metra sa svake strane. Izrazite površinu nove pozornice na dva načina (kao u a) i b) zadatku).
    1. ( x + 1 ) 2
    2. Ukupna površina pozornice iznosi x 2 + x + x + 1 = x 2 + 2 x + 1
    3. ( x + 1 ) 2 = ( x + 1 ) ( x + 1 ) = x 2 + x + x + 1 = x 2 + 2 x + 1
    4. ( x + 2 ) 2 = ( x + 2 ) ( x + 2 ) = x 2 + 2 x + 2 x + 4 = x 2 + 4 x + 4

    Kvadrat zbroja

    Dopunite izraze.

    1. x + 1 2 = x 2 + x + x + 1 = x 2 + 2 x + 1
    2. ( x + 2 ) 2 =
    3. x + 3 2 =
    4. x + 4 2 =
    5. 2 x + 1 2 =
    1. ( x + 1 ) 2 = x + 1 x + 1 = x 2 + x + x + 1 = x 2 + 2 x + 1
    2. x + 2 2 = x + 2 x + 2 = x 2 + 2 x + 2 x + 4 = x 2 + 4 x + 4
    3. x + 3 2 = x + 3 x + 3 = x 2 + 3 x + 3 x + 9 = x 2 + 6 x + 9
    4. x + 4 2 = x + 4 x + 4 = x 2 + 4 x + 4 x + 16 = x 2 + 8 x + 16
    5. ​ 2 x + 1 2 = 2 x + 1 2 x + 1 = 4 x 2 + 2 x + 2 x + 1 = 4 x 2 + 4 x + 1

    Zadatak 1.

    Promotrite prethodni zadatak. Što zamjećujete? Kako kvadriramo zbroj?

    Kad kvadriramo zbroj, dobit ćemo tročlani izraz pri čemu je prvi član jednak kvadratu prvog pribrojnika, zadnji član kvadratu drugog pribrojnika, a srednji je član jednak umnošku pribrojnika uvećanom dva puta. ​

    a + b 2 = a + b · a + b = a 2 + a b + b a + b 2 = a 2 + 2 a b + b 2  

    Provjerite preslagivanjem na kvadrat sa stranicom duljne a + b .

    Povećaj ili smanji interakciju

    Rješenje slagalice možete provjeriti u sljedećoj interakciji.

    Zbroj kvadriramo tako da zbroj kvadrata njegovih pribrojnika uvećamo za dvostruki umnožak pribrojnika. To možemo zapisati formulom:

    ( a + b ) 2 = a 2 + 2 a b + b 2

    Formula ( a + b ) 2 = a 2 + 2 ab + b 2 naziva se kvadrat zbroja.

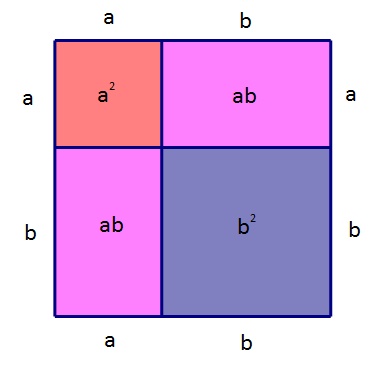
    Na slici je dan površinski prikaz kvadrata zbroja.

    Izraz se radi lakšeg pamćenja može zapisati

    p r v i + d r u g i 2 = p r v i 2 + 2 · p r v i · d r u g i + d r u g i 2

    Tada pamtimo da je kvadrat zbroja prvoga i drugog broja jednak izrazu "prvi na kvadrat više dvostruki prvi puta drugi više drugi na kvadrat".

    Primjer 1.

    Primjenom formule za kvadrat zbroja kvadrirajmo izraze.

    1. 4 + 5 x 2
    2. 1.2 a + 0.5 2
    3. 1 3 + 2 c 2
    1. ( 4 + 5 x ) 2 = 16 + 40 x + 25 x 2
    2. 1.2 a + 0.5 2 = 1.44 a 2 + 1.2 a + 0.25
    3. ( 1 3 + 2 c ) 2 = 1 9 + 4 3 c + 4 c 2

    Zadatak 2.

    Primjenom formule za kvadrat zbroja kvadrirajte izraze.

    1. 3 x y + 1 2
    2. ( 1 2 b + 3 4 ) 2
    3. ( 0.2 p + 0.1 ) 2
    1.  3 x y + 1 2 = 9 x 2 y 2 + 6 x y + 1
    2. 1 2 b + 3 4 2 = 1 4 b 2 + 3 4 b + 9 16
    3. 0.2 p + 0.1 2 = 0.04 p 2 + 0.04 p + 0.01

    Primjer 2.

    Napišimo na papir zadane izraze u obliku kvadrata zbroja.

    1. 4 a 2 + 12 a + 9
    2. 1 4 a 2 + 3 5 a b + 9 25 b 2  
    1. 4 a 2 + 12 a + 9 = 2 a + 3 2
    2. 1 4 a 2 + 3 5 a b + 9 25 b 2 = 1 2 a + 3 5 b 2

    Kolekcija zadataka 1

    Zadatak 3.

    Na papir napišite u obliku kvadrata zbroja.

    1. a 2 + 10 a + 25  
    2. 0.09 p 2 + 0.72 p + 1.44
    1. a 2 + 10 a + 25 = ( a + 5 ) 2
    2. 0.09 p 2 + 0.72 p + 1.44 = ( 0.3 p + 1.2 ) 2

    Dovucite vrijednosti na njihove jednakosti.

    ( 4 x + 3 ) 2  
    		9 x 2 + 24 x + 16  
    ( 2 + 5 y ) 2  
    		  16 x 2 + 24 x + 9
    ( 3 x + 4 ) 2
    		25 + 20 y + 4 y 2  
    ( 5 + 2 y ) 2  
    		4 + 20 y + 25 y 2  
    null
    null

    Zadatak 4.

    Kvadrirajte.

    1. ( a + 5 b ) 2
    2. ( 3 4 x + 0.1 y ) 2  
    3. ( 4 5 c + 2 3 d ) 2
    4. ( 1.1 e + 1.5 ) 2
    1. ​ ( a + 5 b ) 2 = a 2 + 10 a b + 25 b 2
    2. ​ 3 4 x + 0.1 y 2 = 9 16 x 2 + 3 20 x y + 0.01 y 2
    3. 4 5 c + 2 3 d 2 = 16 25 c 2 + 16 15 c d + 4 9 d 2
    4. 1.1 e + 1.5 2 = 1.21 e 2 + 3.3 e + 2.25
    Zatvori

    Kolekcija zadataka 2

    Zadatak 5.

    Riješi zadatke!

    1. Točno ili netočno ?

      ( 5 a ) 2 = 5 a  

      null

      Postupak:

      ( 5 a ) 2 = 5 a · 5 a = 25 a 2

    2. Točno ili netočno?

      3 a 2 = 9 a 2

      null

    3. Točno ili netočno?

      - 3 2 = 9  

      null
      null

    4. Točno ili netočno?

      7 a b 2 = 49 a b 2   

      null

      Postupak:

      7 a b 2 = 49 a 2 b 2

    5. Točno ili netočno?  

      2 a 2 = - 2 a 2

      null

    6. Točno ili netočno?

      5 a 2 = 10 a 2

      null
      null

    7. Točno ili netočno?

      a b 2 = a 2 b

      null

    8. Točno ili netočno?

      a + b 2 = a 2 + b 2

      null
      null

    9. Točno ili netočno?

      a + b 2 = a 2 + 2 a b + b 2

      null
      null

    10. Točno ili netočno?

      a + b 2 = - a - b 2

      null

      Postupak:

      - a - b 2 = - a + b 2

    11. Točno ili netočno?

      a + 4 2 = a 2 + 8 a + 16 2  

      null

       

    Zadatak 6.

    Rene je kvadrirala broj 3 2 5 . Napisala je da je ( 3 2 5 ) 2 = 9 4 25 .

    Lucija tvrdi da je to netočno jer je 3 2 5 = 3 + 2 5 te zato treba odrediti koliko je ( 3 + 2 5 ) 2 .

    Raspravi se pridružila i Irena.

    Ona tvrdi da broj 3 2 5 treba zapisati kao nepravi razlomak i onda ga kvadrirati.

    Tko ima pravo? Objasnite.

    Zapis 3 2 5  zapravo je skraćeni zapis zbrajanja 3 + 2 5 .

    Zato i Lucija i Irena imaju pravo.

    ( 3 + 2 5 ) 2 = 9 + 2 · 3 · 2 5 + 4 25 = 9 + 12 5 + 4 25 = 9 + 60 25 + 4 25 = 9 64 25 = 11 14 25  

    Također,

    ( 3 2 5 ) 2 = ( 17 5 ) 2 = 289 25 = 11 14 25 .

    Zatvori

    Kutak za znatiželjne

    Postoje li neki racionalni brojevi za koje vrijedi

    a + b 2 = a 2 + b 2 ?

    Za kvadrat zbroja vrijedi ( a + b ) 2 = a 2 + 2 ab + b 2 .

    Ako želimo da je ( a + b ) 2 = a 2 + b 2 , tada mora biti 2 ab = 0 .

    Taj će izraz biti jednak nuli samo ako vrijedi: a = 0 i/ili b = 0 .

    Primjer 3.

    Primjenom formule za kvadrat zbroja izračunajmo 91 2 na najjednostavniji način.

    Broj 91 zapisat ćemo kao 90 + 1 .

    Tada je 91 2 = ( 90 + 1 ) 2 = 90 2 + 2 · 90 · 1 + 1 2 = 8 100 + 180 + 1 = 8 281 .

    Kolekcija zadataka 3

    Zadatak 7.

    Primjenom formule za kvadrat zbroja izračunajte kvadrat broja na najjednostavniji način.

    1. 71 2  
    2. 62 2
    3. 51 2

    1. 71 2 = ( 70 + 1 ) 2 = 70 2 + 2 · 70 · 1 + 1 2 = 4 900 + 140 + 1 = 5 041
    2. 62 2 = ( 60 + 2 ) 2 = 60 2 + 2 · 60 · 2 + 2 2 = 3 600 + 240 + 4 = 3 844
    3. 51 2 = ( 50 + 1 ) 2 = 50 2 + 2 · 50 · 1 + 1 2 = 2 500 + 100 + 1 = 2 601

    Pogodite moj broj 2 - matematički trik

    Na papir zapišite prirodni broj od 1 do 20 . ​

    Pribrojite mu 1 . ​

    Dobiveni zbroj kvadrirajte. ​

    Kvadratu zbroja pribrojite 4 . ​

    Od dobivenog zbroja oduzmite broj koji ste zamislili. ​

    Dobivenoj razlici pribrojite broj 5 . ​

    Od dobivenog zbroja oduzmite svoj broj. ​

    U kvadratić upišite dobiveni rezultat.​

    Povećaj ili smanji interakciju

    Zadatak 8.

    Objasnite trik Pogodite moj broj 2  koristeći se algebarskim izrazima.

    Neka je zamišljeni prirodni broj od 1 do  20 broj x . ​

    Pribrajanjem broja 1 dobivamo izraz x + 1 .

    Kvadriranjem zbroja dobivamo izraz x 2 + 2 x + 1 .

    Pribrajanjem broja 4 dobivamo izraz x 2 + 2 x + 5 .

    Nakon što od dobivenog zbroja oduzmemo zamišljeni broj dobivamo izraz x 2 + x + 5 .

    Uvećavanjem dobivene razlike za broj 5 dobivamo izraz x 2 + x + 10 .

    Umanjivanjem dobivenog zbroja za zamišljeni broj dobivamo izraz x 2 + 10 .

    Kako bismo, nakon što se upiše dobivena razlika, odredili zamišljeni broj, upisani broj treba umanjiti za 10 , a zatim odrediti koji broj pomnožen samim sobom daje dobivenu razliku. ​

    Zadatak 9.

    Na slici je dan površinski prikaz kvadrata binoma.

    Povećamo li svaku stranicu kvadrata za 3 cm , dobit ćemo kvadrat čija je površina za 39 cm 2 veća od površine početnog kvadrata. Kolika je duljina stranice početnog kvadrata? ​

    x 2 + 39 = ( x + 3 ) 2

    x 2 + 39 = x 2 + 6 x + 9

    39 = 6 x + 9

    39 - 9 = 6 x

    30 = 6 x

    x = 5

    Duljina je stranice početnog kvadrata 5 cm .

    Zatvori

    ...i na kraju

    Naučili smo kako kvadrirati zbroj dvaju pribrojnika. Zbroj dvaju pribrojnika kvadriramo tako da zbroj kvadrata njegovih pribrojnika uvećamo za dvostruki umnožak pribrojnika, tj.

    a + b 2 = a 2 + 2 a b + b 2 .

    Ako želite proširiti svoje znanje, otkrijte formulu za kvadrat zbroja triju brojeva (trinoma). Želite li možda istražiti i Pascalov trokut te otkriti gdje se u njemu skriva formula za kvadrat binoma?

    PROCIJENITE SVOJE ZNANJE

    1

    Koji od navedenih izraza odgovara kvadratu zbroja ( 3 x + 7 ) 2 ?

    null
    null
    2
    Upišite srednji član kvadriranog izraza.
    2 5 + c 2 = 4 25 +   + c 2  
    (Za razlomak upotrijebite kosu crtu.)
    null
    null
    3
    Upišite posljednji član kvadriranog izraza ( 0.6 x + 3 ) 2 = 0.36 x 2 + 3.6 x +  .
    null
    null
    4
    Dopunite. x 2 + 12 x +   = ( x + ) 2 . ​
    null
    null
    5

    Kvadriranjem izraza ( a + b ) 2 dobivamo a 2 + b 2 .

    null
    null
    6
    Primjenjujući formulu za kvadrat zbroja, izračunajte 71 2 .
    null
    null
    7

    Ako je x = - 2 , tada je vrijednost izraza ( x - 2 ) 2  od vrijednosti izraza ( x - 1 ) ( x - 2 ) .

    null
    null
    ZAVRŠITE PROCJENU

    Idemo na sljedeću jedinicu

    1.6 Kvadrat razlike