x
Učitavanje
  1. Matematika 8
  2. 1. Kvadriranje
  3. 1.6 Kvadrat razlike

1.6 Kvadrat razlike

Europska unija, Zajedno do fondova EU
Što ću naučiti?
Samostalno učenje
Procijenite svoje znanje
Sadržaj jedinice
Sadržaj jedinice
Povećanje slova
Smanjenje slova
Početna veličina slova Početna veličina slova
Visoki kontrast
a Promjena slova
  • Verdana
  • Georgia
  • Dyslexic
  • Početni
Upute za korištenje

Na početku...

Obitelj Štedić uređuje apartman na moru. Apartman se sastoji od četiriju prostorija, a njegov je tlocrt prikazan na slici. Gospođa i gospodin Štedić trebaju izračunati površinu dnevnog boravka kako bi postavili nove podne obloge.

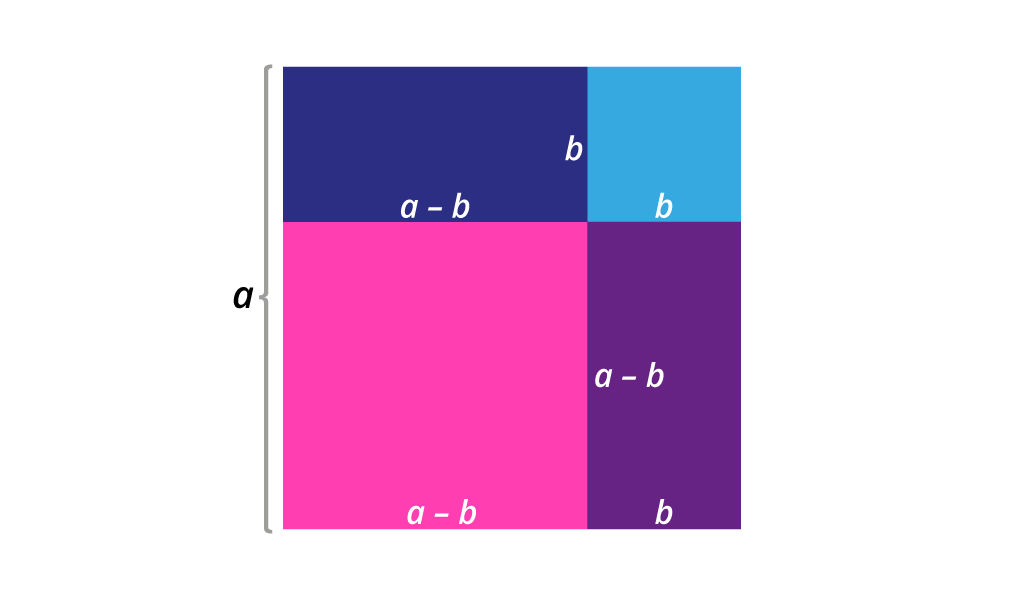
Ilustracija prikazuje tlocrt apartmana u obliku kvadrata. Kvadrat sa stranicom duljine a podijeljen je na dva kvadrata i dva pravokutnika.

Dnevni boravak ima oblik kvadrata sa stranicom duljine a - b .

Gospođa Štedić izrazila je površinu dnevnog boravka kao razliku ukupne površine apartmana i površine preostalih triju prostorija.

a 2 = a - b 2 + 2 b a - b + b 2

( a - b ) ² = a ² - 2 ab + 2 b ² - b ²

a - b 2 = a 2 - 2 a b + b 2

Što mislite, je li postupak kojim se koristi gospođe Štedić dobar? Provjerite postupak ako znamo da je riječ o apartmanu površine 64 m 2 te da je duljina zida manjeg kvadrata jednaka 3 m .

Kvadrat razlike dvaju racionalnih brojeva

Izračunajmo sada kvadrat razlike dvaju racionalnih brojeva.

( a - b ) 2 = ( a - b ) · ( a - b ) = a 2 - a b - b a + b 2 = a 2 - 2 a b + b 2  

Dakle, možemo pisati:

( a - b ) 2 = a 2 - 2 a b + b 2 .

U zagradi je razlika dvaju brojeva koju treba kvadrirati.

Potrebno je izračunati kvadrat razlike dvaju brojeva pa zbog toga formulu nazivamo kvadrat razlike.

Radi lakšeg pamćenja možemo izreći i ovako:

p r v i - d r u g i 2 = p r v i 2 - 2 · p r v i · d r u g i + d r u g i 2 .  

Čitamo: "Kvadrat razlike prvog i drugog broja jednak je prvi na kvadrat minus dvostruki prvi puta drugi plus drugi na kvadrat."

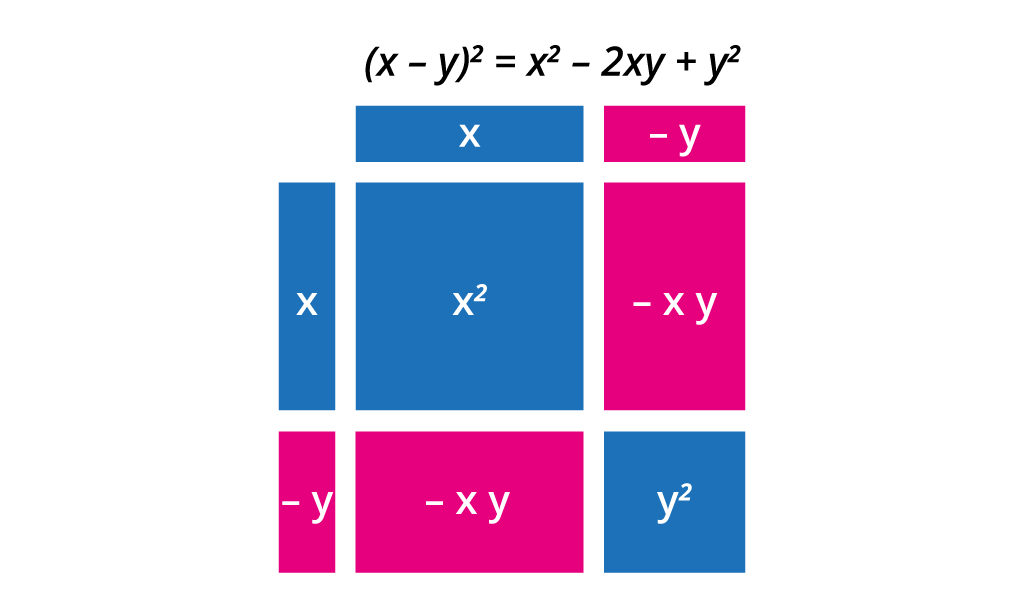
Ilustracija prikazuje algebarske pločice za prikaz kvadrata razlike.

Primijenimo sada dobivenu formulu na nekoliko primjera.

Formulu možemo upotrijebiti za računanje kvadrata razlike.

Primjer 1.

Kvadrirajmo razlike koristeći se formulom za kvadrat razlike.

  1. a - 5 2
  2. ( 3 x - 2 ) 2  
  3. ( 0.1 c - 1.5 d ) 2  
  4. 2 3 a - 3 4 b 2
  1. a - 5 2 = a 2 - 2 · a · 5 + 5 2 = a 2 - 10 a + 25
  2. ( 3 x - 2 ) 2 = ( 3 x ) 2 - 2 · 3 x · 2 + 2 2 = 9 x 2 - 12 x + 4
  3. ( 0.1 c - 1.5 d ) 2 = ( 0.1 c ) 2 - 2 · 0.1 c · 1.5 d + ( 1.5 d ) 2 = 0.01 c 2 - 0.3 c d + 2.25 d 2
  4. 2 3 a - 3 4 b 2 = 2 3 a 2 - 2 · 2 3 a · 3 4 b + 3 4 b 2 = 4 9 a 2 - a b + 9 16 b 2
… ili za zapisivanje trinoma u obliku kvadrata.

Primjer 2.

Napišimo na papir u obliku kvadrata.

  1. a² - 8 a + 16
  2. 25 b 2 - 30 b + 9
  3. 0.01 - 0.22 x + 1.21 x 2
  4. 9 25 z 2 - 4 3 z y + 100 81 y 2  
  1. a 2 - 8 a + 16 = ( a - 4 ) ²
  2. 25 b 2 - 30 b + 9 = 5 b - 3 2
  3. 0.01 - 0.22 x + 1.21 x 2 = 0.1 - 1.1 x 2
  4. 9 25 z 2 - 4 3 z y + 100 81 y 2 = 3 5 z- 10 9 y 2

Kolekcija zadataka 1

Zadatak 1.

Koristeći se pravilom za kvadrat razlike, riješite zadatke.

Zadatke rješavajte koristeći se algebarskim pločicama.

Prisjetite se da crvene pločice možete dobiti pritiskom na bilo koju od postojećih pločica. Na isti način i vraćate polaznu boju pločice.

Povećaj ili smanji interakciju

Zadatak 2.

  1. Izraz b - 5 2 jednak je izrazu:

    null
    null
  2. Izraz ( 4 x - 7 y ) 2   jednak je izrazu:

    null
    null

  3. Izraz ( 6 u - 5 v ) 2 jednak je izrazu:

    null
    null
Zatvori

Kolekcija zadataka 2

Zadatak 3.

  1. Izraz ( 6 c - 9 d ) 2 jednak je izrazu:

    null
    null
  2. Izraz​ ( 0.3 a - 3.5 b ) 2 jednak je izrazu:

    null
    null

  3. Dovucite odgovarajuće algebarske izraze na njihove jednakosti.

    16 - 80 x + 100 x 2
    		8 - 10 x 2
    4 - 40 x + 100 x 2
    		4 - 10 x 2
    64 - 160 x + 100 x 2
    		​ ( 2 - 10 x ) 2
    null
    null

  4. Izraz 1 - 26 e + 169 e 2 jednak je izrazu:

    null
    null

  5. 6 a - 5 b 2  zapisan u obliku trinoma jednak je:

    null
    null

Zadatak 4.

Pojednostavnite algebarske izraze.

  1. 2 a - 3 2 - 3 a 2 - 10
  2. 2 x - 5 2 + x - 2 2  

  1. 2 a - 3 2 - 3 a 2 - 10 = 4 a 2 - 12 a + 9 - 3 a 2 - 10 = a 2 - 12 a - 1
  2. 2 x - 5 2 + x - 2 2 = 4 x 2 - 20 x + 25 + x 2 - 4 x + 4 = 5 x 2 - 24 x + 29
Zatvori

Kolekcija zadataka 3

Zadatak 5.

Koji izraz dobivate nakon kvadriranja i pojednostavnjivanja algebarskog izraza​ 3 b - 1 2 - 2 b - 3 2 ?

Pomoć:

Pažljivo s predznacima! Prvo kvadrirajte, a onda mijenjajte predznake.

Postupak:

3 b - 1 2 - 2 b - 3 2 = 9 b 2 - 6 b + 1 - 4 b 2 - 12 b + 9 =

9 b 2 - 6 b + 1 - 4 b 2 + 12 b - 9 = 5 b 2 + 6 b - 8

Zadatak 6.

Koji izraz dobivate nakon pojednostavnjivanja algebarskog izraza 2 a - 3 2 - a + 3 2 ?

Pomoć:

2 a - 3 2 - a + 3 2 = 2 a 2 - 6 a + 9 - a 2 + 6 a + 9 =

2 a 2 - 12 a + 18 - a 2 - 6 a - 9 = a 2 - 18 a + 9

null
Zatvori

Kutak za znatiželjne

Kolekcija zadataka 4

Zadatak 7.

Zbroj kvadrata triju uzastopnih neparnih prirodnih brojeva iznosi 515 .

Koji su to brojevi?

Označimo li s n srednji od tih brojeva, onda je prvi (najmanj) broj jednak n - 2 , a treći (najveći) broj je n + 2 . Uvjet zadatka možemo zapisati u obliku

n - 2 2 + n 2 + n + 2 2 = 515 .

Kvadriranjem i sređivanjem redom dobivamo:

n 2 - 4 n + 4 + n 2 + n 2 + 4 n + 4 = 515  

3 n 2 + 8 = 515 ⇔ 3 n 2 = 507 ⇔ n 2 = 169 .

Jedini prirodni broj koji zadovoljava uvjet da je njegov kvadrat jednak 169 je broj 13 .

Rješenje je trojka neparnih prirodnih brojeva: 11 , 13 i 15 .

Zadatak 8.

Zbroj kvadrata triju uzastopnih parnih brojeva iznosi 2 708 . ​

Koji su to brojevi?

Kako broj rješenja zadatka ovisi o skupu iz kojeg uzimamo brojeve?

Označimo li s n srednji od tih brojeva, onda je prvi (najmanj) broj jednak n - 2 , a treći (najveći) broj je n + 2 . Uvjet zadatka možemo zapisati u obliku​

n - 2 2 + n 2 + n + 2 2 = 2 708 .

Kvadriranjem i sređivanjem redom dobivamo:

n 2 - 4 n + 4 + n 2 + n 2 + 4 n + 4 = 2 708

3 n 2 + 8 = 2 708 ⇔ 3 n 2 = 2 700 ⇔ n 2 = 900 .

Brojevi koji kvadrirani daju 900 su 30 i - 30 .

Ako je riječ o prirodnim brojevima, onda je rješenje trojka parnih prirodnih brojeva: 28 , 30 i 32 . Ako je riječ o cijelim brojevima, onda su rješenja dvije trojke neparnih prirodnih brojeva: 28 , 30 i 32 te - 32 , - 30 i - 28 .

Zadatak 9.

Kvadrat razlike nekih dvaju racionalnih brojeva iznosi 25 , a umnožak je tih brojeva 4 . Koliki je zbroj kvadrata tih brojeva?​

Ako je ​ a - b 2 = 25 , onda je a 2 - 2 a b + b 2 = 25 . Uvrstimo li uvjet da je a b = 4 dobivamo:

a 2 - 2 a b + b 2 = a 2 - 2 · 4 + b 2 = 25

pa je a 2 + b 2 = 25 + 8 = 33 .

Zatvori

...i na kraju

Naučili smo kako kvadrirati razliku dvaju pribrojnika.

Razliku dvaju pribrojnika kvadriramo tako da zbroj kvadrata dvaju pribrojnika umanjimo za dvostruki umnožak pribrojnika, tj.

a - b 2 = a 2 - 2 a b + b 2

Kako biste kvalitetnije usvojili naučeno gradivo, riješite zadatke koje prikazuje video.

Idemo na sljedeću jedinicu

1.7 Razlika kvadrata