


Bijela svjetlost, poput sunčeve svjetlosti, zapravo nije bijela. Unutar bijele svjetlosti nalazi se spektar duginih boja u obliku valova. Pojedinačne se boje vide se kad bijela svjetlost prolazi kroz optičku prizmu koja razdvaja valove prema njihovoj valnoj duljini i tvori dugu. Svjetlosni valovi mogu se prikazati grafom funkcije sinus.
Funkciju sinus definirali smo pomoću brojevne kružnice. Podsjetimo se definicije funkcije sinus.
Točka na brojevnoj kružnici ima koordinate (
Neka je proizvoljan realan broj. njemu odgovarajuća
Vrijednost je funkcije kosinus
Možemo li pomoću definicije nacrtati graf funkcije sinus?
Pogledajte sljedeću simulaciju.
Točka
na kružnici je pomična. Pomicanjem točke
točka
ostavljat će trag. Taj je trag graf funkcije sinus. Svaka točka na tom grafu ima koordinate
Pomoću simulacije pokušajte odgovoriti na niz pitanja o ponašanju grafa funkcije sinus.
Brojevi oblika
nultočke su funkcije sinus.
Funkcija sinus maksimum poprima za
Na intervalu od
funkcija sinus
Na intervalu od
funkcija sinus
Period je funkcije sinus:
Svojstva funkcije sinus
Funkcija ima sljedeća svojstva:
- Nultočke funkcije brojevi su
- Za sve brojeve oblika funkcija poprima maksimalnu vrijednost jednaku Za sve brojeve oblika funkcija poprima minimalnu vrijednost jednaku
- Period funkcije iznosi
- Tijek je funkcije na intervalu sljedeći:
Odredite je li funkcija na intervalu rastuća ili padajuća.
Ponašanje funkcije jednako je onom na intervalu
pa je funkcija na tom dijelu rastuća.
Nacrtajte funkciju sinus pomoću sljedećih uputa:
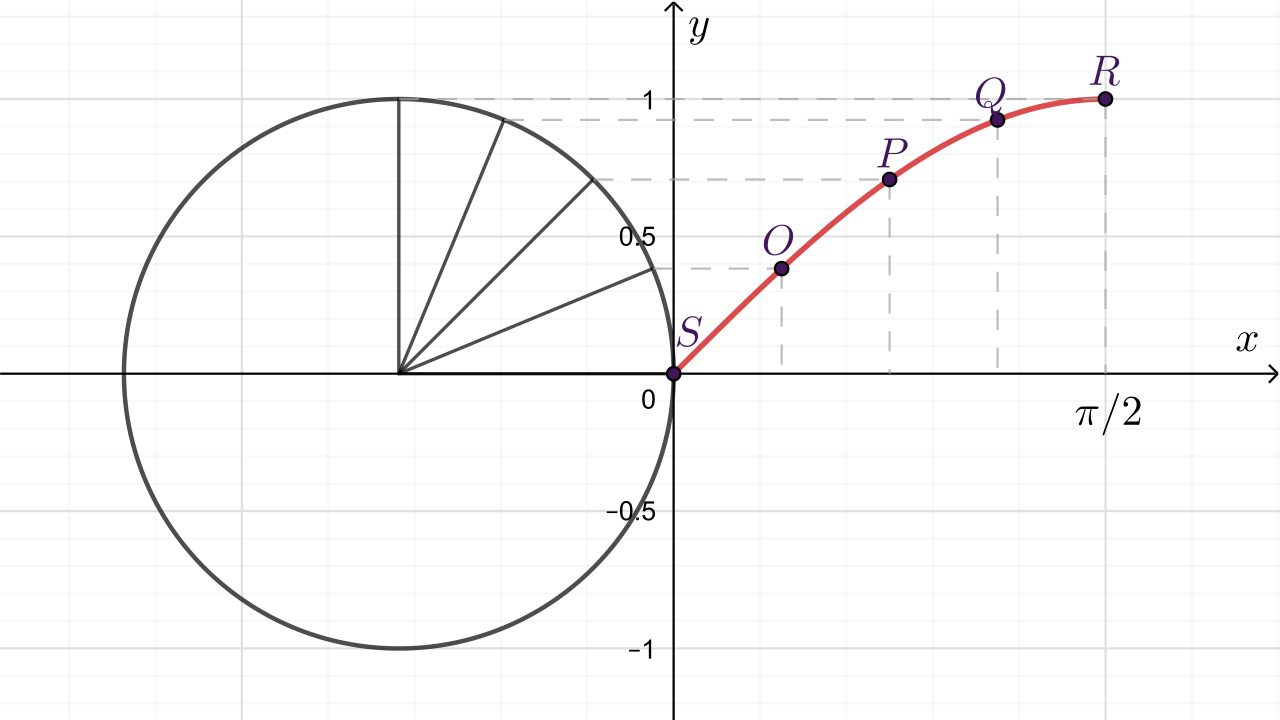
Graf funkcije sinus možemo nacrtati koristeći njezina svojstva.
Popunite tablicu.
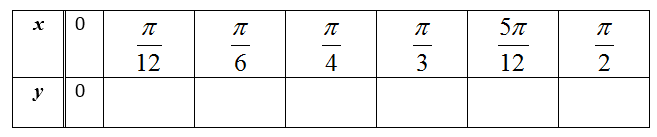
Vrijednosti iz tablice ucrtajte u koordinatni sustav i povežite glatkom krivuljom. Nacrtali ste prvi dio krivulje.
Sada se prisjetimo identiteta
Kako nam to pomaže pri crtanja grafa?
Vrijednosti funkcije sinus podudaraju se za različite argumente.
Dio grafa
Sada nacrtajte dio grafa od do koristeći se simetrijom.
Kako izgleda funkcija sinus lijevo od točke
Sjetimo se još jednog svojstva funkcije sinus.
Funkcija sinus je
Funkcija sinus je periodična s periodom:
Već smo nacrtali funkciju sinus u intervalu Zbog njezine periodičnosti, možemo nacrtati i ostatak.
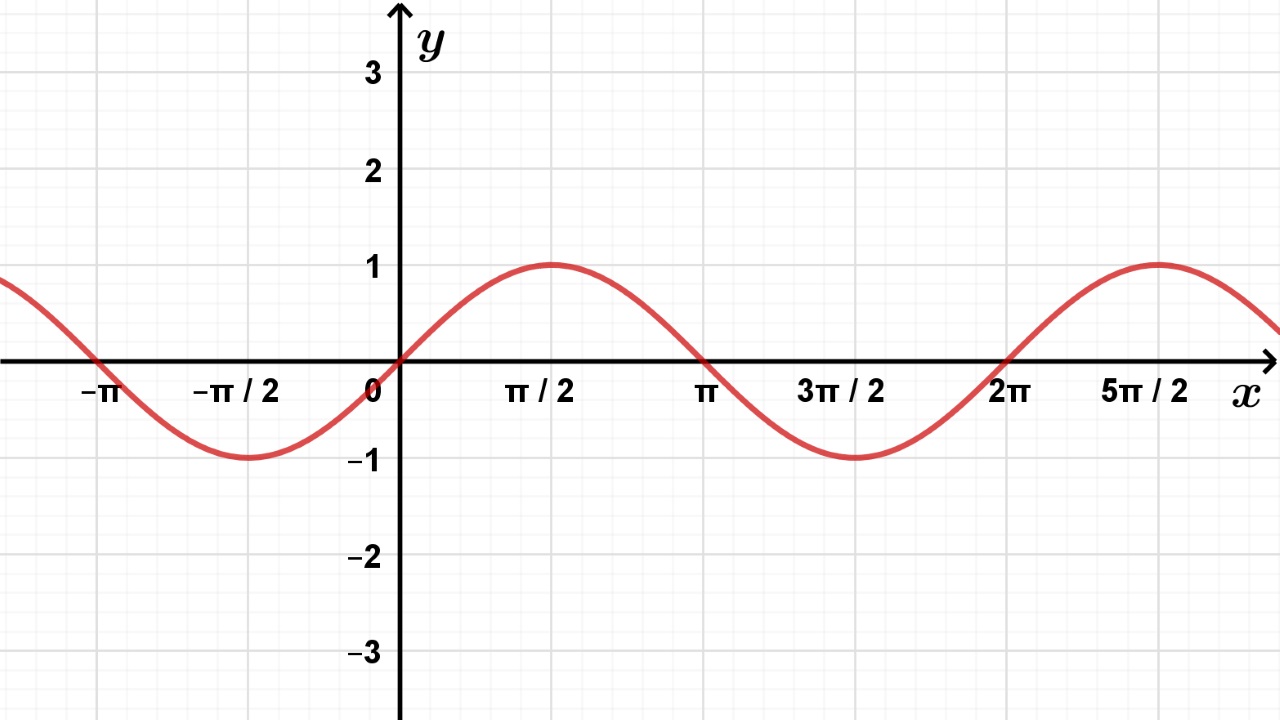
Sinusoida
Graf funkcije nazivamo sinusoida.
U sljedećoj simulaciji proučite graf funkcije
pri čemu je
pozitivna konstanta koju zovemo amplituda.
Mijenjajući koeficijent
pokušajte pronaći odgovor na pitanja.
Ako je onda je amplituda funkcije
Ako je onda je amplituda funkcije
Promjena vrijednosti amplitude za funkciju
ima utjecaj na promjenu:
Funkcija
maksimalnu vrijednost jednaku
(na intervalu
) postiže za:
U sljedećoj simulaciji pogledajte graf funkcije
pri čemu je
kružna frekvencija, te odgovorite na pitanja.
Promjena koeficijenta
utječe na promjenu amplitude funkcije
Promjena koeficijenta
utječe na promjenu perioda funkcije
Period funkcije
iznosi:
Ako je onda je period funkcije
Ako je period funkcije
Zadana je funkcija pr čemu koeficijent zovemo fazni pomak.
Kroz simulaciju usporedbe funkcije i proučite sličnosti i razlike ovih dvaju grafova te odgovorite na pitanja.
Promjena parametra
u funkciji
utječe na:
Nultočke funkcije na intervalu iznose:
Pomak funkcije
u odnosu na
jednak je
Amplituda, period i pomak sinusoide
Graf funkcije skiciramo uz pomoć grafa
Za funkciju potrebno je odrediti amplitudu, period i pomak.
- Maksimalna tj. minimalna vrijednost funkcije jednaka je tj. pa se graf funkcije nalazi između pravaca i
- Period funkcije jednak je a nultočke se nalaze na početku i na kraju tog intervala i u polovištu.
- Nultočke funkcije rješenje su jednadžbe
Za dobijemo što je pomak funkcije.
Istražite kako na graf funkcije utječe parametar
Parametar
određuje pomak grafa funkcije po osi
, tj. vertikalni pomak.
Pogledajte sada kako pomoću svega što smo naučili skicirati graf funkcije
Sinusoidom možemo prikazati promjene kod različitih pojava:

Prema mjerenjima broj sati dnevne svjetlosti nekog području 21. lipnja 2016. godine bio je 17,48 sati, a broj sati dnevnog svjetla 21. prosinca 2016. godine bio je 7,08 sati.
Odredite sinusoidni model za broj sati dnevne svjetlosti
u 2016. kao funkcije vremena
Funkcija je