

Sjetimo se grafičkog prikaza izmjenjivanja plime i oseke u Rijeci iz prošloga modula. Biste li mogli nacrtati graf funkcije koji prikazuje izmjenu plime i oseke unutar 12 sati? Na kraju jedinice, u kojoj ste crtali graf funkcije sinus, nabrojane su neke pojave koje možemo prikazati sinusoidom kao što je gibanje točke na kotaču, gibanje opruge, rad srčanog mišića...

Pokušajmo neke od pojava/gibanja u prirodi prikazati sinusoidom.

London Eye panoramski je vrtuljak u središtu Londona. Smješten je uz rijeku Temzu prekoputa Westminsterske palače. Otvoren je kao privremena atrakcija (uz dozvolu na 5 godina) 31. prosinca 1999., u povodu novog tisućljeća. Kada je otvoren, bio je najviši vrtuljak na svijetu. Ubrzo je dobio status trajne atrakcije koju je do sada posjetilo preko 30 milijuna posjetitelja.
London Eye ima 32 kapsule u koju može stati do 25 osoba. Promjer kotača je
a cijela konstrukcija visoka je
Pogledajte sljedeću animaciju kretanja kapsule na London Eye-u. Gibanje je prikazano u koordinatnom sustavu tako da os apscise predstavlja vrijeme, a os ordinate visinu koju kapsula dostigne prilikom rotacije kotača nakon vremena Promatrajmo visinu na koju se kapsula diže od mjesta ulaska u kapsulu. Inače, kotač ne staje, već se, tijekom sporog kretanja, turisti na najnižoj točki ukrcavaju u kapsulu. Brzina kretanja kotača je u sekundi.
Razmislite i odgovorite!
Za sinusoidu oblika
povežite oznake s pripadajućim pojmovima.
|
|
vertikalni pomak |
|
|
kružna frekvencija |
|
|
amplituda |
|
|
fazni pomak |
Odredimo trigonometrijski model kojim se može prikazati gibanje kapsule prilikom rotacije London Eye-a.
I, na kraju, istražimo koliki je pomak po osi apscisa.
Sada možemo izračunati fazni pomak
Iz prikaza
izjednačimo dobiveni pomak s izrazom
Kako glasi funkcija kojom možemo prikazati vožnju u London Eye-u?
Nultočke postoje. To su ujedno i minimumi funkcije. Graf na intervalu duljine temeljnog perioda sadrži dvije nultočke, odnosno dva minimuma i jedan maksimum.
i minimum iznosi
i maksimum iznosi
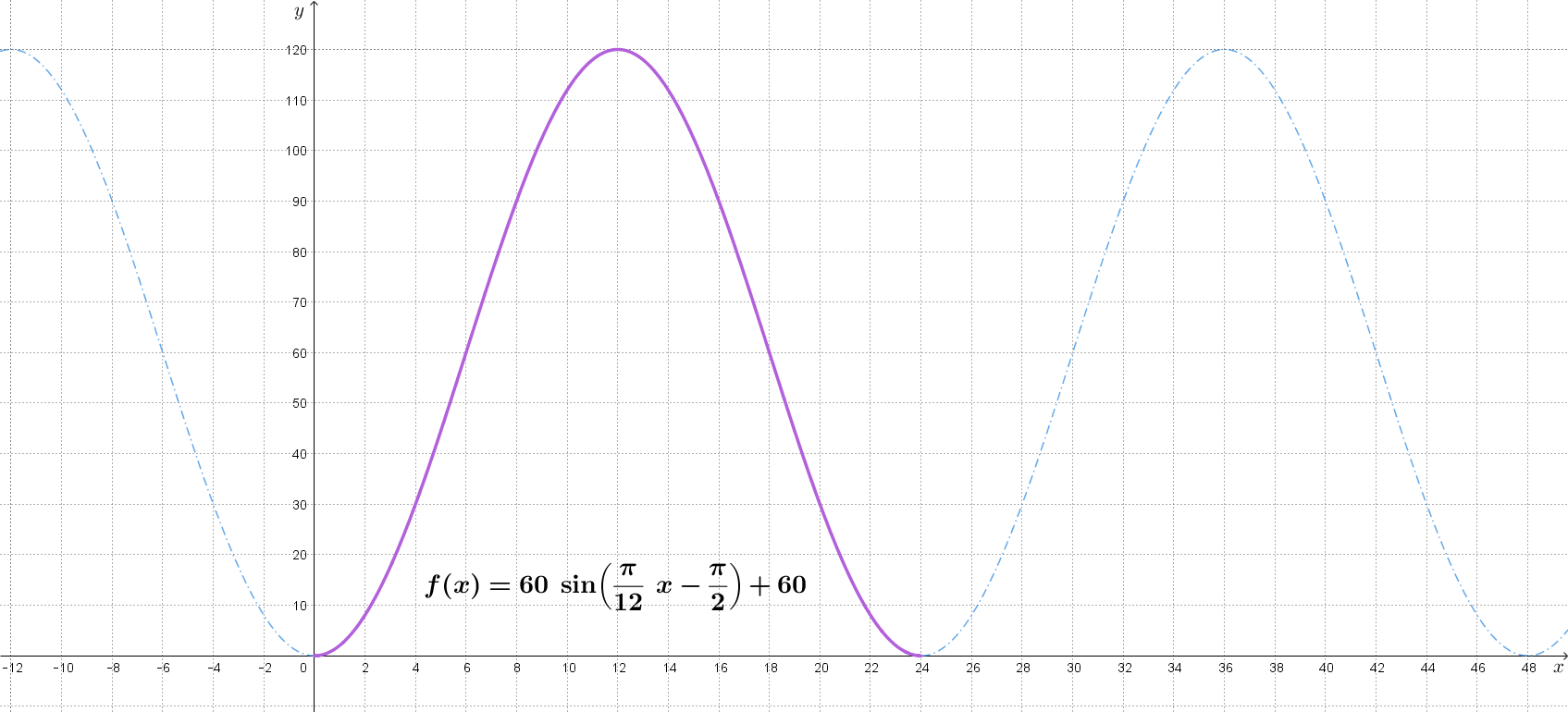
Uz pomoć rješenja iz prethodnog zadatka odgovorite na sljedeća pitanja.
Istražimo
Znate li što je Ferissov kotač? London Eye jedan je od svjetski najpoznatijih Ferissovih kotača. Istražite povijest Ferissovog kotača, kako je i kada nastao sam pojam. Potražite najpoznatije svjetske Ferissove kotače te, uz pronalazak određenih karakteristika, pokušajte odrediti funkciju koja opisuje njihovo gibanje u ovisnosti o vremenu. Prikažite grafički. Kod grafičkog prikaza omjer koordinatnih osi ne mora uvijek biti
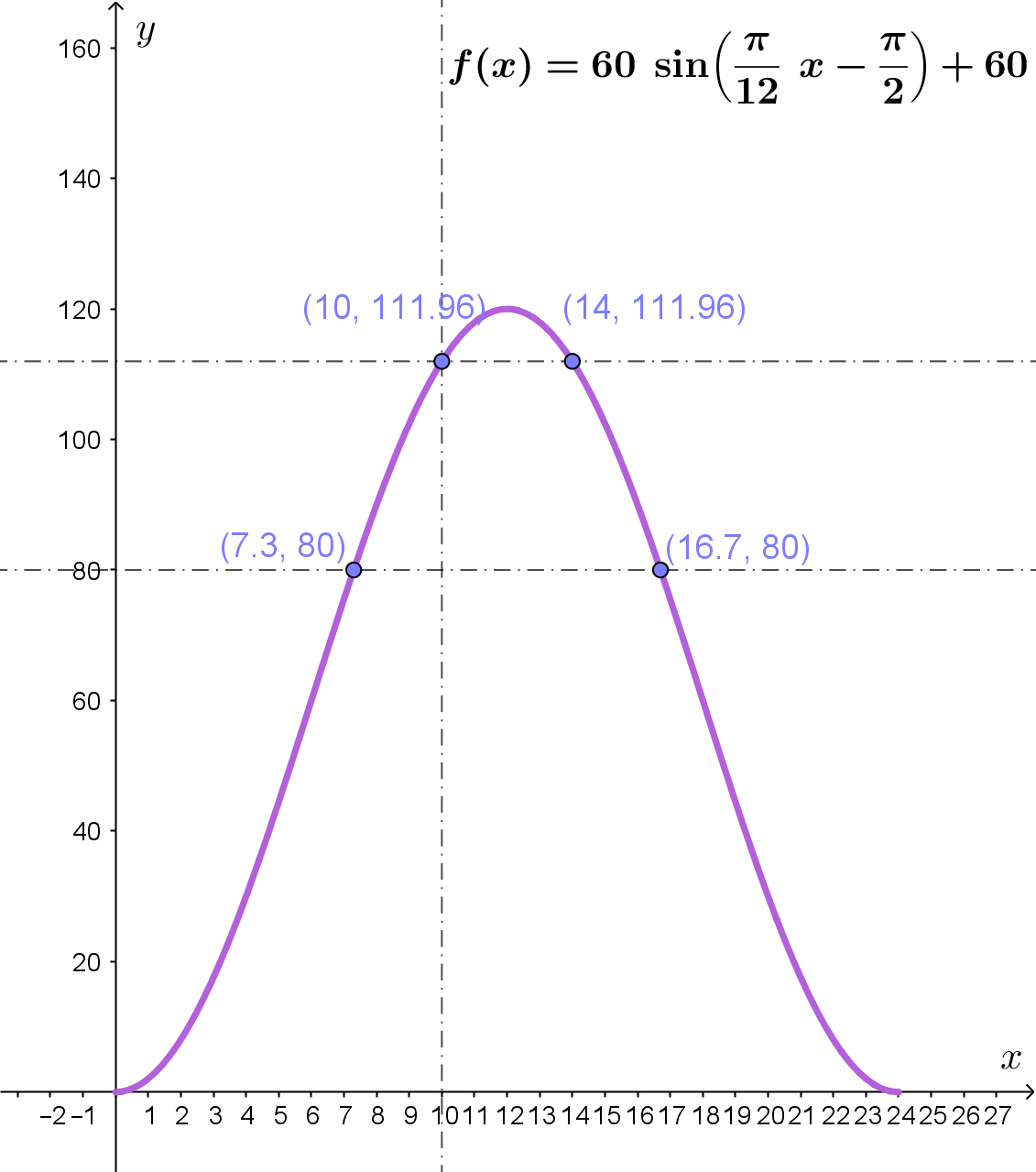
Koja funkcija pripada danoj sinusoidi?
Što je zajedničko sinusoidama iz prethodnog zadatka?
Funkcijama pridružite pripadajući temeljni period.
|
|
|
|
|
|
|
|
Imaju li sve tri funkcije isti maksimum?
Poprimaju li sve funkcije maksimum u istim točkama?
Za svaku funkciju odredite nultočke i ekstremne vrijednosti, a zatim odgovorite na sljedeća pitanja.
Primjer 1.
Toni je odlučio napraviti pauzu i otići biciklom do prijatelja. Ubrzo mu je tijekom vožnje na kotaču ostao zalijepljen papirić. Zastao je i dobio ideju za projektni zadatak iz matematike. Treba pronaći primjer u prirodi koje se može opisati nekom trigonometrijskom funkcijom. Došao je do prijatelja i uz malo mjerenja i zaokruživanja, da bi se dobio "lijep" rezultat, osmislio je zadatak. Udaljenost papirića od pločnika može se modelirati funkcijom U trenutku papirić je na pola puta između pločnika i njene maksimalne visine (polumjer kotača). Maksimalnu udaljenost od pločnika koja iznosi dostiže nakon sekundi. Treba odrediti funkciju
Uz pomoć sljedećih potpitanja modelirajmo trigonometrijsku funkciju i potražimo rješenje ovog primjera.
Nakon koliko vremena će papirić iz prethodnog primjera biti u dodiru s pločnikom s obzirom na zadani početak mjerenja?
Budući da se radi o
kruga, odgovor je nakon
Pokušajte modelirati izmjenu plime i oseke unutar 12 sati. Aktualne podatke potražite na stranicama Instituta za oceanografiju i ribarstvo.
Prisjetimo se podataka za Rijeku, dok nove podatke o plimi i oseki možete pronaći na stranicama Sportsko ribolovne udruge Marlera.
6. 11. 2019. u ponoć je razina mora bila u 4:36 i u 11:12 Kojom biste trigonometrijskom funkcijom modelirali ovu pojavu? Odaberite neke druge intervale od 12 sati za modeliranje jedne izmjene plime i oseke u danu.
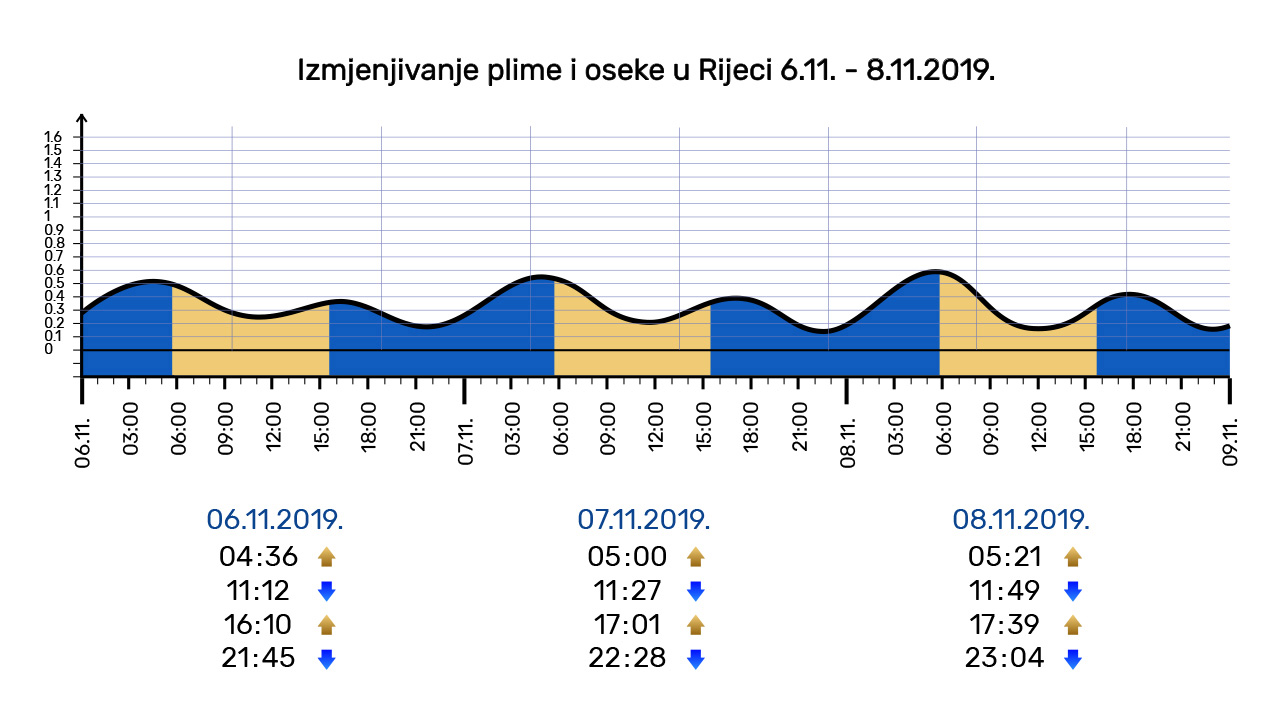
Uzmimo da je u intervalu od 12 sati (period) oseka bila 2 puta i to te plima jednom Iz tih podataka lako dobijemo Kako su nam zadana tri ekstrema, ovu pojavu ćemo lakše prikazati pomoću funkcije kosinus s temeljnim periodom 12. Sada još trebamo izračunati ako pomaknemo sinusoidu za po osi ordinata (aritmetička sredina ekstrema) konačno je rješenje
Napomena: ako crtate ovu krivulju u geogebri možete koordinate osi postaviti u omjer