Matematika 3 - 5.4 Graf i svojstva funkcije kotangens

Grafičko prikazivanje funkcije kotangens pomoću brojevne kružnice

Istražimo

Preslikajmo točke s brojevne kružnice u koordinatni sustav. Na os apscise nanosimo $t,$ a ordinata je $ctg t .$ Dobit ćemo grafički prikaz funkcije $f (t) = ctg t .$

Pomičite točku po kružnici i pogledajte graf koji nastaje.

Budući da je temeljni period funkcije kotangens $π,$ graf možemo proširiti na cijeli skup $R$ nanoseći ("kopirajući") osnovnu granu funkcije u beskonačnost.

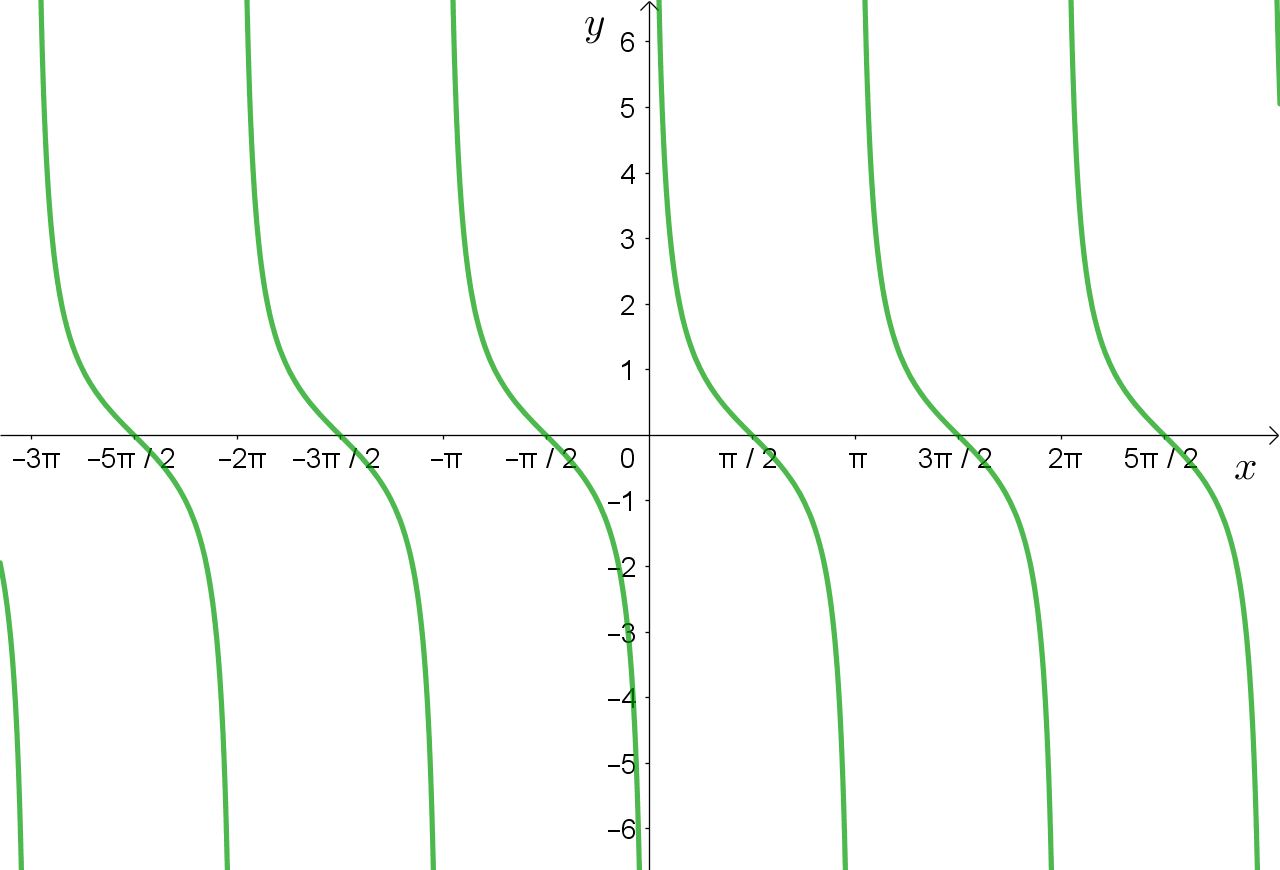
Graf funkcije kotangens je skup točaka u ravnini $Γ_{f} = \{(x, f (x)) : f (x) = ctg x, x \in R, x \neq k π, k \in Z\} .$ Graf funkcije kotangens nazivamo kotangensoida.

Grafičko prikazivanje funkcije kotangens pomoću tablice

Izračunajte vrijednosti kotangensa za realne brojeve dane u tablici.

$t$	$0$	$\frac{π}{6}$	$\frac{π}{4}$	$\frac{π}{3}$	$\frac{π}{2}$	$\frac{2}{3} π$	$\frac{3}{4} π$	$\frac{5}{6} π$	$π$
$tg t$

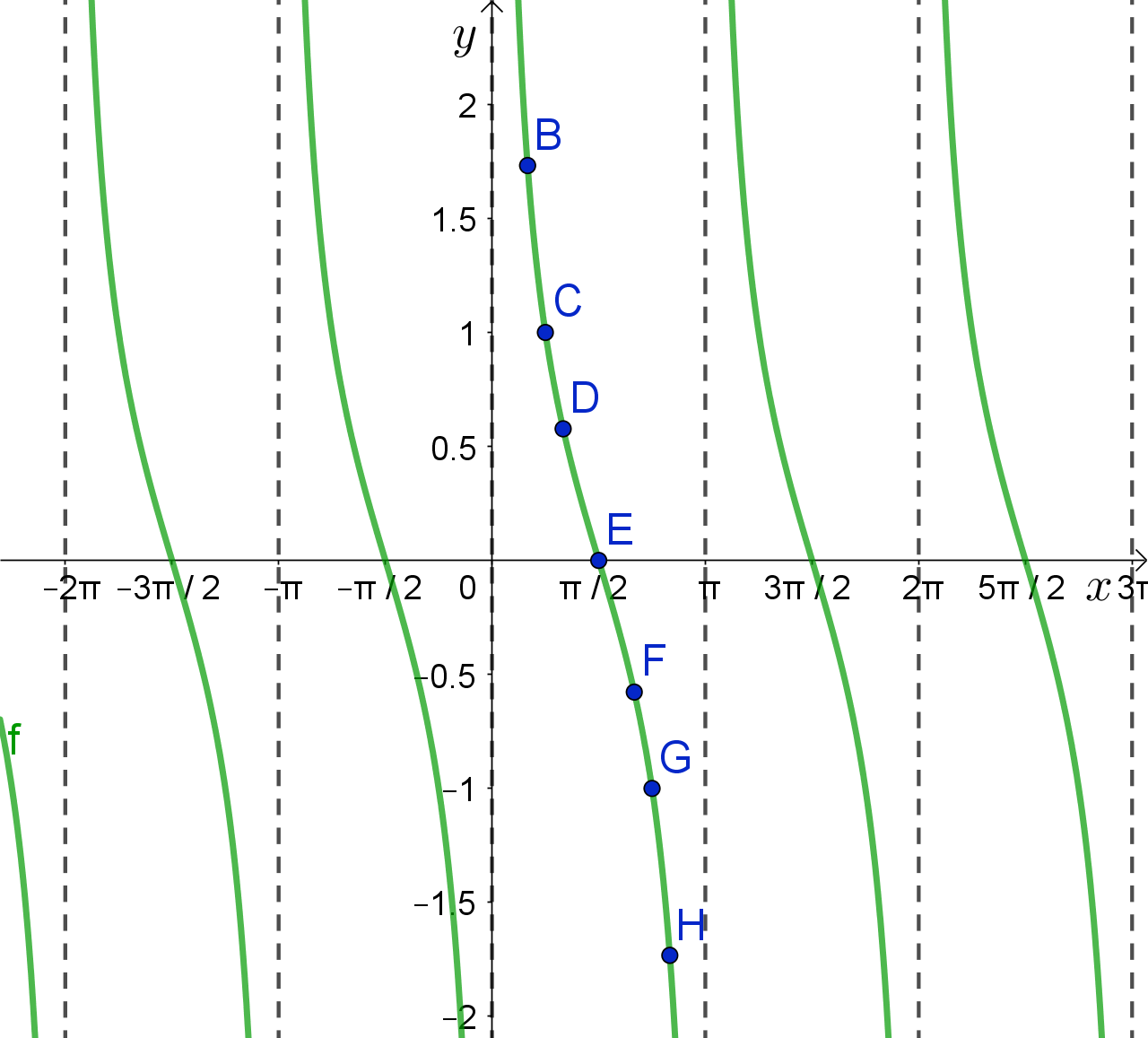
Ucrtamo li navedene točke u koordinatnom sustavu, dobit ćemo graf na intervalu $[0, π]$ koji, zbog periodičnosti, možemo proširiti na cijeli skup $R .$ Na grafu možemo uočiti i neparnost. Graf funkcije kotangens je centralnosimetričan s obzirom na ishodište.

Graf funkcije kotangens-crtanje pomoću točaka — Crtanje grafa funkcije kotangens pomoću točaka

Grafičko prikazivanje funkcije kotangens pomoću tangensa

Istražimo

Pomičite točku $T$ i pratite vrijednosti tangensa i kotangensa broja $t$ i kuta $α .$

Koje su veze između tangensa i kotangensa broja istinite?

ctg t = \frac{1}{tg t}

ctg t = tg (\frac{π}{2} + t)

{ctg}^{2} t = 1 - {tg}^{2} t

ctg t = - tg (t + \frac{π}{2})

null

Formula redukcije za kotangens glasi:

$ctg x = - tg (x + \frac{π}{2})$ za svaki $x \in R \ \{k π, k \in Z\} .$

Da bismo nacrtali graf funkcije kotangens, možemo krenuti od grafa funkcije tangens i provesti nekoliko transformacija.

Graf funkcije $f_{1} (x) = tg (x + \frac{π}{2})$ dobijemo iz grafa funkcije $f (x) = tg x$ pomakom za

lijevo

\frac{π}{2}

null

Graf funkcije $f_{2} (x) = - tg (x + \frac{π}{2})$ dobijemo iz grafa funkcije $f_{1} (x) = tg (x + \frac{π}{2})$

s obzirom na

zrcaljenjem

x

null

Svojstva funkcije kotangens

Čemu je jednak $ctg x ?$

\frac{\sin x}{\cos x}

\frac{\cos x}{\sin x}

null

Kako je $ctg x = \frac{\cos x}{\sin x}$ za svaki realan broj $x,$ pogledajmo što ćemo dobiti izjednačimo li brojnik odnosno nazivnik s nulom.

Izjednačimo li brojnik s nulom dobit ćemo nultočke funkcije kotangens.

$\cos x = 0$ daje $x = \frac{π}{2}$ ili $x = \frac{3}{2} π,$ a zbog periodičnosti i parnosti kosinusa dobivamo da su nultočke funkcije kotangens $x = \frac{π}{2} + k π$ za $k \in Z .$

Kada bi nazivnik bio $0,$ imali bismo $\sin x = 0 .$ To je ispunjeno za $x = k π$ za $k \in Z .$ U tim točkama kotangens nije definiran.

Pravce $x = k π$ za $k \in Z$ nazivamo vertikalnim asimptotama funkcije kotangens.

Istražimo

Pogledajmo kako se mijenjaju vrijednosti kotangensa kada pomičemo točku po kružnici.

Mijenjajte broj $t$ od $0$ do $π$ pa odgovorite na pitanja.

Funkcija kotangens je

intervalu od

[0, π] .

Funkcija je

stoga

je centralnosimetrična s obzirom na ishodište. Zbog svojstva

graf

funkcije "ponavlja" se u intervalima širine

π .

null

Graf funkcije kotangens ima sljedeća svojstva:

Funkcija je periodična s temeljnim periodom $π .$

Nultočke funkcije su $x = \frac{π}{2} + k π$ za $k \in Z .$

Graf funkcije kotangens ne poprima ni minimum ni maksimum.

Zbog svojstva neparnosti kotangensoida je centralnosimetrična s obzirom na ishodište.

Vertikalne asimptote su pravci $x = k π$ za $k \in Z .$

Graf funkcije pada na intervalima $⟨k π, π + k π⟩,$ $k \in Z .$

Zanimljivost

Funkcija kotangens može se prikazati pomoću Taylorovog reda:

$ctg x = \frac{1}{x} - \frac{1}{3} x - \frac{1}{45} x^{3} - \frac{2}{945} x^{5} - \frac{1}{4 725} x^{7} + . . .$ za $|x| < π .$

...i na kraju

Ponovimo što smo naučili o funkcijama tangens i kotangens.

Razvrstajte svojstva funkcija tangens i kotangens u dvije skupine: ona koja su ista za obje funkcije i ona u kojima se te dvije funkcije razlikuju

slika funkcije

Ista svojstva

Različita svojstva

null

Slika za obje funkcije je skup

, obje funkcije su

i temeljni period im je

R

neparne

π

null

Za svaki $k \in Z$ domena funkcije tangens je

, dok je domena funkcije kotangens

R \ \{\frac{π}{2} + k π\}

R \ \{k π\}

null

Nultočke funkcije tangens su

, a funkcije kotangens

za svaki

k \in Z

\frac{π}{2} + k π

k π

null

Vertikalne asimptote funkcije tangens su

, a funkcije kotangens su

za svaki

k \in Z

x = k π

x = \frac{π}{2} + k π

null

Funkcija tangens je

između dviju vertikalnih asimptota, a funkcija kotangens je

između dviju vertikalnih asimptota.

rastuća

padajuća

null

Na početku...

Grafičko prikazivanje funkcije kotangens pomoću brojevne kružnice

Istražimo

Grafičko prikazivanje funkcije kotangens pomoću tablice

Grafičko prikazivanje funkcije kotangens pomoću tangensa

Istražimo

Svojstva funkcije kotangens

Istražimo

Zanimljivost

...i na kraju

Ista svojstva

Različita svojstva