Matematika 3 - Aktivnosti za samostalno učenje

Na početku...

Periodičnost je svojstvo koje se može uočiti u puno pojava u svijetu koji nas okružuje.

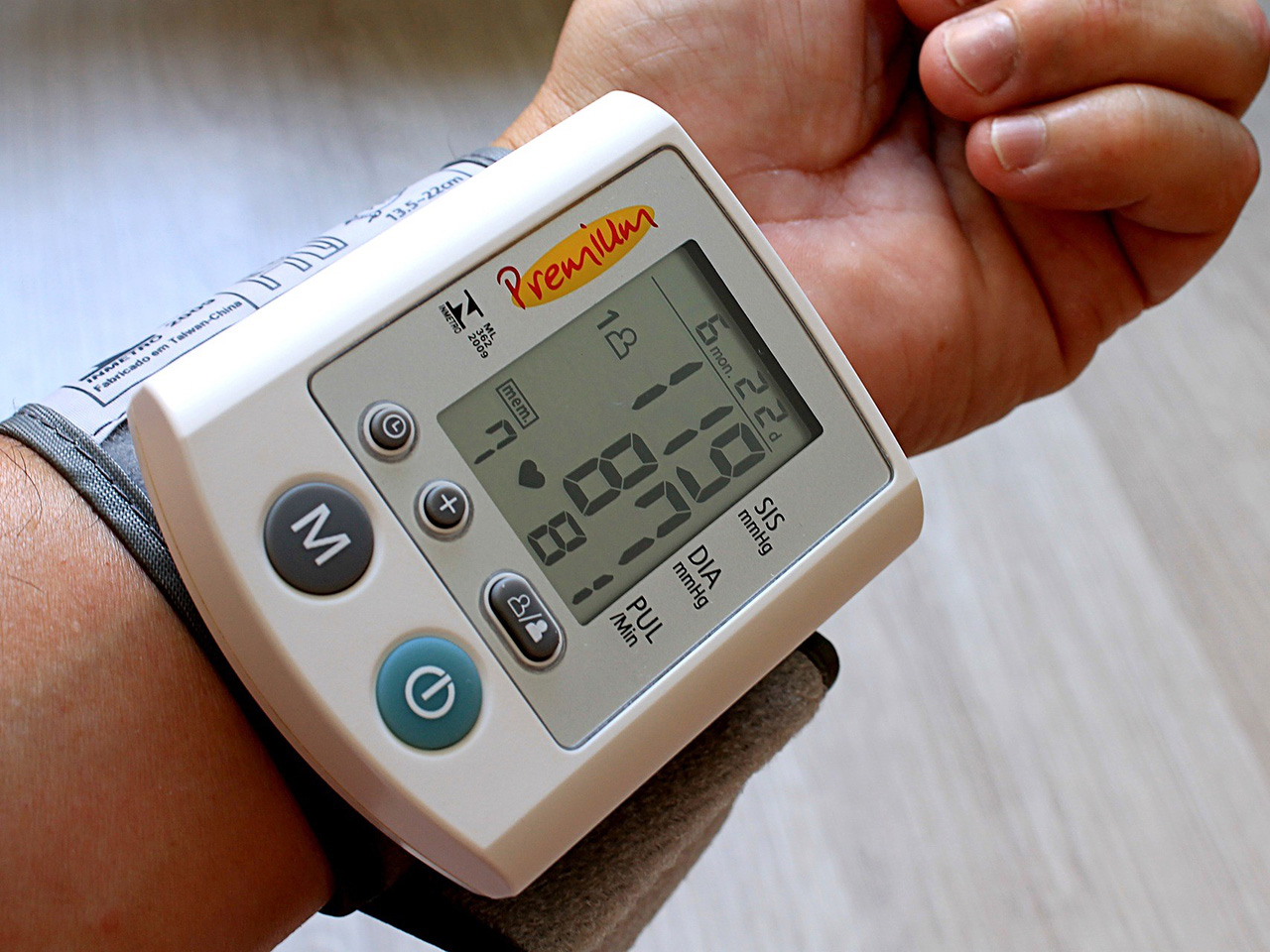
Jeste li dosada mjerili krvni tlak? Znate li što predstavljaju brojke koje dobijete kao rezultat mjerenja tlaka? Osim tlaka, možemo očitati i puls, odnosno broj otkucaja srca u jednoj minuti. To su tri podatka koje možete pročitati i na digitalnom tlakomjeru ove fotografije.

Mjerenje pulsa kažiprstom — Mjerenje pulsa

Zanimljivost

Krvni tlak ovisi o snazi srca koje pumpa krv u tijelo i o širini arterija. Optimalan krvni tlak je do $120 / 80 mgHg .$ Prvi broj predstavlja gornji ili sistolički tlak koji se dobije kada srce izbacuje krv u arterije. Drugi broj predstavlja donji ili dijastolički tlak kada se srce opušta da bi krv primilo.

Puls je ritmičko širenje arterija (žile kucavice). Normalan puls je između 60 i 100 otkucaja u minuti. Znate li kako možete izmjeriti puls opipavanjem na zapešću ili vratu?

Frekvencija ili period?

Ponovite!

Vremenski interval nakon kojeg se vrijednost, odnosno graf funkcije ponavlja je

. Broj ponavljanja istog oblika krivulje u jedinici vremena je

period

frekvencija

null

U kojem međusobnom odnosu su period i frekvencija?

Proporcionalne su

Obrnuto su proporcionalne

Jednakih su mjera

Neusporedive su

null

Koje su mjerne jedinice danih veličina?

Period
Frekvencija

null

Zadatak 1.

Krvni tlak prosječne osobe može se modelirati periodičnom funkcijom $p (t) = 20 \sin (160 π t) + 100$ gdje je $t$ vrijeme u sekundama. Nacrtajte graf ove funkcije. Možete li zaključiti koliko se puta "jedan val" sinusoide ponavlja unutar jedne sekunde?

Uočite odnos veličina $t$ i $p (t)$ i u skladu s tim, označite koordinatne osi (npr. u omjeru $x : y = 1 : 1 000$ ).

Amplituda, $A = 20 .$

Vertikalni pomak, $d = 100 .$

Faznog pomaka nema.

Period je $\frac{2 π}{160 π} = \frac{1}{80}$ pa je frekvencija $80 .$

Sinusoida krvnog tlaka. — Sinusoida tlaka

Interpretirajmo dobivene podatke. Kako ih možemo povezati s krvnim tlakom i pulsom?

Pridružite pripadajuće vrijednosti izračunatim veličinama funkcije $p (x) .$

Maksimum
Minimum
Period
Frekvencija

null

Povežite dobivene iznose s vrijednostima krvnog tlaka.

Temeljni period	Jedan otkucaj srca
Minimum	Sistolički tlak
Maksimum	Diijastolički tlak
Frekvencija	Puls

null

Zadatak 2.

Pogledajte sljedeći video.

Projekt

Pomoću videa modelirajte ovo skakanje tako da se dobivenom funkcijom može izračunati udaljenost od poda u ovisnosti o vremenu.

Uputa:

Izmjerite/procijenite najvišu udaljenost od poda (maksimum). Koliki je minimum?
Izmjerite vrijeme potrebno za jedan skok (period).
Koliko je skokova u jednoj sekundi, odnosno koliki dio skoka traje jednu sekundu (frekvencija)?

Modeliranje digitalnim alatima

Odredite funkciju skakanja u zrak pomoću sljedeće interakcije. Za određivanje sinusoide potrebni su nam sljedeći elementi: amplituda (minimum/maksimum ili prosječna vrijednost), period (vrijeme potrebno za jedan skok) i, kada to smjestimo u koordinatni sustav, pomak po osi ordinate.

Zadatak 3.

Iskoristite prethodni predložak za modeliranje preskakanja vijače. Na slici vidite vijaču u položaju kada je najudaljenija od poda. Pronađite način kako odrediti tu maksimalnu visinu. Ako jedan krug koji vijača prođe traje 3/4 sekunde, modelirajte to gibanje.

Istražimo

Najprije procijenite kolika je visina osobe koja preskače vijaču. Nakon toga, izmjerite i koristeći proporcije utvrdite maksimalnu visinu vijače.

Uvijek možete upotrijebiti i svoju visinu za rješavanje zadatka. Ne samo visinu, nego doista preskačite vijaču i izmjerite sve potrebne podatke. Možete zamoliti profesoricu na tjelesnom odgoju da vam pomogne u tome.

Nakon prikupljenih podataka, izračunajte preostale podatke potrebne za određivanje sinusoide. Kao pomoć može vam poslužiti ova fotografija smještena u koordinatni sustav.

Osoba s vijačom smještena u koordinatni sustav. — Vijača u koordinatnom sustavu

Uočimo: $visina osobe : 6 = visina vijače : 7.1 .$

Što predstavlja podatak $3 / 4$ sekunde?

To je frekvencija iz koje lako dobijete temeljni period.

Odnos centimetra i inča na primjeru metra

Zanimljivost

Stopa (eng. foot) je angloamerička mjera za duljinu. Oznaka za stopu je $ft .$ Angloamerički sustav mjera uglavnom se koristi u SAD-u i Velikoj Britaniji gdje vrijedi $1 ft = 0.3048 m .$

Neke od ostalih mjernih jedinica za duljinu su palac (inč ili col) i jard $(1 yd = 3 ft = 12 in) .$ Već otprije vam je poznato da je $1 in = 2.54 cm .$

Kolekcija zadataka #1

Funkcijom $h (t) = 4 \cos (\frac{π}{6} t) + 11$ dana je razina mora u jednom američkom gradiću u vremenu od ponoći do podneva gdje je $t$ vrijeme u satima, a $h (t)$ razina mora u stopama. U koje vrijeme će biti oseka, a u koje plima? Kolika je razina mora za vrijeme plime, a kolika za vrijeme oseke? Skicirajte sinusoidu.

Kako biste mogli koristiti prethodnu interakciju za provjeru rješenja, najprije prevedite funkciju kosinus u funkciju sinus pomoću formule redukcije: $\cos t = \sin (t + \frac{π}{2})$ $\Rightarrow h (t) = 4 \sin (\frac{π}{6} t + \frac{π}{2}) + 11 .$

$\cos (\frac{π}{6} t) = \sin (\frac{π}{6} t + \frac{π}{2}) = \sin (\frac{π}{6} (t + 3)) \Rightarrow$ pomak sinusoide je po osi apscisa za 3 ulijevo.

Rješenje na slici dobiveno je pomoću prethodne interakcije.

Grafički prikaz rješenja zadatka 1. — Rješenje zadatka 1

Za funkciju $f (x) = 5 \sin (π t)$ odredite ekstreme, temeljni period, frekvenciju i skicirajte graf. Kada će funkcija poprimiti vrijednost $0 ?$

Uz pomoć prethodne interakcije lako možete provjeriti jeste li dobili točan rezultat. Nakon crtanja grafa, dobivena jednadžba mora se slagati sa zadanom.

Grafički prikaz rješenja zadatka 2. — Rješenje zadatka 2

Funkcija poprima vrijednost $0$ za sve $x \in Z .$

Nacrtajte sinusoidu $y = 2 \sin (4 x - \frac{π}{2}) + 2 .$ Odredite nultočke funkcije.

Grafički prikaz rješenja zadatka 3. — Rješenje zadatka 3

Nultočke: $\{(k \cdot \frac{π}{2}, 0) : k \in Z\}$

...i na kraju

Za kraj, uz pomoć GGB nacrtajte i analizirajte sljedeću funkciju: $f (x) = - \frac{1}{2} tg (x - \frac{π}{4}) .$ Odredite intervale na kojima je funkcija definirana i nultočke funkcije. Je li funkcija rastuća?

Na isti način možete u polje za unos upisati i, potom, analizirati proizvoljnu trigonometrijsku funkciju.

Funkcija nije definirana za $x_{k} = - \frac{π}{4} + k \cdot π,$ $k \in Z .$

Nultočke su $(\frac{π}{4} + k \cdot π, 0),$ $k \in Z$

Funkcija pada i intervali pada funkcije su: $⟨- \frac{π}{4} + k \cdot π, - \frac{π}{4} + (k + 1) \cdot π⟩,$ $k \in Z$