


Zašto vodene biljke i životinje preživljavaju zimu i niske temperature?
Primjer 1.
Eksperimentalnim je putem dobiveno da će količina vode, koja na zauzima obujam od jedne litre, na temperaturi imati obujam od litara, za temperature iz intervala
Gustoća vode je maksimalna kada je obujam minimalan. Odredimo na kojoj će se temperaturi to dogoditi.
Kako bismo odredili kad funkcija postiže minimalnu vrijednost, prvo moramo odrediti njezine stacionarne točke.
Na zadanoj domeni stacionarna je točka
Uparite
s pripadajućim iznosom:
|
|
|
|
|
|
|
|
Uočimo da je i Tablica tijeka funkcije za je:
Lokalni minimum funkcija postiže u točki Prema tome zaključujemo da je minimalna vrijednost obujma vode na temperaturi od
Je li vas ovaj odgovor iznenadio?
Voda je jedina tekućina čija je najveća gustoća iznad točke ledišta (kod vode
).
Kod hlađenja ispod voda se, za razliku od drugih tvari, rasteže. Ovo se nepravilno rastezanje zove anomalija vode i igra važnu ulogu u prirodi. U hladnim zemljama, zimi, kada je atmosferska temperatura vrlo niska, gornji se slojevi vode u jezerima i ribnjacima počinju hladiti. Kad temperatura površinskog sloja padne na voda postiže maksimalnu gustoću i tone. Donji slojevi vode tada se uzdižu. Ova se voda također hladi na i ponovno tone. Proces se nastavlja sve dok temperatura cijele vode ne padne na Kako temperatura pada ispod gustoća vode opada i kao rezultat toga voda na površini postaje svjetlija i ne tone. Površinska voda se konačno smrzava, dok donji slojevi ostaju na Tako ispod smrznutog sloja preživljavaju vodene životinje i biljke.
Uočite da funkcija
ima za
ne samo lokalni minimum, već i minimum na cijeloj svojoj domeni, intervalu
Još kažemo da je
globalni minimum funkcije
U mnogim praktičnim problemima tražimo najveću i najmanju vrijednost neprekidne funkcije na nekom intervalu, takozvani globalni maksimum i globalni minimum. Na tomu intervalu funkcija može imati više lokalnih ekstrema, a može se dogoditi i da je najmanja vrijednost funkcije lokalni minimum ili pak vrijednost funkcije u nekoj od rubnih točaka. Primjerice, kao na sljedećoj ilustraciji. Također i najveća vrijednost funkcije može biti lokalni maksimum ili vrijednost funkcije u nekoj od rubnih točaka.
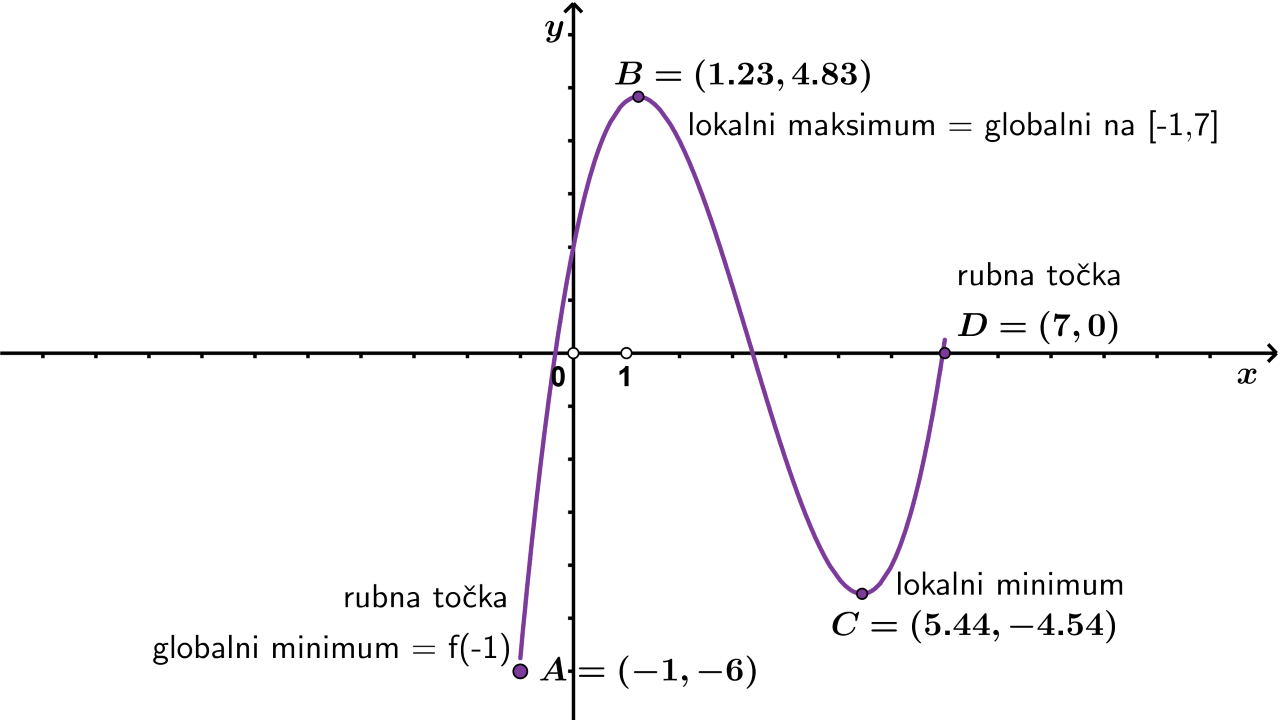
Funkcija koja je neprekidna na zatvorenom intervalu postiže najveću i najmanju vrijednost u točkama lokalnih ekstrema ili u rubnim točkama, odnosno Najmanja, odnosno najveća vrijednost od brojeva i lokalnih ekstrema je ujedno i najmanja, odnosno najveća vrijednost funkcije na zadanom intervalu.
Mjerenjem protočnosti prometa u razdoblju od do na cesti kojom se izlazi iz grada, ustanovljeno je da se brzina odvijanja prometa može opisati funkcijom gdje je broj sati nakon a brzina prometa u
U kojem se trenutku, u promatranom razdoblju, promet odvija najbrže, a u kojem najsporije?
Tražimo najveću i najmanju vrijednost funkcije
na intervalu
na kojem se mjeri vrijeme proteklo od 12:00 do 18:00.
Prvo odredimo derivaciju zadane funkcije i stacionarne točke.
pa su stacionarne točke
Vrijednost funkcije u stacionarnim točkama je a vrijednost funkcije u rubnim točkama intervala je
Kako je
na
a
na intervalima
broj
je lokalni maksimum, a broj
lokalni minimum.
No, najveća vrijednost funkcije na zadanom intervalu iznosi
a najmanja
(Uočite da se najveća vrijednost
postiže u rubnoj točki, a ne u točki lokalnog maksimuma.)
To znači da se promet odvija najbrže u
a najsporije u
Prema istraživanju Tuckera i Schmidt-Koeniga (Flight Speeds of Birds in Relation to Energetics and Wind directions, The Auk, Vol. 88 1971., str. 97–107) energija koju troši jedna vrsta australske papige pri letu ovisi o njezinoj brzini leta i može se aproksimirati s:
gdje je
brzina papige u
Koja će brzina minimizirati potrošnju energije?
Poredajte korake u rješavanju zadatka.
U dizajniranju zrakoplova važnu ulogu ima otpor, odnosno sila usporavanja kojom zrak djeluje na zrakoplov. Jedan model kojim se mjeri otpor dan je funkcijom
gdje su
i
pozitivne konstante, a
brzina zrakoplova u
Eksperimentalno je utvrđeno da je otpor minimalan pri brzini od
Odredite omjer
Slijedi
Kako je
točka minimuma, ona je i stacionarna točka, pa zadovoljava jednadžbu
odnosno
što je ujedno i traženi omjer.
Količina vode (u litrama) koja se nalazi u spremniku sati nakon početka punjenja dana je formulom Voda se iz spremnika može istovremeno i trošiti.
Kako izgleda graf funkcije
od trenutka kad se spremnik počeo puniti do trenutka kad se ispraznio?
Odgovori na sljedeća pitanja pomoći će vam da dođete do rješenja.
Koristeći se dobivenim podatcima skicirajte graf funkcije
U prethodnim smo zadatcima primijenili derivaciju i njezina svojstva kako bismo odredili minimum ili maksimum funkcije kojom se modelira neka situacija. No, ta je funkcija bila unaprijed zadana. U praksi to obično nije tako jednostavno i treba prvo prikupiti sve korisne podatke, zatim formulirati model i nakon toga minimizirati ili maksimizirati, odnosno optimizirati funkciju koja ga opisuje.
Primjer 2.
Parabola je zadana jednadžbom Odredimo dimenzije najvećeg pravokutnika koji se može upisati u parabolu tako da su mu dva vrha na osi
Pomicanjem točke u interakciji mijenja se površina pravokutnika. Promatrajte što se događa i odgovorite na pitanja koja slijede.

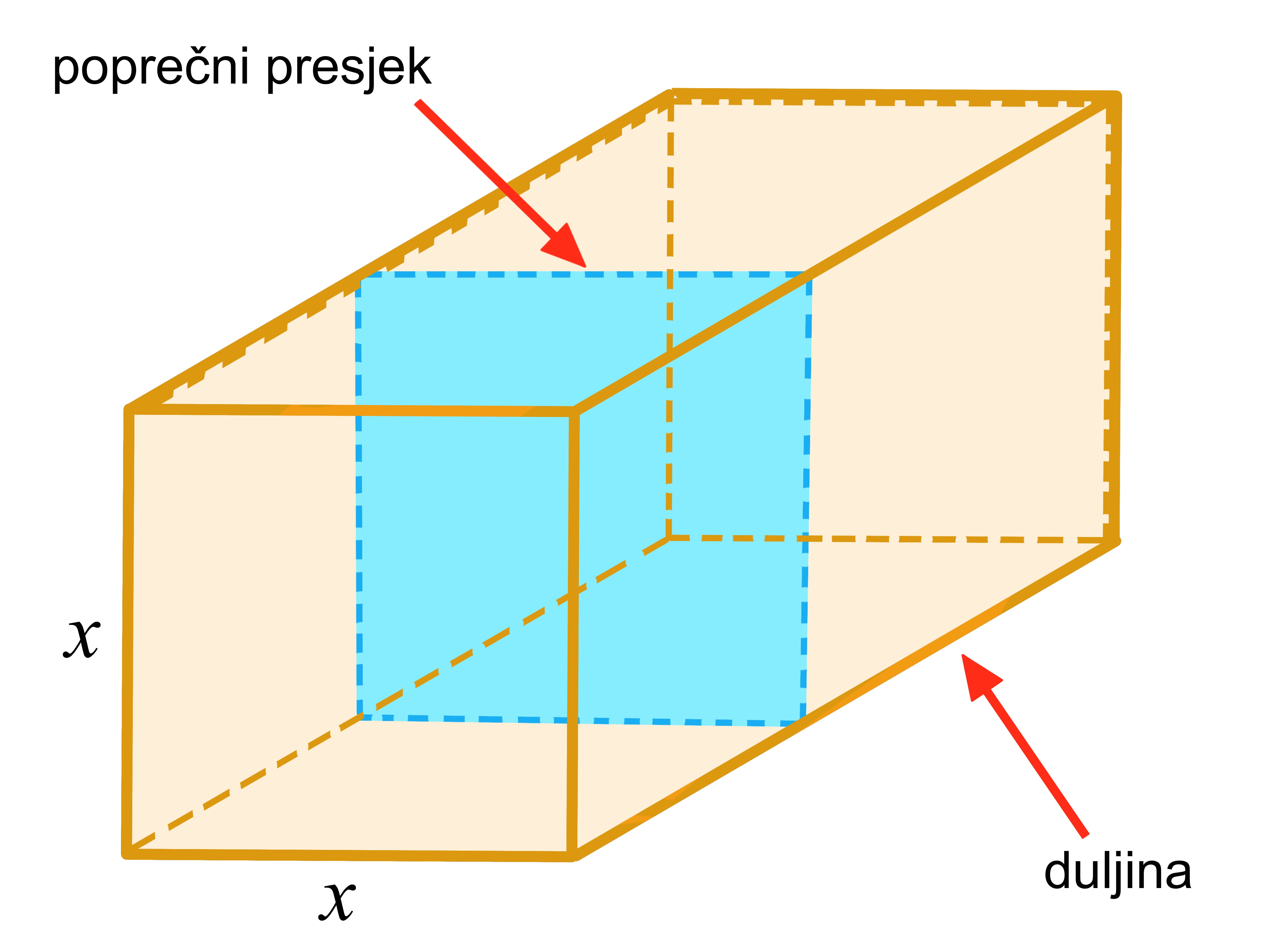
Dimenzije i masa paketa koji se šalje poštom određene su poštanskim propisima. Tako za dimenzije vrijedi da zbroj duljine i opsega poprečnog presjeka (na najširem dijelu) paketa može iznositi do
s tim da najveća dimenzija paketa može iznositi do
Koliko iznosi obujam najvećeg paketa koji možete poslati u obliku kvadra kao na slici?
Poredajte korake prema redoslijedu rješavanja.
Ako je
duljina stranice kvadratne baze, a
duljina paketa, poprečni je presjek također kvadrat duljine stranice
i prema zadanom propisu vrijedi
i možemo pisati:
Pomoć:
u
ima maksimum jer na intervalu
ima predznak plus, a na intervalu
predznak minus. Dakle, do
funkcija
raste, a zatim pada. Nulište prve derivacije je i točka
ali nije u domeni funkcije.
Postupak:
Iz veze
vidimo da je
Uz podatke iz prethodnog zadatka, koliko iznosi obujam najvećeg paketa koji možete poslati u obliku valjka?
Najveći je obujam
Primjer 3.
Limar je dobio narudžbu da od komada lima pravokutnog oblika, dimenzija napravi otvorenu kutiju maksimalnog obujma.
U sljedećoj interakciji mijenjajte položaj točke označene na tlocrtu kutije i promatrajte što se događa s kutijom, odnosno njezinim obujmom. Procijenite za koju će vrijednost odrezanog kvadratića kutija imati maksimalni obujam i koliko on iznosi. Svoju procjenu provjerite računski s pomoću sljedećih pitanja.
Riješite prethodni zadatak i općenito, odnosno odredite koji će maksimalni obujam imati otvorena kutija koju treba napraviti od pravokutnog lima (ili kartona) duljina stranica
Maksimalni obujam dobit će se za
Kako nije mogla naći kutiju odgovarajućih dimenzija, Ana je odlučila sama napraviti kutiju. Njezina kutija treba biti zatvorena (imati poklopac), imati kvadratnu bazu i obujam od
Materijal za dno i vrh kutije stoji
a za bočne strane
Može li se kutija napraviti za manje od
kuna? Koje će dimenzije imati najjeftinija kutija?
Cijena izrade kutije jednaka je
a ova funkcija ima minimalnu vrijednost
za
To znači da se kutija ne može izraditi za
kuna ili manje.
Najjeftinija kutija ima dimenzije
Kamion se nalazi
istočno od automobila i kreće se prema zapadu konstantnom brzinom od
Istovremeno se automobil kreće prema sjeveru konstantnom brzinom od
Kada će kamion i automobil biti najbliže? Koliko iznosi ta minimalna udaljenost kamiona i automobila?
Pogledajte rješenje zadatka u sljedećem videozapisu.