Definirajmo pravilo koje svakome danu u godini pridružuje jedno od četiriju godišnjih doba.
Je li takvo pridruživanje funkcija? Što je domena, a što slika funkcije? Nacrtajte graf.
Takvo pridruživanje jest funkcija jer svakome danu u godini pridružuje samo jedno godišnje doba.
Domena funkcije su dani u godini počevši, primjerice, od 1. 1. 2019. godine, a slika funkcije skup {proljeće, ljeto, jesen, zima}.
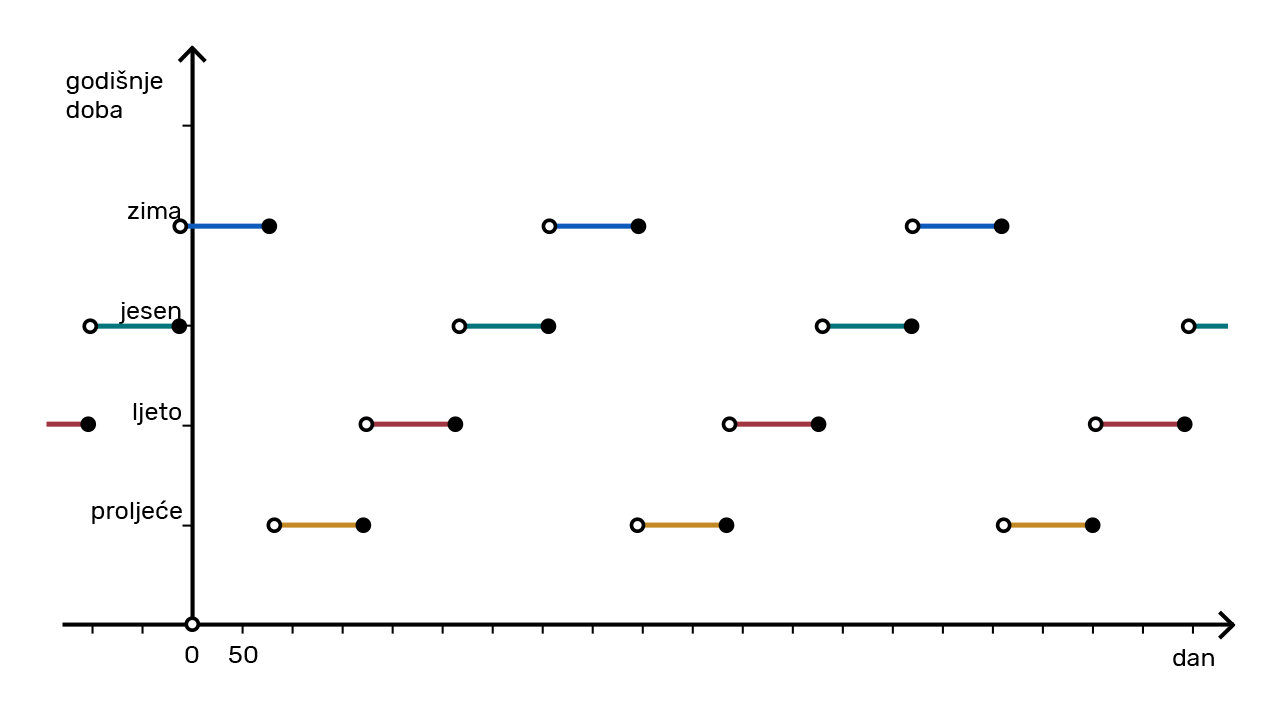
Što znamo o godišnjim dobima tijekom jedne godine? A što tijekom više godina?
Tijekom jedne godine godišnja se doba redom izmijene, a tijekom više godina ponavlja se isti slijed.
Za funkciju f kažemo da je periodična s periodom T>0 ako je za svaki x iz domene funkcije f i x+T u domeni i vrijedi f(x+T)=f(x).
Najmanji broj
T (ako postoji) zove se temeljni period funkcije
f.
Pogledajmo sada uvodni primjer.
Godišnja doba imaju uvijek isti slijed i isto trajanje. Možemo reći da je funkcija periodična.
Koliki je period?
12 mjeseci ili 365 dana, uz pretpostavku da smo zanemarili prijestupne godine.
Promotrite elementarne funkcije:
f(x)=|x|,
g(x)=√x,
h(x)=1x,
i(x)=ax,
j(x)=logax,
k(x)=sinx,
l(x)=cosx,
m(x)=tgx. Ima li među njima periodičnih? Ako da, koliki im je temeljni period?
Periodične su
k(x)=sinx,
l(x)=cosx,
m(x)=tgx
. Temeljni period funkcija
k(x)=sinx i
l(x)=cosx je
2π, a funkcije
m(x)=tgx
je
π.
Primjer 1.
Odredimo temeljni period funkcije f(x)=sin(ax).
Budući da je ova funkcija definirana za sve realne brojeve, onda je zasigurno zadovoljen prvi uvjet iz definicije periodičnosti, tj. za svaki x je i x+T u domeni funkcije.
Mora vrijediti i da je f(x+T)=f(x). Pogledajmo.
f(x+T)=sin(a(x+T))=sin(ax+aT)
Da bi to bilo jednako f(x), odnosno sin(ax), zbog periodičnosti funkcije sinus mora biti
|aT|=2π, odnosno T=2π|a|.
Analogno možemo dokazati da je temeljni period funkcije
f(x)=cos(ax) jednak
T=2π|a|, a temeljni period funkcije
f(x)=tg(ax) jednak
T=π|a|.
Temeljni period funkcije f(x)=2cos(-23x+π) iznosi
Primjer 2.
Koliki je temeljni period funkcije f(x)=sinx2+sinx3?
Rješenje pogledajmo u sljedećem videu.
Riješite sljedeće zadatke.
Neka su
f, dvije funkcije. Ako je
periodična funkcija, dokažite da je kompozicija funkcija
periodična.
Funkcija
svakome realnom broju
pridružuje najmanji cijeli broj koji nije manji od
Tako je primjerice
.
Nacrtajmo graf funkcije
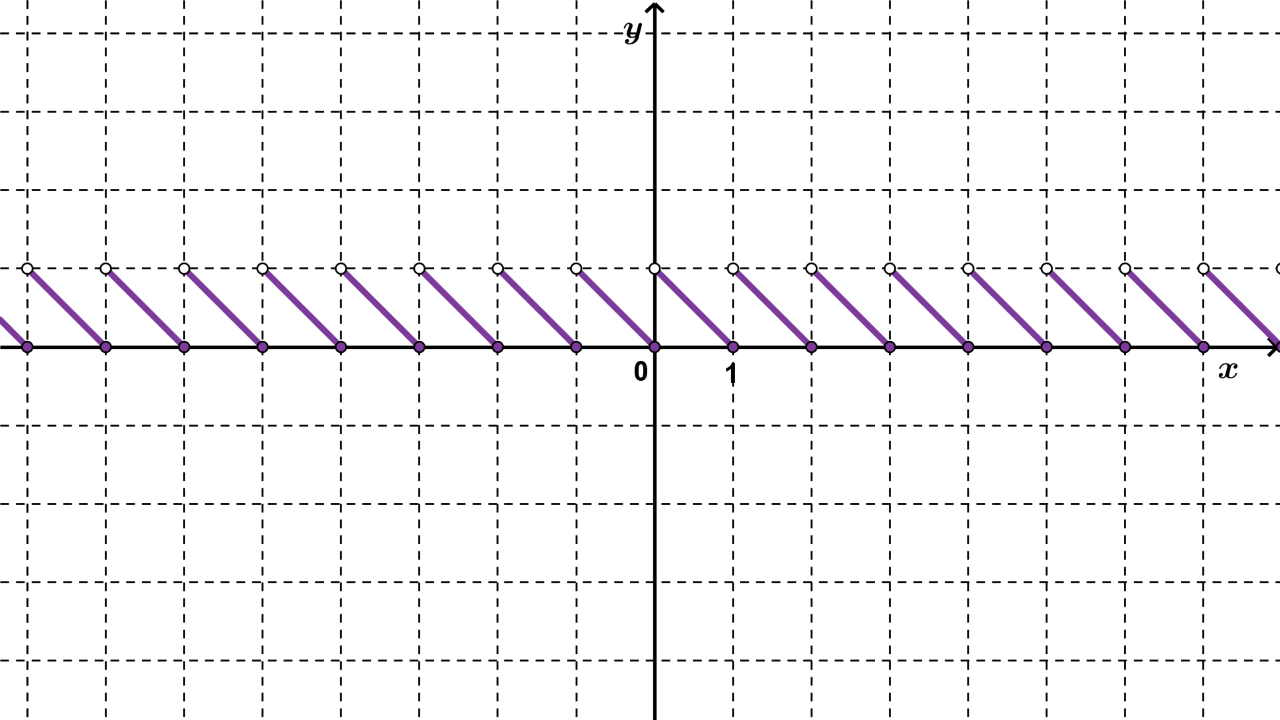
Iz grafa funkcije možemo zaključiti da je funkcija periodična.
Koliki joj je temeljni period?
Riješite sljedeće zadatke.
Je li funkcija čiji je graf prikazan na slici periodična, uz pretpostavku da se tijek funkcije ne mijenja na cijelom skupu realnih brojeva?
Ako jest, odredite joj period.
Je li funkcija čiji je graf prikazan na slici periodična, uz pretpostavku da se tijek funkcije ne mijenja na cijelom skupu realnih brojeva?
Ako jest, odredite joj period.
Je li funkcija čiji je graf prikazan na slici periodična, uz pretpostavku da se tijek funkcije ne mijenja na cijelom skupu realnih brojeva?
Ako jest, odredite joj period.
Je li funkcija čiji je graf prikazan na slici periodična, uz pretpostavku da se tijek funkcije ne mijenja na cijelom skupu realnih brojeva?
Ako jest, odredite joj period.
Koje su od sljedećih stvarnih situacija periodične?
Visina lopte (c.) nije, jer se tijekom vremena smanjuje. Ostale možemo smatrati periodičnima.
