Matematika 1 - 5.3 Polovište dužine

Formula za polovište dužine u koordinatnom sustavu

Kako to izgleda u koordinatnom sustavu.

Zadatak 1.

Neka su zadane točke $A (- 3, 2),$ $B (5, 8)$ i $P (1, 5) .$ Nacrtajte ih u koordinatnom sustavu u bilježnicu. Izračunajte $|A B|,$ $|A P|$ i $|B P| .$ Što možete zaključiti o točki $P ?$

Proučite u kojem su odnosu brojevi $- 3, 5, 1,$ tj. apscise točaka $A, B$ i $P .$ A ordinate, odnosno $2, 8, 5 ?$

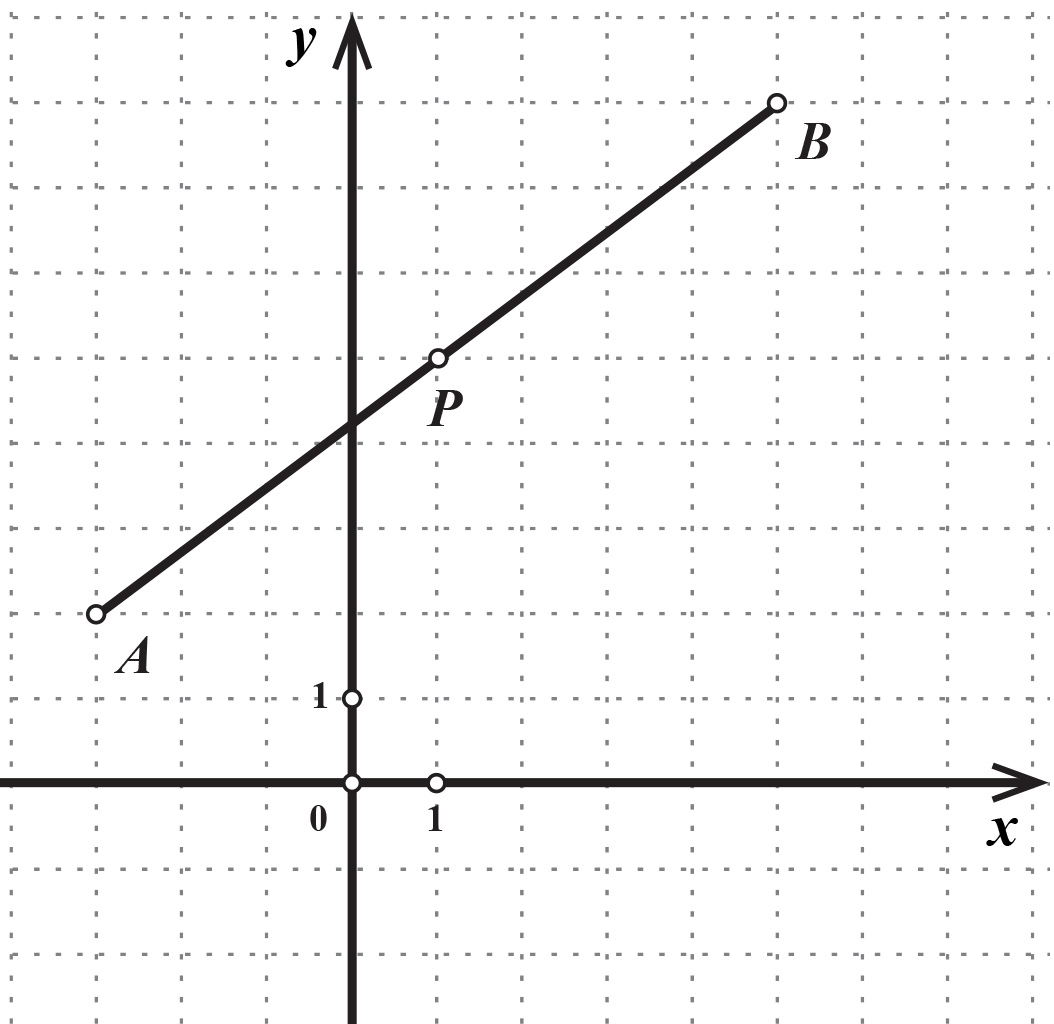
Na slici su točke A, B i P u koordinatnom sustavu.

$d (A, P) = d (B, P),$ odnosno točka $P$ polovište je dužine $\bar{A B} .$

Apscisa točke $P$ aritmetička je sredina apscisa točaka $A$ i $B .$ Isto vrijedi i za ordinate točaka.

Neka su $A (x_{1}, y_{1})$ i $B (x_{2}, y_{2})$ točke u koordinatnoj ravnini. Ako je točka $P (x_{P}, y_{P})$ polovište dužine $\bar{A B},$ tada je:

$x_{P} = \frac{x_{1} + x_{2}}{2}$ ; $y_{P} = \frac{y_{1} + y_{2}}{2} .$

Dokažimo formulu. Pogledajte skicu.

Uparite koordinate i odgovarajuće točke.

$(x_{P}, y_{P})$

$(x_{1}, y_{P})$

$(x_{P}, y_{2})$

null

null
Trokuti $A T_{1} P$ i $P T_{2} B$ su
sukladni
jer se podudaraju u svim
kutovima
i duljini jedne
stranice
, $|A P| = |B P| .$

Tada su i ostale odgovarajuće stranice
jednakih duljina
, pa je $|A T_{1}| = |P T_{2}|$ i $|T_{1} P| = |T_{2} B| .$

null

null
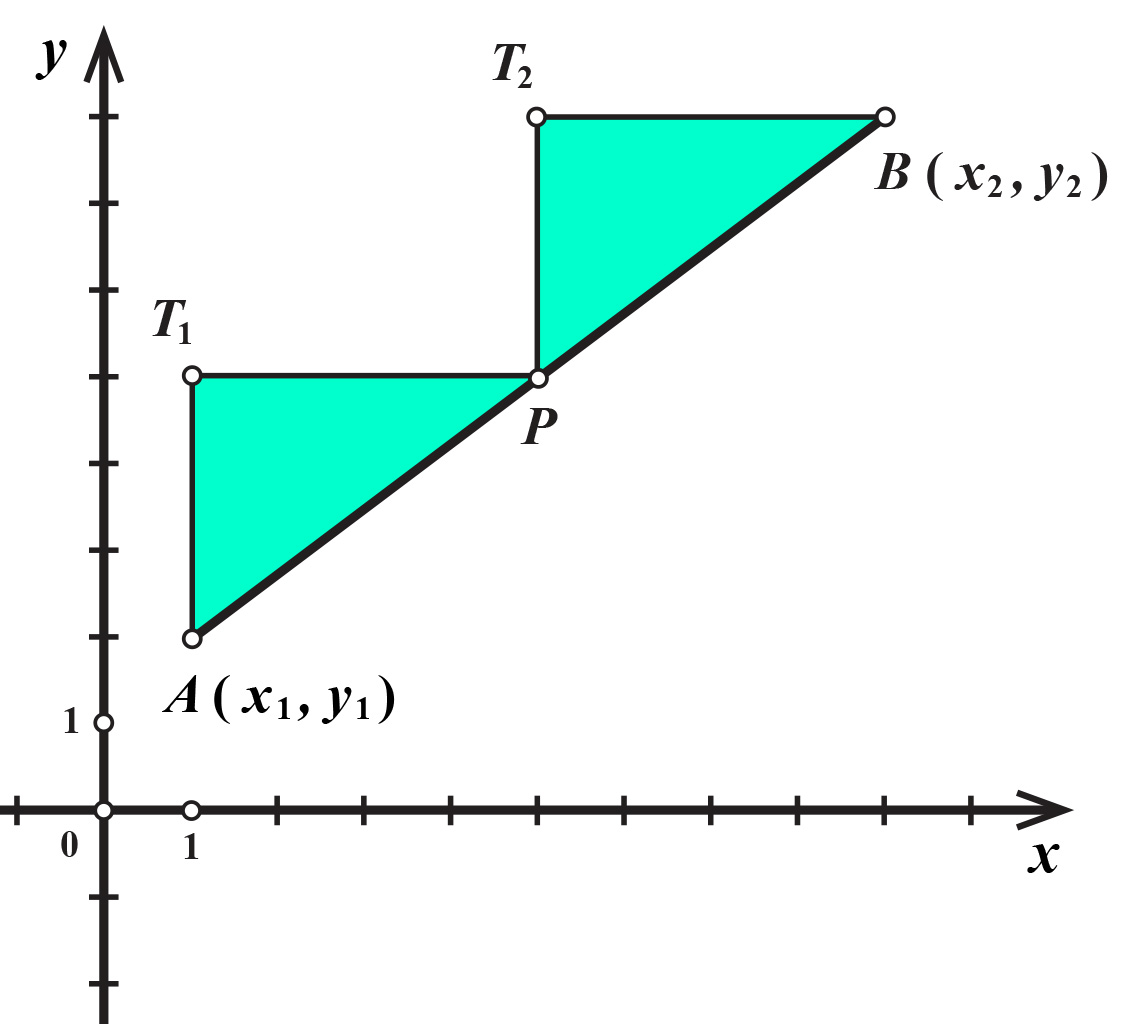
Sada je:
$x_{P} = \frac{x_{1} + x_{2}}{2}$

$2 x_{P} = x_{1} + x_{2}$

$x_{P} - x_{1} = x_{2} - x_{P}$

$|T_{1} P| = |T_{2} B|$
null

null
Nadalje,
$|A T_{1}| = |P B|$

$y_{P} = \frac{y_{1} + y_{2}}{2}$

$y_{P} - y_{1} = y_{2} - y_{P}$

$2 y_{P} = y_{1} + y_{2}$
null

null

Time smo formulu dokazali.

Grafičko određivanje polovišta dužine

Polovište dužine možemo odrediti grafički, a koordinate očitati u koordinatnom sustavu.

Kolekcija zadataka 1

Zadatak 2.

Označite polovište dužine u koordinatnom sustavu tako da kružić uz točku $P$ namjestite na mjesto polovišta. Očitajte koordinate polovišta dužine.

$P_{\circ}$

null

null
$P ($ , $)$

null

null
$P_{\circ}$

null

null
$P ($ , $)$

null

null
$P_{\circ}$

null

null
$P ($ , $)$

null

null
$P_{\circ}$

null

null
$P ($ , $)$

null

null

Zadatak 3.

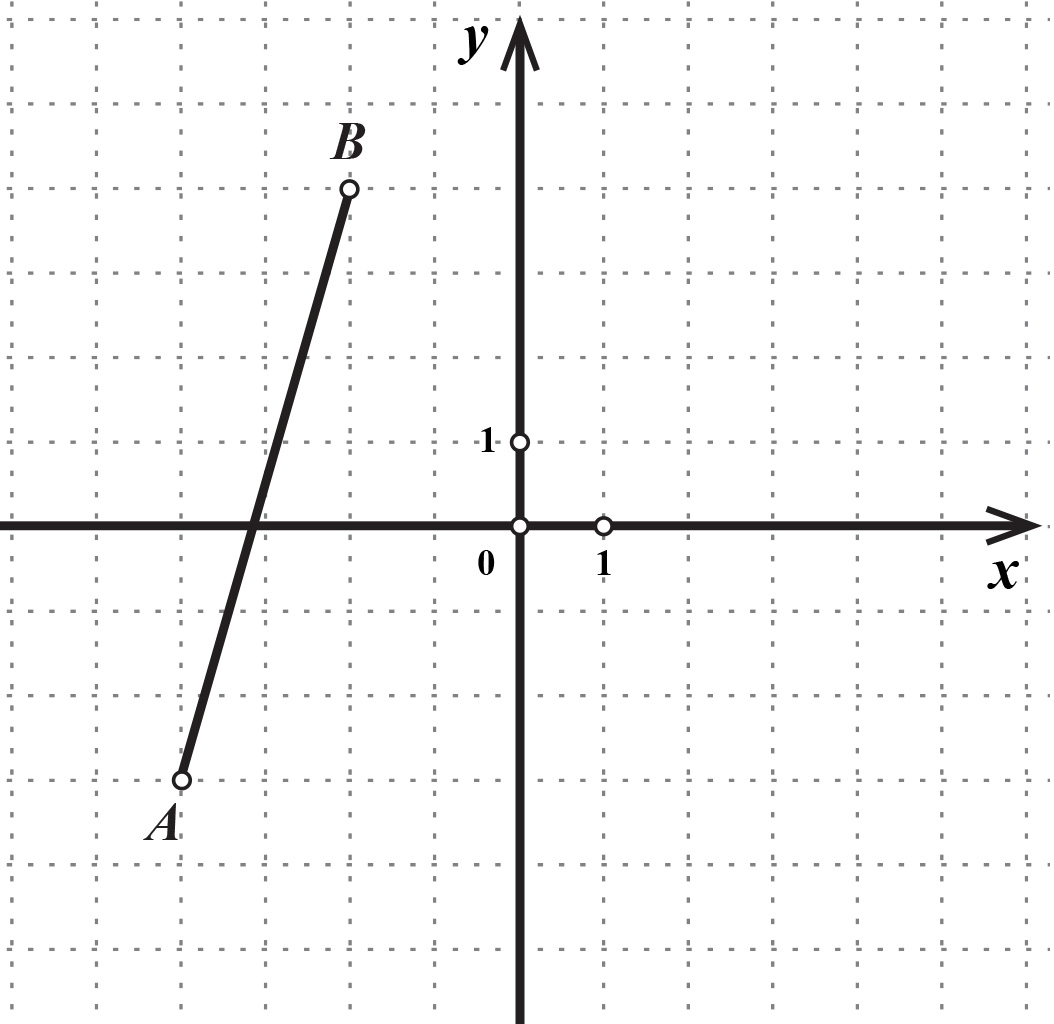
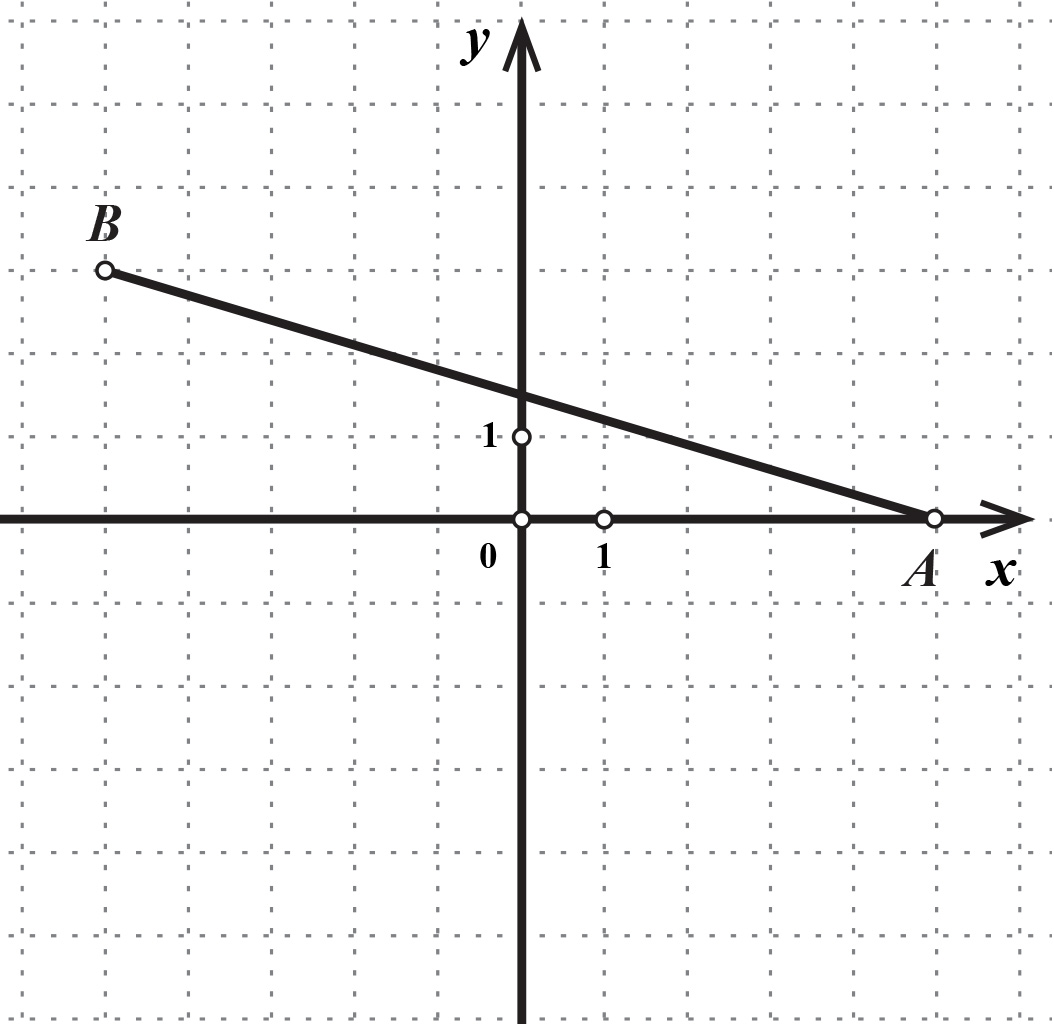
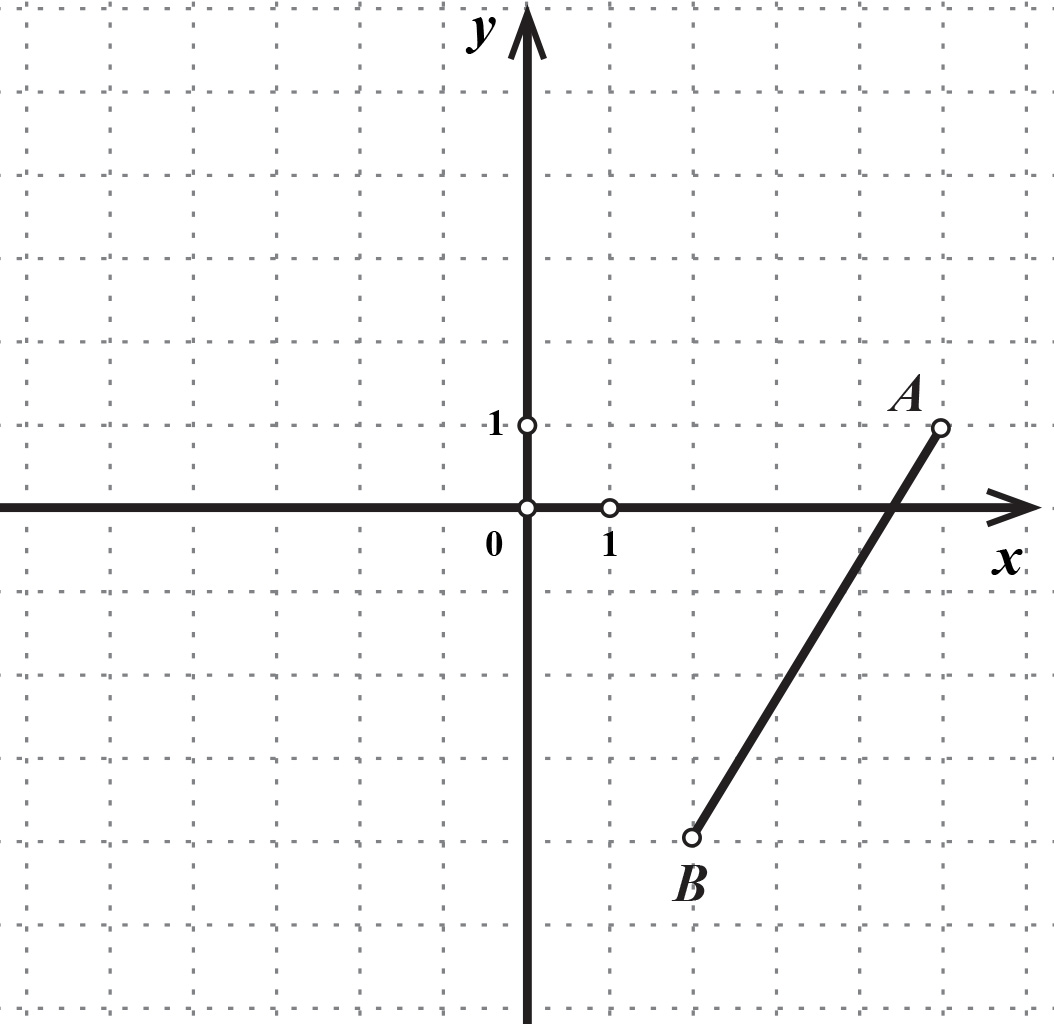
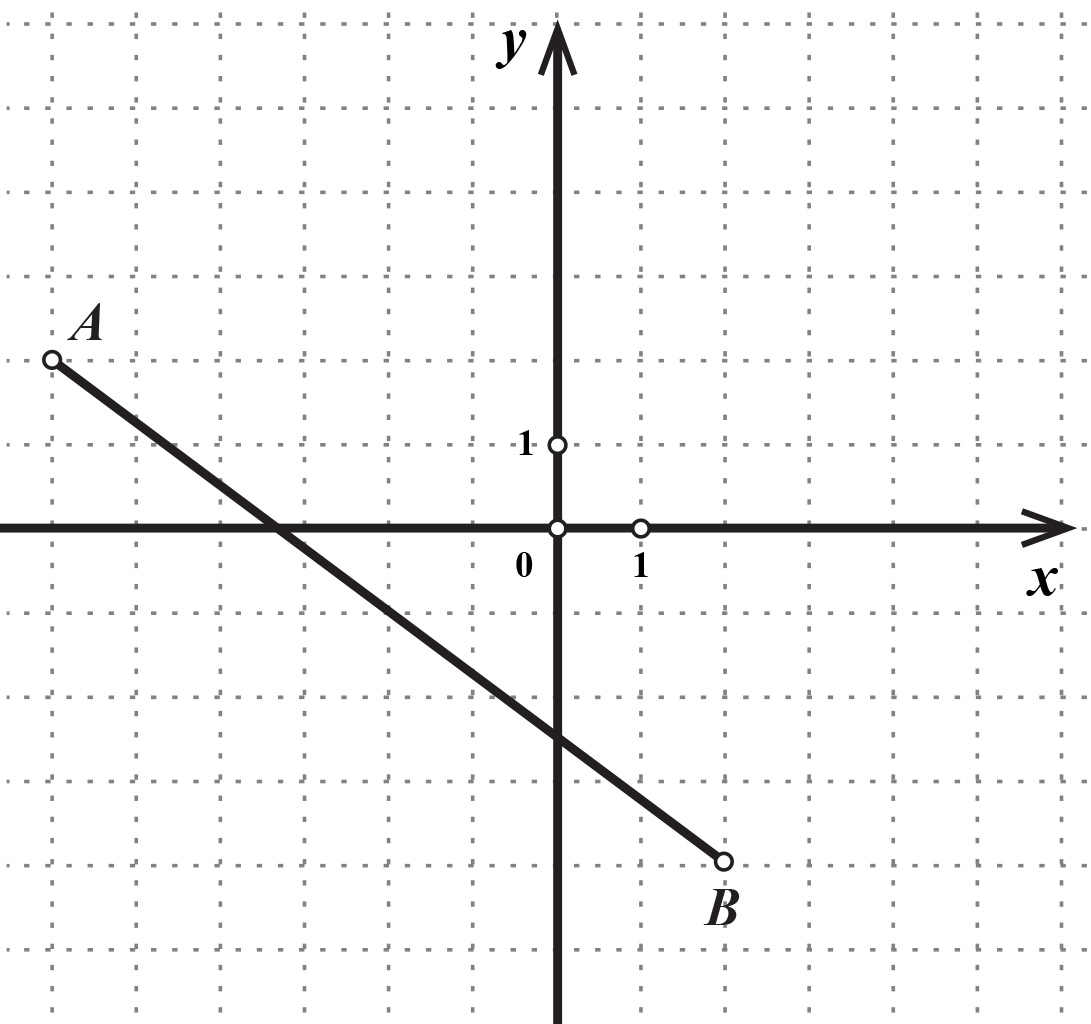
Izračunajte koordinate polovišta dužine primjenjujući formulu.

Polovište je dužine $\bar{A B}$ ako je $A (3, 2)$ i $B (11, 4),$ točka $P ($ , $)$

null

null
Polovište je dužine $\bar{S T}$ ako je $S (- 6, 8)$ i $T (4, 3)$ , točka $P ($ , $) .$

null

null
Polovište je dužine $\bar{R Q}$ ako je $R (- 5, - 3)$ i $Q (2, - 8)$ točka $P ($ , $)$ .

null

null
Polovište je dužine $\bar{M N}$ ako je $M (3.5, 0)$ i $N (0, - 6.5)$ točka $P ($ , $)$ .

null

null

Zatvori

Do sada smo za zadane krajnje točke dužine tražili polovište. Pogledajmo sljedeći primjer.

Primjer 1.

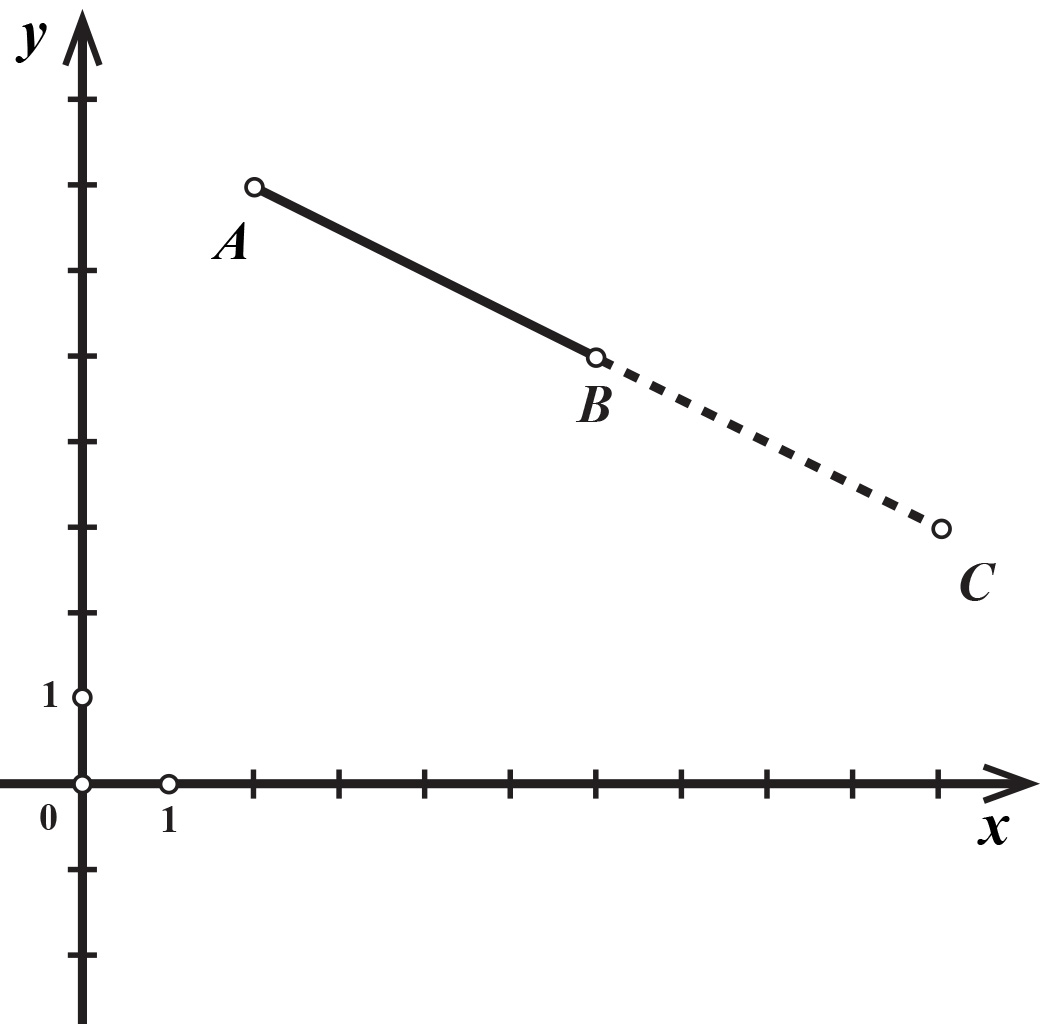
Za zadane točke $A$ i $B$ odredimo točku koja je simetrična točki $A$ s obzirom na točku $B .$ Kako to izgleda?

Točka $C$ simetrična je točki $A$ s obzirom na točku $B .$ Sve tri točke nalaze se na istome pravcu i $|A B| = |B C| .$ To znači da je točka $B$ polovište dužine $\bar{A C} .$

Kako računamo koordinate druge krajnje točke dužine iz zadane jedne krajnje točke i polovišta?

Primjer 2.

Odredimo drugu krajnju točku dužine ako su joj zadani jedna točka $A (3, 7)$ i polovište $P (- 3, 2) .$

Zadatak 4.

Riješite zadatke.

Točka $P (3, 7)$ polovište je dužine $\bar{A B}$ ako je $A (1, - 3)$ i $B ($ , $)$

null

null
Točka $S (0, - 8)$ polovište je dužine $\bar{P T}$ ako je $P (11, - 1)$ i $T ($ , $)$ .

null

null
Točka $K (5, 0)$ polovište je dužine $\bar{M N}$ ako je $M (0.5, 7.2)$ i $N ($ , $)$ .

null

null
Točka $T (- \frac{1}{3}, \frac{1}{5})$ polovište je dužine $\bar{P Q}$ ako je $P (- \frac{17}{3}, \frac{17}{5})$ i $Q ($ , $) .$

null

null

Kutak za znatiželjne

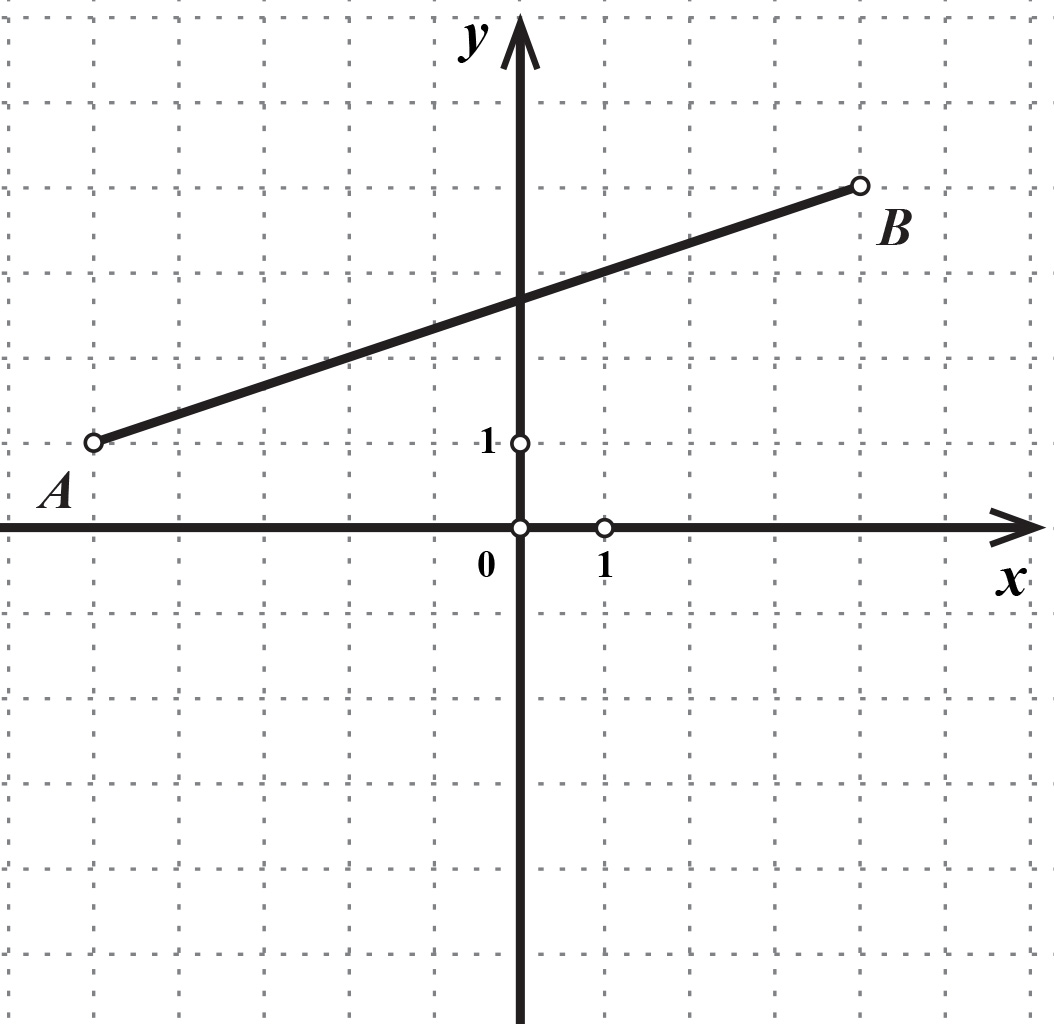
Na slici je koordinatni sustav i dužina koju dijelimo u omjeru 1:2

Polovište dužine dijeli dužinu u omjeru $1 : 1 .$

Dužinu $\bar{A B}$ prikazanu u koordinatnom sustavu podijelite u omjeru $1 : 2 .$

Koje su koordinate točke koja dužinu dijelu u tome omjeru? Možete li napisati formulu za računanje koordinata te točke?

Što ako bismo dijelili dužinu u omjeru $p : q ?$

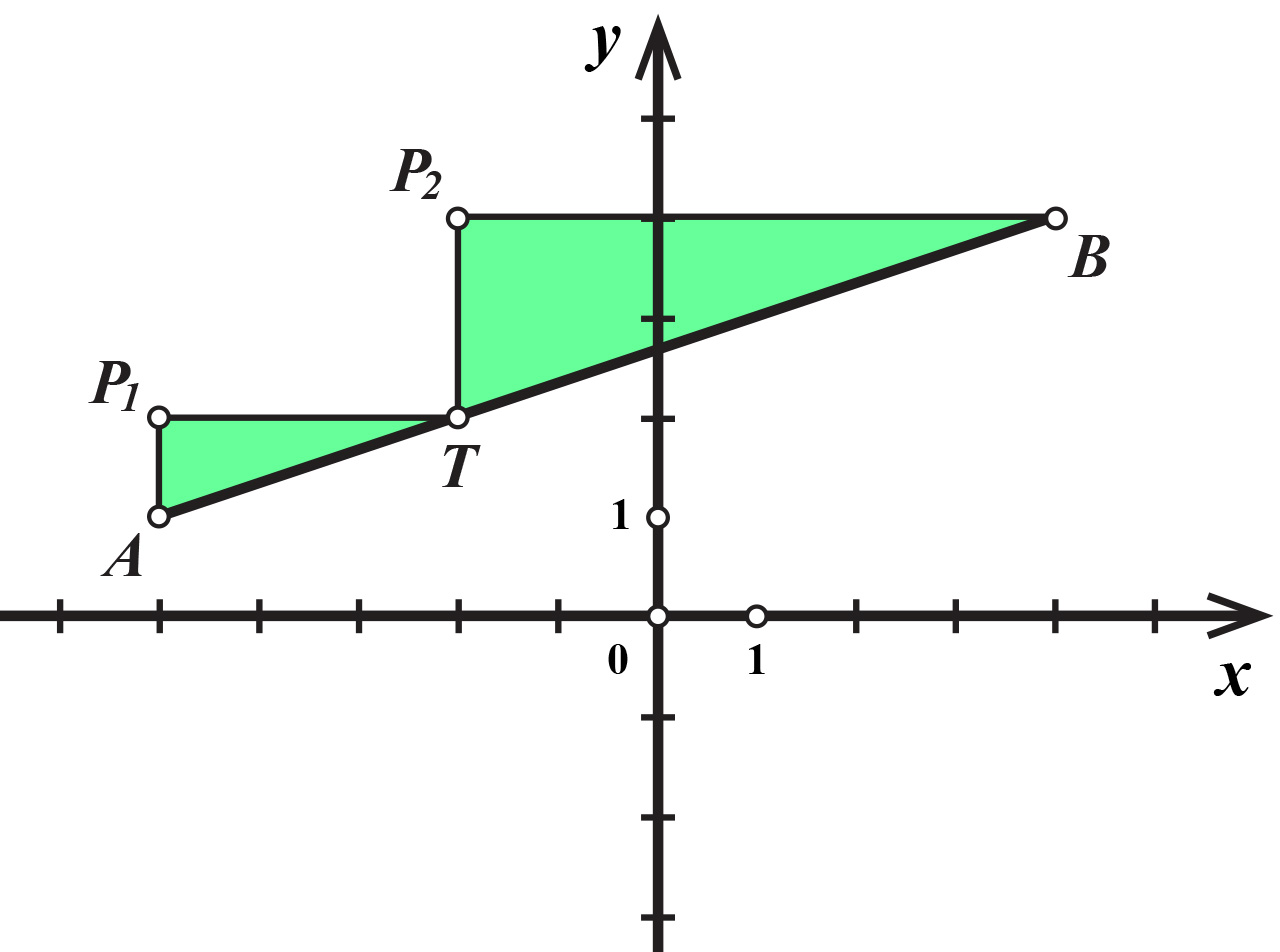
Za dijeljenje dužine u omjeru $1 : 2 :$

Neka su $A (x_{1}, y_{1}),$ $B (x_{2}, y_{2})$ i točka $T (x_{T}, y_{T})$ takva da je $2 \cdot |A T| = |T B| .$

Lako se dokaže da su trokuti $A T P_{1}$ i $T B P_{2}$ slični s koeficijentom sličnosti $2 .$

Tada vrijedi: $\begin{array}{l} 2 (x_{T} - x_{1}) = x_{2} - x_{T} \Rightarrow 3 x_{T} = 2 x_{1} + x_{2} \Rightarrow x_{T} = \frac{2 x_{1} + x_{2}}{3} . \end{array}$

Analogno dobivamo $y_{T} = \frac{2 y_{1} + y_{2}}{3} .$

Slično, za točku $P (x_{P}, y_{P})$ za koju je $q \cdot |A P| = p \cdot |P B|$ vrijedi:

$x_{P} = \frac{q \cdot x_{1} + p \cdot x_{2}}{p + q}$ ; $y_{P} = \frac{q \cdot y_{1} + p \cdot y_{2}}{p + q} .$

5.3 Polovište dužine - dodatni sadržaj

Na početku...