Na početku...

Na kraju godine Ana je sa svojim razredom otputovala na izlet u Rim. Posjetili su mnoge znamenitosti iz vremena staroga Rima, Koloseum, Forum, Fontanu di Trevi i još mnoge druge. Kada su došli na Trg svetog Petra u Vatikanu, vidjeli su ploču na kojoj je pisalo: XIII V MCMLXXXI. Vodič im je rekao da je rimskim brojevima zapisan datum atentata na papu Ivana Pavla II. Ana je taj datum odmah pretvorila u nama razumljiviji oblik. Zatim je pomogla i ostalim članovima grupe da ga pročitaju. Koji je to oblik i koji je to datum?

Ploča na trgu u Vatikanu koja je ugrađena na mjestu gdje je izvršen atentat na Papu, prikazuje datum rimskim brojevima. — Rimski brojevi

Mi se svakodnevno služimo arapskim brojevima pa je Ana, poznavajući pravila rimskog zapisa, prevela datum atentata na arapski zapis, a to je 13. 5. 1981. Usporedimo ta dva zapisa:

ARAPSKI	$1$	$9$	$8$	$1$
	tisućice	stotice	desetice	jedinice
RIMSKI	M	CM	L XXX	I
	tisuću	devetsto $(- 100 + 1 000)$	osamdeset $(50 + 10 + 10 + 10)$	jedan

Oba zapisa napisana su u dekadskom brojevnom sustavu (deka = grčki deset).

A što je to brojevni sustav?

Brojevni sustav

Brojevni sustav jest način zapisivanja brojeva i njihova tumačenja.

Sastoji se od:

skupa znamenaka
pravila za pisanje znamenaka.

Zanimljivost

Tablica rimskih i arapskih brojeva:

RIMSKI	ARAPSKI
I	$1$
V	$5$
X	$10$
L	$50$
C	$100$
D	$500$
M	$1000$

Pravila za pisanje/čitanje rimskih brojeva i pretvarač u arapski sustav možeš koristiti na ovoj stranici.

Koja je osnovna razlika između arapskog i rimskog zapisa brojeva?

U arapskom zapisu svakoj znamenci raste vrijednost s desne strane prema lijevoj.

Što je s rimskim brojevima? Promotri broj XXX. Koja je vrijednost pojedinog X-a?

Raste li vrijednost znamenke zdesna nalijevo?

Ne, svaka znamenka X ima jednaku vrijednost bez obzira na kojem mjestu se nalazi.

XXX $= 10 + 10 + 10 = 30$

Iz ovoga možemo zaključiti sljedeće.

Postoje $2$ vrste brojevnih sustava:

POLOŽAJNI	NEPOLOŽAJNI
sastoje se od znamenaka čija vrijednost raste zdesna nalijevo (jedinice, desetice, stotice, tisućice…) vrijednost znamenke ovisi o njezinu položaju u broju. Na primjeru godine 1981., znamenka $1$ ima različitu vrijednost ako je na položaju skroz desno (vrijednost $1$ ) i ako je na položaju skroz lijevo (vrijednost $1000$ )	vrijednost znamenke čita se redom kako je napisana prema posebnim pravilima

Nakon što upoznaš pravila za pisanje/čitanje rimskih brojeva koja se nalaze u dijelu Zanimljivosti, spoji iste vrijednosti brojeva zapisane na dva načina: rimskim i arapskim brojevnim sustavom!

LXX
XLV
CCII
MDX

Pomoć:

U dijelu Zanimljivosti nalazi se poveznica s pravilima pisanja/čitanja rimskih brojeva.

DEKADSKI BROJEVNI SUSTAV

Deset prstiju iznad kojih su brojke od 1 do 10. — Deset prstiju

U svakodnevnoj uporabi koristimo dekadski brojevni sustav. Zašto?

Vjerojatno zbog toga što imamo deset prstiju.

Od koliko se različitih znamenaka sastoji taj sustav?

Sastoji se od $10$ znamenaka, a to su $0 1 2 3 4 5 6 7 8 9 .$

Baza brojevnog sustava

Broj znamenaka u nekom sustavu naziva se baza brojevnog sustava. Najmanja je znamenka svakog sustava $0,$ dok je najveća znamenka za jedan manja od baze.

Na primjer, ako je baza $6,$ njezine su znamenke $0 1 2 3 4 5 .$

Kolika bi onda bila baza dekadskog sustava?

Baza dekadskog sustava jest $10,$ a zapisuje se indeksom s desne strane broja.

Pomoću tih deset znamenaka možemo stvoriti bezbroj brojeva.

Vrijednost znamenke u broju raste zdesna nalijevo, odnosno ovisi o položaju u broju. Možemo reći da položaj u broju određuje težinsku vrijednost znamenke ili njezinu težinu.

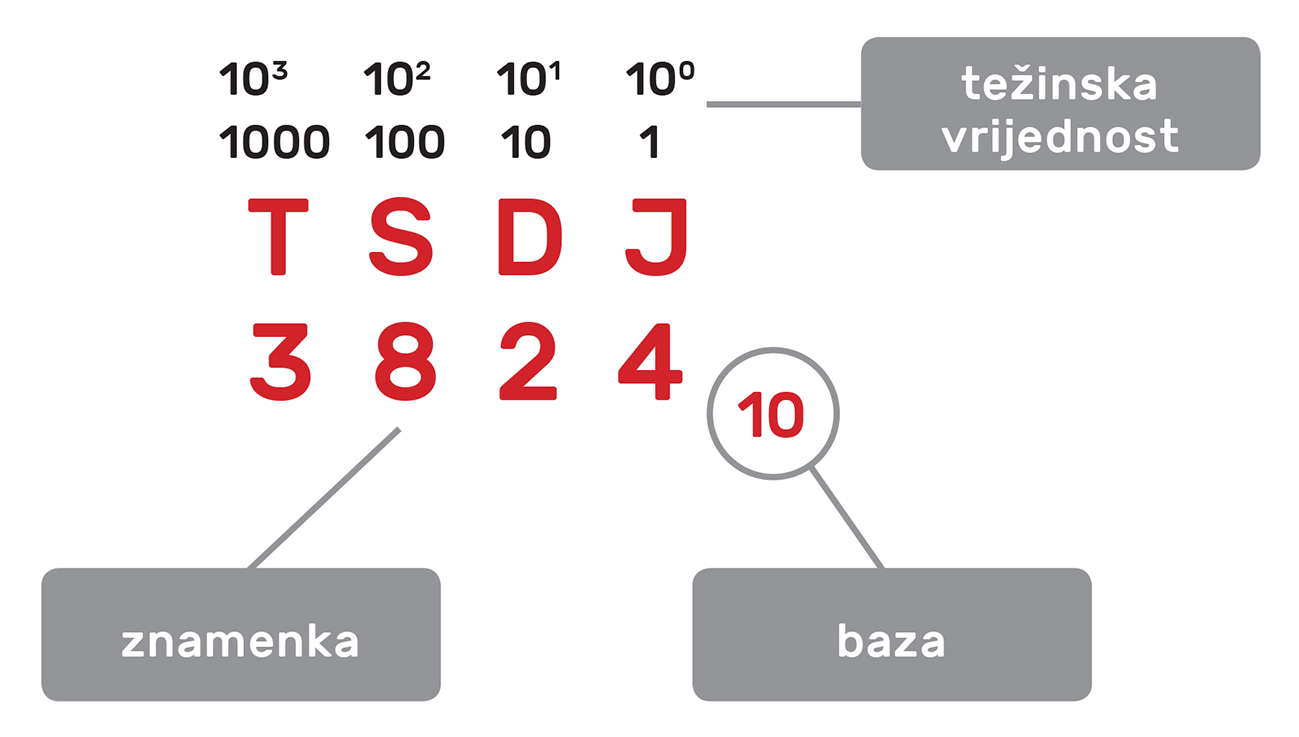
Zapis dekadskog broja s bazom i težinskim vrijednostima. — Dekadski sustav

TEŽINSKA VRIJEDNOST ZNAMENKE

Promotrimo broj $3824_{10}$ sa slike. Kolika je vrijednost pojedinih znamenaka toga broja? Već smo spomenuli jedinice, desetice, stotice, tisućice... Zašto ih tako zovemo?

U našem slučaju znamenka $3$ označava tisućicu. Kojim brojem treba pomnožiti znamenku 3 da dobijemo njezinu vrijednost? Treba je pomnožiti s $1000$ $(10^{3})$ ; da dobijemo stotice, znamenku $8$ množimo brojem $100$ $(10^{2}),$ znamenku $2$ množimo brojem $10$ $(10^{1})$ da dobijemo desetice, a znamenku $4$ množimo brojem $1$ $(10^{0})$ da dobijemo jedinice. Vrijednost broja jest zbroj dobivenih vrijednosti svih znamenaka.

Preglednije, možemo napraviti takozvanu tablicu težinskih vrijednosti:

.....	$10^{3}$	$10^{2}$	$10^{1}$	$10^{0}$
	$3$	$8$	$2$	$4$

Vrijednost broja napisanoga u drugom redu tablice jest:

$3 * 10^{3} + 8 * 10^{2} + 2 * 10^{1} + 4 * 10^{0} = 3000 + 800 + 20 + 4 = 3824_{10}$

Zaključak: Da bismo dobili vrijednost broja u dekadskome sustavu, svaka znamenka množi se počevši zdesna s potencijama baze ( $10$ ) i to najprije nultom potencijom, $10^{0},$ a zatim s $10^{1},$ $10^{2},$ $10^{3} ...$

Na kraju zbrojimo dobivene vrijednosti.

Broj $2547_{10}$ razvrstaj prema pripadnim težinskim vrijednostima njegovih znamenaka:

5

4

2

7

Desetice

Tisućice

Stotice

Jedinice

Pomoć:

Vrijednost znamenki broja u položajnom brojevnom sustavu ovisi o njihovom položaju. Krajnje desno su jedinice (znamenka se množi brojem 1), zatim slijede desetice ( znamenka se množi brojem 10), stotice (množi se brojem 100) i tisućice (množi se brojem 1000)

Postupak:

$2547_{10} = 2 * 1000 + 5 * 100 + 4 * 10 + 7 * 1$

U dekadskome sustavu brojeve od $0$ do $9$ zapisujemo jednom znamenkom. Kako zapisujemo broj za jedan veći od $9 ?$ Potrebne su nam dvije znamenke. Koliko brojeva možemo zapisati s dvije znamenke? Od $10$ do $99 .$ Kako dalje, kako zapisati broj za $1$ veći od $99 ?$ Potrebne su nam $3$ znamenke da zapišemo $100,$ itd.

Mi smo navikli na dekadski brojevni sustav, ali postoje sustavi koji imaju manju ili veću bazu od $10 .$

Pažljivo pogledaj video u kojem su opisani različiti brojevni sustavi i način na koji tvore brojeve.

Ako brojevni sustav koristi znamenke

0 1 2 3 4 5 6,

kolika je njegova baza?

Baza brojevnog sustva predstavlja broj znamenki u tom sustavu.

Pomoć:

Baza brojevnog sustva predstavlja broj znamenki u tom sustavu. Ovaj sustav ima $7$ različitih znamenki pa kažemo da ima bazu $7 .$

Postupak:

Ovaj sustav ima $7$ različitih znamenki pa kažemo da ima bazu $7 .$

Brojevni sustavi s bazom manjom od 10

Pokušajmo napraviti tablice težinskih vrijednosti za nekoliko brojevnih sustava.

BAZA 5

.....	$5^{2}$	$5^{1}$	$5^{0}$
	$1$	$2$	$3$

Vrijednost broja napisanoga u drugom redu tablice jest:

$123_{5} = 1 * 5^{2} + 2 * 5^{1} + 3 * 5^{0} = 1 * 25 + 2 * 5 + 3 * 1 = 38_{10}$

Zadatak 1.

BAZA 7

Broj $1136,$ zapisan u drugom redu tablice s težinskim vrijednostima baze $7,$ napiši u dekadskom obliku:

$7^{3}$	$7^{2}$	$7^{1}$	$7^{0}$
$1$	$1$	$3$	$6$

Pogledaj pomoć!

Pomoć:

Znamenke broja u 2. redu tablice pomnoži s potencijama baze iznad njih.

Postupak:

$1136_{7} = 1 * 7^{3} + 1 * 7^{2} + 3 * 7^{1} + 6 * 7^{0} = 343 + 49 + 21 + 6 = 419_{10}$

BAZA 2

Od kojih se znamenaka sastoji broj s bazom $2 ?$

Od znamenaka $0$ i $1 .$ Jesu li ti poznate ove vrijednosti iz prethodnih jedinica? U računalu se svi podaci prikazuju pomoću nula i jedinica, zbog toga nam je ovaj sustav posebno zanimljiv.

Za ovaj sustav proširit ćemo tablicu težinskih vrijednosti da možemo upisati veće brojeve.

$2^{7}$	$2^{6}$	$2^{5}$	$2^{4}$	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$
		$1$	$0$	$1$	$1$	$0$	$0$

Broj 101100, zapisan u drugom redu gornje tablice s težinskim vrijednostima baze

2,

napiši u dekadskom obliku:

Pogledaj pomoć!

Pomoć:

Sve znamenke $1$ pomnožimo s težinskim vrijednostima iznad njih i zatim zbrojimo rezultate.

Postupak:

$101100_{2} = 32 + 8 + 4 = 44_{10}$

Brojevni sustavi s bazom većom od 10

Koristimo li sustav s bazom većom od $10,$ znamenke nakon $9$ zapisujemo pomoću velikih slova engleske abecede: A B C D E F G H...

BAZA 12

$12^{4}$	$12^{3}$	$12^{2}$	$12^{1}$	$12^{0}$
		$1$	A	B

Prisjetimo se da je vrijednost znamenke A = $10,$ a znamenke B = $11 .$

Dekadska vrijednost broja napisanoga u drugom redu tablice jest:

$1 * 12^{2} + A * 12^{1} + B * 12^{0} = 1 * 144 + 10 * 12 + 11 * 1 = 144 + 120 + 11 = 275_{10}$

Zadatak 2.

BAZA 16

Broj BC iz sustava s bazom

16

zapiši u dekadskom sustavu.

Težinska vrijednost znamenaka u sustavu s bazom

16

jest

16 .

Znamenka B ima vrijednost

11,

a znamenka C vrijednost

12 .

Pomoć:

U sustavu s bazom $16$ težinska vrijednost znamenaka jest $16 .$ Znamenka B ima vrijednost $11,$ a znamenka C vrijednost $12 .$

Postupak:

$B C_{16} = B * 16^{1} + C * 16^{0} = 11 * 16 + 12 * 1 = 176 + 12 = 188_{10}$

Pretvaranje broja iz dekadskog u bilo koji brojevni sustav

Do sada smo brojeve iz raznih sustava prikazivali u dekadskome sustavu. Kako napraviti obrnuti postupak, zapisati dekadski broj u nekom drugom sustavu?

Broj se uzastopce dijeli s bazom sustava, a pritom se zapisuju cjelobrojni ostaci. Kada dobijemo rezultat dijeljenja 0, svi ostaci zapisuju se obrnutim redoslijedom.

Na primjer:

$83_{10} = ?_{6}$

	ostatak
$83 : 6 = 13$	$5$
$13 : 6 = 2$	$1$
$2 : 6 = 0$	$2$	$↑$

$83_{10} = 215_{6}$

Zadatak 3.

Dekadski broj $125$ prikaži u $4$ različita brojevna sustava:

BAZA 2:

BAZA

16:

Pomoć:

Broj uzastopce dijelimo bazom a pri tome zapisujemo cjelobrojne ostatke. Kada kao rezultat dobijemo $0,$ ostatke zapišemou obrnutim redoslijedom.

Postupak:

BAZA 2

	ostatak
$125 : 2 = 62$	$1$
$62 : 2 = 31$	$0$
$31 : 2 = 15$	$1$
$15 : 2 = 7$	$1$
$7 : 2 = 3$	$1$
$3 : 2 = 1$	$1$
$1 : 2 = 0$	$1$	$↑$

$125_{10} = 1111101_{2}$

BAZA 4:

	ostatak
$125 : 4 = 31$	$1$
$31 : 4 = 7$	$3$
$7 : 4 = 1$	$1$
$1 : 3 = 0$	$1$	$↑$

$125_{10} = 1331_{4}$

BAZA 8:

	ostatak
$125 : 8 = 15$	$5$
$15 : 8 = 1$	$7$
$1 : 8 = 0$	$1$	$↑$

$125_{10} = 175_{8}$

BAZA 16:

	ostatak
$125 : 16 = 7$	$13$	$> D$
$7 : 16 = 0$	$7$	$↑$

$125_{10} = {7D}_{16}$

Što možemo zaključiti nakon analize rješenja iz prethodnog zadatka? Gdje smo računali najdulje, a gdje najkraće? Postoji li neka veza između baze i duljine zapisa broja?

Isprobaj ovaj brojevni pretvarač. Pritom razmišljaj i o duljini zapisa u pojedinom brojevnom sustavu.

Povećaj interaktivni prikaz

Kutak za znatiželjne

Prema svemu što je rečeno o brojevnim sustavima pokušaj riješiti ove zadatke:

Ako u dekadskom sustavu brojeve od

0

9

zapisujemo jednom znamenkom, brojeve veće od

9

pomoću

2

znamenke (

10,

11,

12, .

...), razmisli: Kako bismo zapisali brojeve s bazom

5 ?

Taj sustav ima znamenke

0 1 2 3 4 .

Kako bismo prikazali broj za

1

veći od

4 ?

Težinska vrijednost u brojevnom sustavu s bazom

5

iznosi

5 .

Dakle, svaka znamenka množi se brojem

5

počevši zdesna. Jednostavnije, krajnju desnu znamenku množimo s

1

ili nultom potencijom baze, a svaku sljedeću s većom potencijom baze

2,

3 ...

Koji

je broj sljedeći, za

2

veći od broja

4 ?

Pogledaj pomoć!

Pomoć:

Težinska vrijednost u brojevnom sustavu s bazom $5$ iznosi $5$ . Dakle, svaka znamenka množi se brojem $5$ počevši zdesna. Jednostavnije, krajnju desnu znamenku množimo s $1$ ili nultom potencijom baze, a svaku sljedeću s većom potencijom baze $2$ , $3$ ...

Postupak:

$10_{5} = 1 * 5^{1} + 0 * 5^{0} = 5 + 0 = 5_{10}$

$11_{5} = 1 * 5^{1} + 1 * 5^{0} = 5 + 1 = 6_{10}$

Dekadskim vrijednostima na lijevoj strani pridruži odgovarajuću vrijednost zapisanu u sustavu s bazom $4 .$

$1$
$2$
$3$
$4$
$5$
$6$
$7$
$8$
$9$
$10$
$11$
$12$
$13$
$14$
$15$
$16$
$17$
$18$
$19$
$20$

Pomoć:

U sustavu s bazom $4,$ znamenke su $0,$ $1,$ $2,$ i $3 .$ Nakon broja $3$ sljedeća znamenka zapisuje se pomoću $2$ znamenke, odnosno kao $10 .$

null

...i na kraju

Iz navedenih primjera vidljivo je da se svaki broj može zapisati na različite načine, u različitim brojevnim sustavima. Sustavi s bazom $2$ (binarni), $8$ (oktalni) i $16$ (heksadekadski) koriste se u informatici. O njima će više riječi biti u sljedećim poglavljima.

Procijenite svoje znanje

Kako se naziva brojevni sustav u kojem vrijednost znamenke ovisi o njenom položaju u broju?

dekadski

oktalni

položajni

rimski

null

Baza brojevnog sustava zapisuje se:

desno od broja kao indeks

iznad broja kao potencija

lijevo od broja

null

Najmanja težinska vrijednost u svim položajnim sustavima jest $1 .$

null

Uparite brojeve u različitim sustavima s njihovim dekadskim zapisom

$100_{8}$	$165_{10}$
$10001100_{2}$	$50_{10}$
$302_{4}$	$64_{10}$
$A 5_{16}$	$140_{10}$

Pomoć:

Broj iz neke baze pretvori u dekadski zapis i pronađi odgovarajuću dekadsku vrijednost.

null

Ako bismo radili s brojevnim sustavom baze

20,

koju bi vrijednost imala znamenka J?

Pomoć:

U sustavima s bazom većom od $10,$ znamenke nakon broja $9$ zapisuju se slovima engleske abecede: A, B, C, D .... ( $10$ = A, $11$ = B, $12$ = C, $13$ = D, ..... ?=J)

null

4.1 Brojevni sustavi

Na početku...

Brojevni sustav

Zanimljivost

DEKADSKI BROJEVNI SUSTAV

Baza brojevnog sustava

Desetice

Tisućice

Stotice

Jedinice

Brojevni sustavi s bazom manjom od 10

Zadatak 1.

Brojevni sustavi s bazom većom od 10

Zadatak 2.

Pretvaranje broja iz dekadskog u bilo koji brojevni sustav

Zadatak 3.

Kutak za znatiželjne

...i na kraju

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: