Kad je Marta počela objašnjavati, vidjela je da to i nije tako jednostavno objasniti nekome tko ne zna mnogo o računalima. Pa je krenula od početka. Prisjetila je svoju prijateljicu da je iz informatike učila o memoriji računala.

Memorija računala sastoji se od malih elektroničkih sklopova (bistabila) koji mogu biti u dva stanja: $0$ (niži napon) i $1$ (viši napon).

Jedna binarna znamenka ili bit može primiti vrijednost $0$ ili $1.$ Logično je da jedan bistabil uvijek pamti jednu binarnu znamenku bit.

Ako želimo pohraniti više bitova, trebat će nam više povezanih bistabila. Takav skup bistabila naziva se registar. Je li za sada jasno?   

• $1$ bistabil pohranjuje $1$ bit        
  
• $1$ registar pohranjuje više bistabila (bitova).

Ovisno o podatku koji treba pohraniti, veličina registra može biti različita. Tako postoje registri od $8$ bitova, $16$ bitova, $32$ i $64$ bita. Prepoznaješ li ove brojeve? To su potencije broja $2,$ a zašto? Jer se radi o binarnom brojevnom sustavu!

• duljina od $8$ bitova naziva se bajt

To ti je sigurno poznato. Bajt je najmanja mjerna jedinica za kapacitet memorije. A sigurno si čula i za kibibajt, mebibajt, gibibajt i tako dalje. To su veće jedinice za kapacitet memorije.

Također, važno je želimo li zapisati prirodni, negativni ili decimalni broj. Postoje različite metode i pri zapisu je uvijek važno naglasiti o kojoj se metodi radi.

Na primjer, broj $5$ za koji si me pitala može biti zapisan na različite načine. Za početak pretvorimo broj $5$ u binarni sustav: $5_{10}={101}_2.$ Dakle, mogao bi se prikazati najmanje u $4$ bita kao 0101.

Binarni broj zapisujemo zdesna prema lijevo. Budući da dobiveni broj pohranjujemo u registar od $8$ bitova, u preostala prazna mjesta unose se nule pa to izgleda ovako:

a radi li se o 16-bitnom registru, izgleda ovako:

Sofija: A zašto koristimo $16$ bitova kada tu ima toliko nepotrebnih nula?

Marta: Zato što možda računalo u svome radu koristi 16-bitne registre. Mi ćemo radi jednostavnosti koristiti 8-bitne registre za manje brojeve, a veće registre za veće brojeve.

Na primjer, provjerimo u kakav će registar računalo smjestiti broj $280.$

${280}_{10}={100011000}_2.$

Ovaj broj može se smjestiti u najmanje $12$ znamenaka: 000100011000. Zbog toga ga se ne može pohraniti u registar od $8$ bitova, već ga je potrebno pohraniti u registar od $16$ bitova. U preostala prazna mjesta unesu se nule, pa to izgleda ovako:

A želimo li zapisivati i negativne brojeve, onda nam treba ova metoda:

Skup cijelih brojeva čine pozitivni i negativni brojevi. Ispred negativnog broja zapisujemo znak $-$ (minus), a znak $+$ ispred pozitivnog broja obično ne pišemo.

Sofija: Ali kako ćemo napisati + ili - ako u bistabilu mogu biti samo $2$ stanja: $0$ ili $1?$
Marta: Dobro pitanje, tu se radi o dogovoru, prvi bit iskoristit ćemo za predznak:

• ako je broj pozitivan, u prvi bit zapisujemo $0$
• ako je broj negativan, u prvi bit zapisujemo $1.$

Na primjer, zapišimo broj $-9.$ Prikažimo broj $9$ u binarnom obliku: $9_{10}={1001}_2.$

Dobiveni binarni broj upisujemo zdesna, popunjavamo vodećim nulama, a prvi bit koji predstavlja predznak postavljamo na $1.$

    $\downarrow$                              $\downarrow$        

predznak         apsolutna vrijednost

Zapravo, uvijek prikažemo apsolutnu vrijednost broja, a zatim odredimo predznak, zato se ova metoda tako i zove.

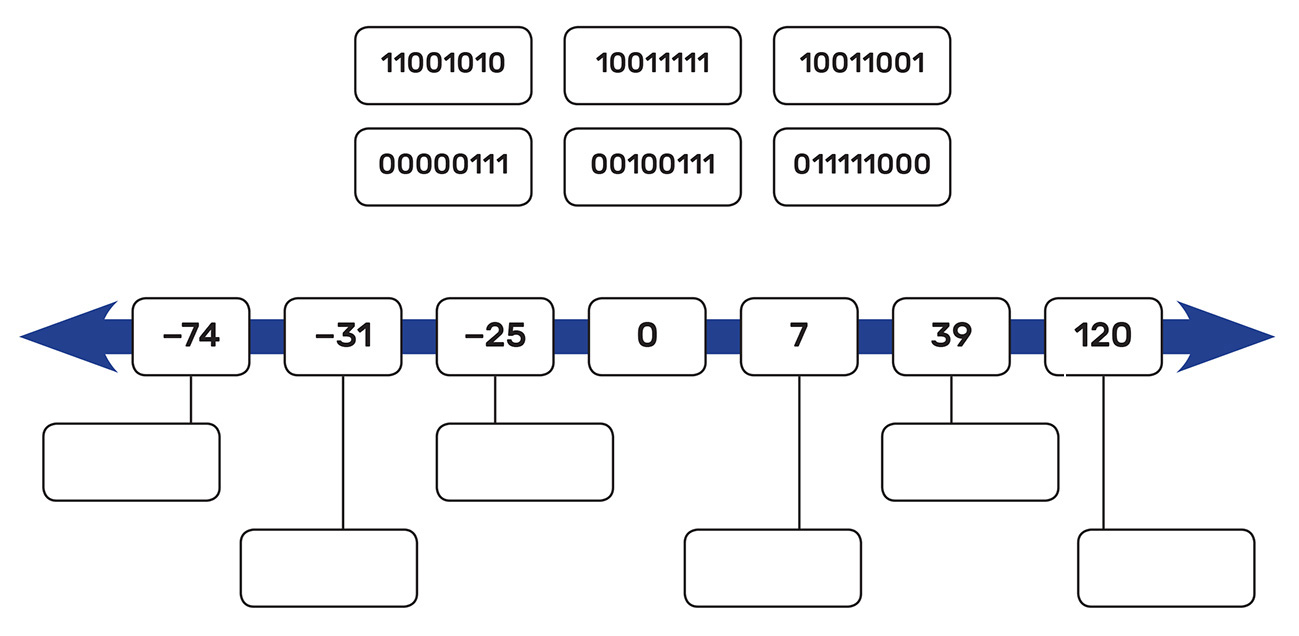
Sofija: Ali sada imamo jedan bit manje za zapis brojeva, kada ga koristimo za predznak.

Marta: Tako je, ali predznak moramo na neki način zapisati. Veći su problem računske operacije u takvom sustavu. Treba voditi računa zbrajaju li se brojevi istog  ili različitog predznaka. Zato se negativni brojevi češće zapisuju metodom dvojnog komplementa koju smo naučili u jedinici Zbrajanje brojeva u binarnom brojevnom sustavu.

Pa da vidimo u čemu je razlika!

Sofija : Ako je broj zapisan metodom dvojnog komplementa, hoćemo li napraviti obrnuti postupak, oduzeti jedinicu, zamijeniti nule i jedinice... da bismo dobili dekadski oblik broja?

Marta: Ma ne, to se izračuna vrlo jednostavno. Znamenke binarnog broja množiš s odgovarajućim težinskim vrijednostima, samo paziš da krajnji lijevi bit ima negativan predznak. Na primjer, radi li se o 8-bitnom registru, vodeći bit množimo s $-128$ ( $2^7$).

Evo na primjeru:

Koji je dekadski broj zapisan u 8-bitnom registru ako se radi o metodi dvojnog komplementa?

Rješenje:

$\begin{array}{l}-1*2^7+1*2^6+1*2^5+1*2^4+1*2^3+1*2^2+0*2^1+1*2^0=-128+64+32+16+8+4+0+1=-128+125=-3\end{array}$

A sad pokušaj samostalno:

Sofija: Sad baš razmišljam, zapravo je za pozitivni broj svejedno kojom se metodom zapisuje.

Marta: Točno, samo će negativni broj biti različito zapisan ovisno o tome kojom smo se metodom koristili, metodom predznaka i apsolutne vrijednosti ili dvojnog komplementa.

Sofija: A kako se zapisuju decimalni brojevi? Kako ćemo znati gdje je decimalna znamenka? Imamo li i za nju poseban bit?

Marta : Realni se brojevi mogu zapisati na dva načina:

• s pomičnom točkom (eksponencijani prikaz)
  
• s fiksnom točkom.

Prikaz s fiksnom točkom nije praktičan jer koristi fiksni dio registra za prikaz cijelog broja i fiksni dio za prikaz decimalnog dijela broja. Na taj je način prostor u registru loše iskorišten. Na primjer, brojevi $3.1024$ i $325.4$ koristili bi jednake fiksne dijelove za cijeli i decimalni dio.

Sofija: Što to znači eksponencijalni prikaz? Zvuči mi poznato.

Marta: Poznato ti je jer se tako prikazuju jako veliki ili jako mali brojevi. Još se zove i znanstveni zapis.

Na primjer, možeš li pročitati broj stanovnika na Zemlji: $7530000000.$ Bilo bi lakše da ga zapišeš kao $7.53*{10}^9.$ Ili kad smo učili da je masa elektrona jednaka oko $0.0000000000000000000000000000009109kg.$ Teško je pročitati takav broj pa se zapisuje kao $9.109*{10}^{-31}.$

Kako nastaje znanstveni prikaz broja objašnjeno je u videu koji slijedi:

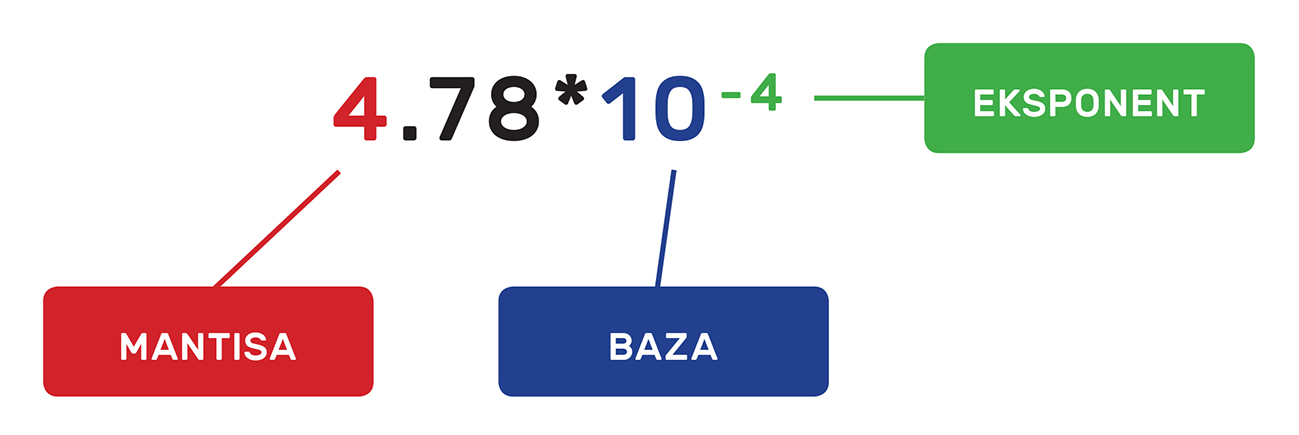
Evo nekoliko zadataka za vježbu. 

A sad nam još ostaje zapisati realni broj u računalo. Neka to bude broj $34.75.$

Najprije broj treba pretvoriti u binarni zapis.

Nadam se da se sjećaš, upute pogledaj u jedinici Binarni brojevni sustav.

I da napokon smjestimo broj $34.75$ u računalni registar od $32$ bita.

Sofija: A zašto baš $32$ bita?

Marta: Zato što se pomoću standarda IEEE $754$ mogu zapisati brojevi s jednostrukom preciznošću ( $32$ bita) i s dvostrukom preciznošću ( $64$ bita). Mi ćemo koristiti jednostruku preciznost. U registru od  $32$ bita broj se sprema na sljedeći način:

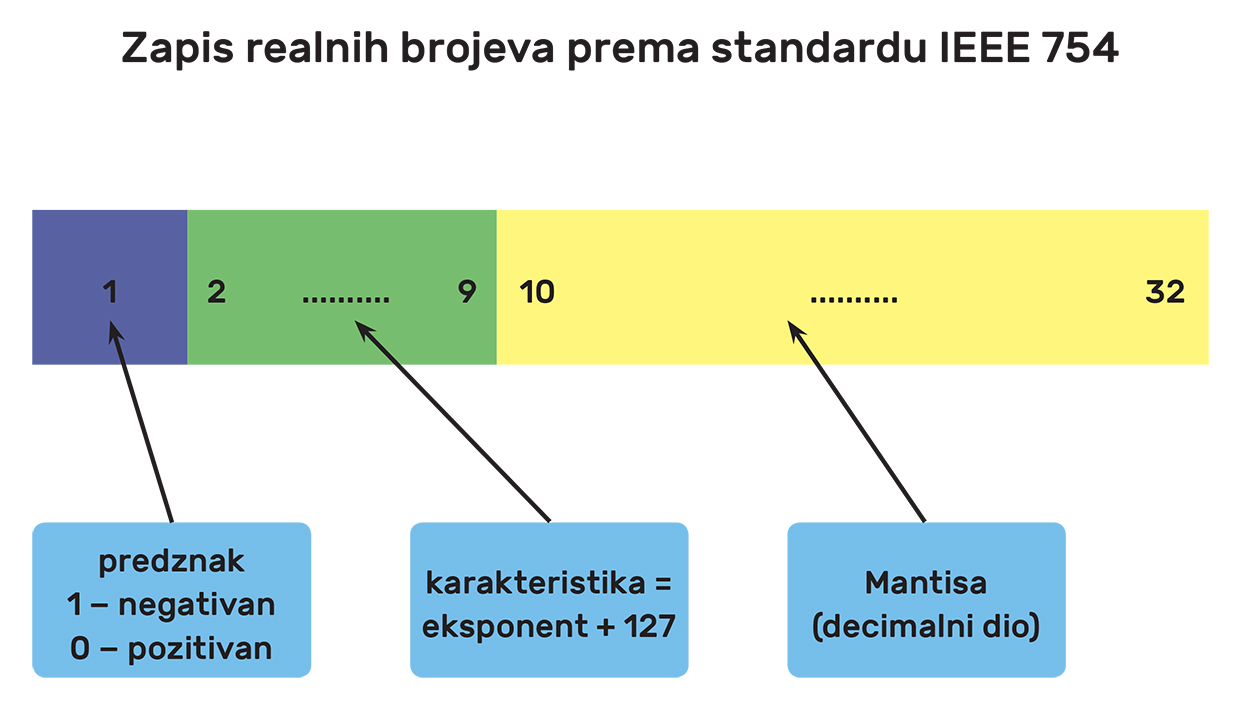
Na primjeru broja ${34.75}_{10}:$

1. PREDZNAK (upisuje se u 1. bit: $0$ za pozitivne, a $1$ za negativne brojeve), dakle $0.$
2. Realan broj pretvorimo u binarni ${34.75}_{10}={100010.11}_{2.}$
3. Dobiveni binarni broj zapišemo u eksponencijalnom obliku $1.0001011*2^5.$

Od dobivenog broja određujemo:

MANTISU (decimalni dio) $0001011$

KARAKTERISTIKU: eksponent + $127$ ( $5+127=132$), u binarnom obliku $10000100.$

I napokon, naš broj izgleda ovako:

p = predznak

Sadrži li mantisa manje od $23$ bita, dopunjavamo je nulama.

Sofija: Imam dva pitanja: Zašto se upisuje samo decimalni dio mantise i zašto se eksponentu dodaje $127?$

Marta: Kod mantise je cijeli dio uvijek $1$ jer smo decimalnu oznaku pomicali do jednog cijelog koji je različit od nule. Zašto zapisivati znamenku za koju znamo da je $1?$ Ovu jedinicu zovemo skriveni bit.

Karakteristiku dobijemo tako da eksponentu dodamo $127$ jer tako osiguravamo da nemamo negativan eksponent. (U 8-bitnom registru najveći negativni broj koji možemo zapisati jest $-127$ pa se dodavanjem broja $127$ osigurava da karakteristika ne može biti negativna.)

Takav je 32-bitni zapis nepregledan pa se koristi heksadekadski zapis broja. Imaš li ideju kako heksadekadski zapisati taj broj?

Grupira se po $4$ znamenke ( $32:4=8$) i heksadekadski zapis sigurno će imati $8$ znamenaka.

Sofija: Uf, ovo je bilo naporno, ali mi je sve jasno. Treba samo samostalno provježbati.

Marta: Evo jedan zadatak za vježbu:

A sada jedan obrnuti zadatak. Koji je broj zapisan u ovom registru?

PREDZNAK: $0$ znači da je broj pozitivan.

KARAKTERISTIKA: ${01111100}_2={124}_{10}$

• Računamo $124-127=-3.$
• EKSPONENT: $=-3.$

MANTISA (decimalni dio) : 01000000000000000000000

MANTISA: dodajemo skriveni bit odnosno cijeli dio mantise $1.01$ (nule možemo odbaciti)