Informatika 1 - Aktivnosti za samostalno učenje

Na početku...

Na slici je binarni sat. Postoje različite vrste binarnih satova. Pronađi na internetu više o njima.

Okrugli binarni sat na ruci. — Binarni sat

Koliko sati pokazuje ovaj binarni sat?

koliko minuta?

Pomoć:

Pogledaj koje su lampice upaljene, a koje ugašene.

Postupak:

Zbrajamo vrijednosti uključenih lampica:

SAT:	MINUTE:
$\begin{array}{l} 8 & 4 & 2 & 1 \\ 0 & 0 & 1 & 1 \end{array}$	$\begin{array}{l} 32 & 16 & 8 & 4 & 2 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 \end{array}$
$3$	$25$

Zadatak 1.

Maja šalje svojoj prijateljici šifriranu poruku 100 (jedan nula nula). To znači da će se naći u

4

sata. Koju poruku treba poslati ako se žele naći u

12

sati?

Pomoć:

Broj $12$ pretvoriti iz dekadskoga u binarni sustav.

Postupak:

Broj $4$ u dekadskome sustavu je 100 u binarnome.

Broj $12$ u dekadskome je 1100 u binarnome.

Zadatak 2.

Pokušaj riješiti nekoliko zadataka s međunarodnog natjecanja Dabar.

Smeđi dabar, maskota istoimenog natjecanja iz informatike i računalnog razmišljanja. Dabar je nasmijan, ima isturene prednje zube, a na plosnatom se repu nalazi motiv crveno-bijele šahovnice. — Dabar

Kako bi se olakšala razmjena dobara u šumi gdje su stanovnici dabrovi, dabrovi su uveli novu valutu koju nazivaju ''beuri''. Kovanice su u vrijednosti

1,

2,

4

8

. No dabrovi su vrlo štedljivi pa zato uvijek žele potrošiti malo novaca. Koliko najmanje kovanica mogu iskoristiti da bi dobili vrijednost od

14

beura?

Pomoć:

Pogledaj nastavnu jedinicu Binarni brojevni sustav.

Stanovnici Dabrove staze naručili su jedanaest pizza. Raznosač pizza ne zna koliko pizza treba dostaviti u svaku kuću. Kraj svake kuće stoji znak koliko pizza ukućani žele. Ispred jedne kuće zaboravili su izbrisati stari natpis. Ispred koje je to kuće?

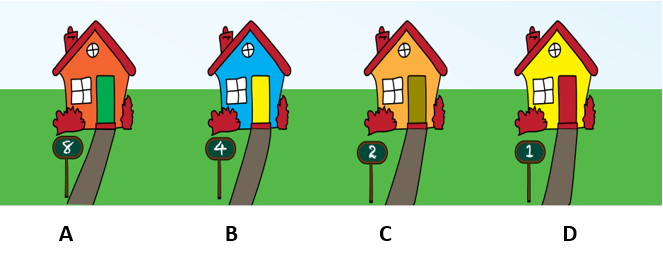
Ilustracija prikazuje četiri kućice na dabrovoj stazi, označene slovima od A do D. Svaka kuća ima ploču na kojima su redom upisani sljedeći brojevi: 8, 4, 2 i 1.

Pomoć:

Potrebno je zbrojiti brojeve ispred kuća tako da zbroj daje broj $11 .$

Postupak:

$8 + 2 + 1 = 11$ tako da je $4$ višak.

O kojim se dekadskim brojevima radi?

2

5

6

9

10

13

17

20

26

31

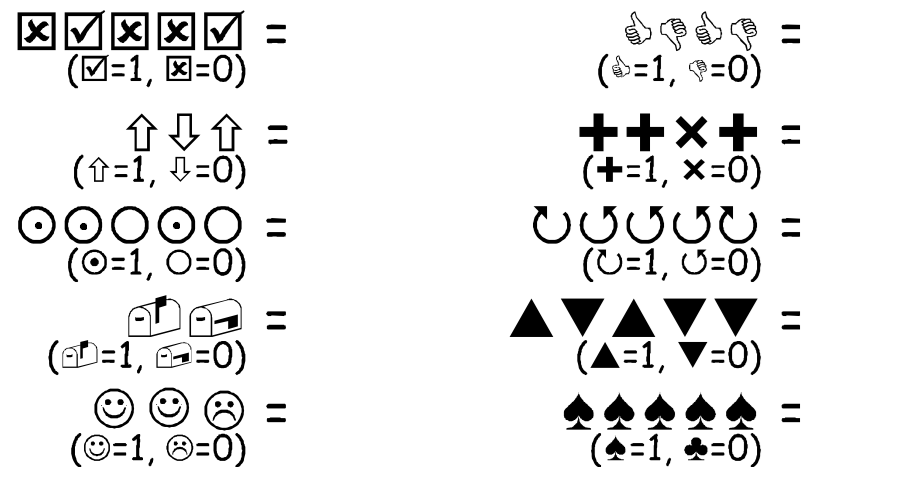
Pomoć:

Znakove prema tumačenju ispod njih napiši u obliku 0 i 1. Zatim ih pretvori u dekadski oblik.

Zadatak 3.

Broj $203.8$ iz dekadskoga sustva pretvori u sljedeća $3$ sustava (na $2$ decimale):

binarni

heksadekadski

bazom

5

Pomoć:

Pogledaj nastavnu jedinicu Brojevni sustavi.

null

Zadatak 4.

U računalu se cijeli brojevi zapisuju u 8-bitnim registrima metodom dvojnog komplementa. U dvama registrima zapisane su dekadske vrijednosti $- 73$ i $- 83 .$ U treći registar treba spremiti zbroj sadržaja ovih registara. Koji je sadržaj trećeg registra?

101100100

000001010

01100100

10011100

Pomoć:

Pogledaj nastavnu jedinicu Zbrajanje brojeva u binarnom brojevnom sustavu.

null

Zadatak 5.

U pripadne kvadratiće upiši dijelove 32-bitnog zapisa realnog broja ako se radi o standardu IEEE $754 :$

P - predznak
K - karakteristika
M - mantisa

32 bitni zapis realnog broja prema IEEE 754 standardu na kojemu pravilno treba označiti dijelove toga broja - predznak, karakteristiku i mantisu

Pomoć:

Pogledaj nastavnu jedinicu Zapis brojeva u memoriji računala

null

Koji je dekadski realni broj zapisan u gornjem registru?

Pomoć:

Pogledaj nastavnu jedinicu Zapis brojeva u memoriji računala.

null

Praktična vježba

Pokušaj miješati boje. Na ovoj adresi možeš vidjeti kako izgleda bilo koja boja u 24-bitnom zapisu. Rekli smo da se svaka boja dobije miješanjem crvene, zelene i plave (RGB). Cilj je dobiti boju s desne strane (goal colour) pomicanjem vrijednosti osnovne $3$ boje.

Nakon toga pokušaj dobiti tu istu boju u 8-bitnom zapisu. To je gotovo nemoguće. Zašto?
Jer u 24-bitnom zapisu postoji više od $16$ milijuna nijansi boja ( $2^{24}$ ), a u 8-bitnom zapisu svega $256$ boja ( $2^{8}$ ) pa je moguće da određena nijansa ne postoji u lošijoj kvaliteti.

Jednu 24-bitnu boju po izboru pretvori iz binarnog zapisa u heksadekadski. Ispred tog broja dodaj znak # te dobiveni zapis upiši u neki internetski preglednik. To je najbolja kontrola da je pretvorba bila ispravna.

Kutak za znatiželjne

U tablici su navedena približna razdoblja nastanka brojevnih sustava i naroda koji su ih koristili. Istraži koje su bile osobitosti pojedinih sustava.

Egipćani	Babilonci	Kinezi	Indijci	Grci	Rimljani	Arapi
3000 g.pr.Kr.	2000 g.pr.Kr.	oko 1400 g.pr.Kr.	1.stoljeće	2.stoljeće	6.stoljeće	6.stoljeće

Zatim pokušaj odgovoriti na nekoliko sljedećih pitanja.

$β$
$λ$
$π$
$ϕ$
$θ$