Faktorijele

Faktorijeli

Za prirodni broj $n \geq 1$ simbolom $n!$ označujemo broj (en-faktorijela) definiran s $n! = n \cdot (n - 1) \cdot \cdot \cdot 3 \cdot 2 \cdot 1 .$

Zamijetimo da je $1! = 1 .$

Dodatno definiramo $0! = 1 .$

Rezultat iz primjera mogli smo zapisati kao $8! = 40 320 .$

Pogledajmo sljedeću tablicu.

$n$	$0$	$1$	$2$	$3$	$4$	$5$	$6$
$n!$	$1$	$1$	$2$	$6$	$24$	$120$	$720$

Možemo primijetiti da faktorijele brzo rastu i da vrijedi da je $n! = n \cdot (n - 1)! .$

Zadatak 1.

Izračunajte.

a) $\frac{10!}{8!}$

b) $\frac{3!}{5!}$

a) $\frac{10!}{8!} = \frac{10 \cdot 9 \cdot 8!}{8!} = 90$

b) $\frac{3!}{5!} = \frac{3!}{5 \cdot 4 \cdot 3!} = \frac{1}{20}$

Zadatak 2.

Odredite $n$ ako je $n! = 3! \cdot 5! \cdot 7! .$

Nakon raspisivanja i grupiranja možemo izračunati $n = 10 .$

Christian Kramp – francuski matematičar koji je prvi upotrijebio zapis faktorijela koji se danas koristi. — Christian Kramp

Zanimljivost

Christian Kramp, francuski matematičar, prvi je u svojemu djelu Éléments d'Arithmétique Universelle iz 1808. godine upotrijebio zapis za faktorijele kakav danas poznajemo.

Istražite! Koliko iznosi maksimalan broj $n$ za koji možete odrediti vrijednost faktorijele s pomoću vašeg računala.

Binomni koeficijenti

Kutak za znatiželjne

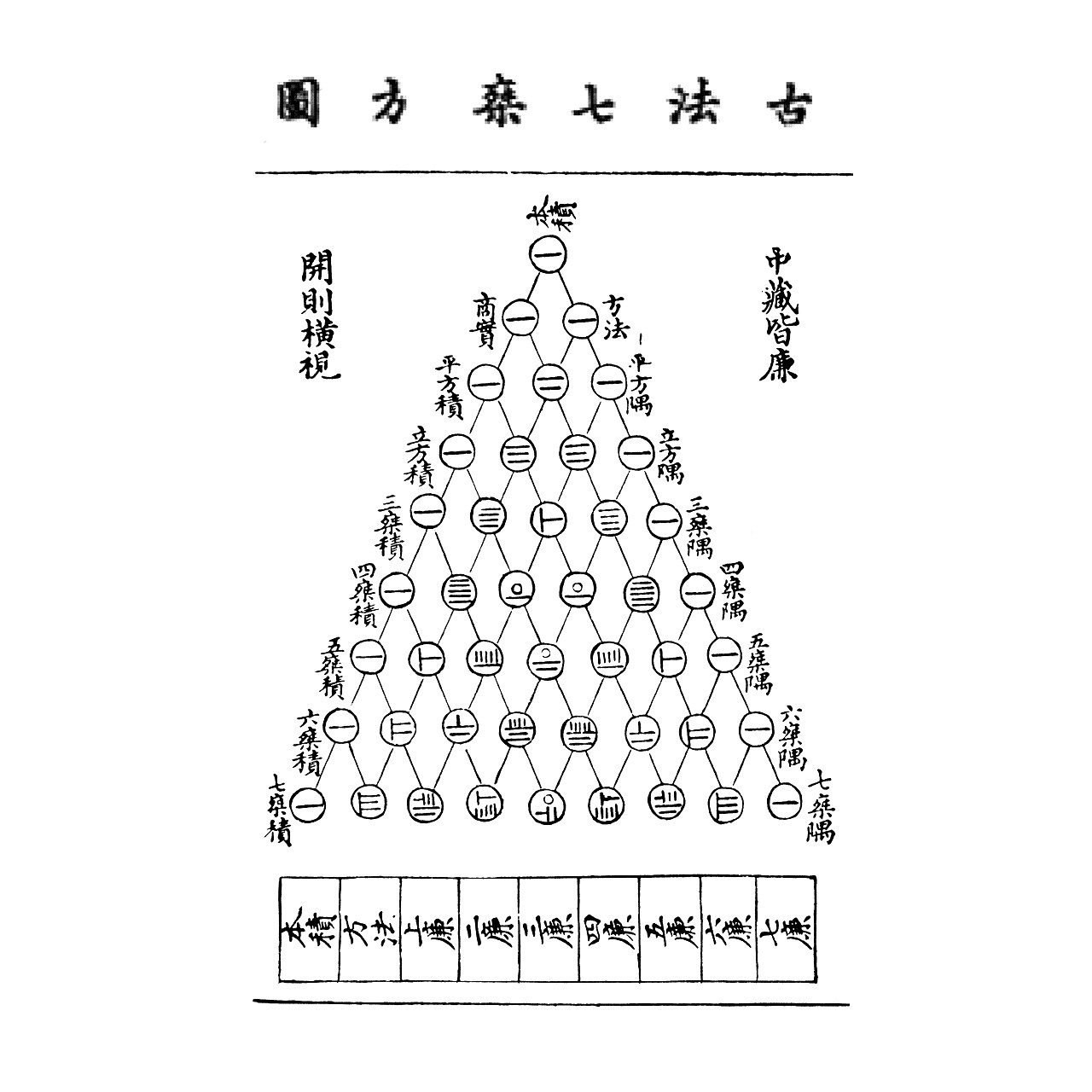
Binomni koeficijenti pozitivni su cijeli brojevi koji se pojavljuju kao koeficijenti u binomnom poučku, a upotrebljavaju se i u računanju kombinacija. Poznati su stoljećima, ali najpoznatiji su iz djela Blaisea Pascala još iz 1640. godine.

Iako je trokut poznat kao Pascalov trokut, bio je poznat u Kini već u 13. stoljeću kao Yang Huiev trokut.

Binomni koeficijenti

Za brojeve $n,$ $k \in N_{0},$ $0 \leq k \leq n,$ definiramo binomni koeficijent $(\begin{array}{l} n \\ k \end{array})$ (čitamo en povrh ka):

$(\begin{array}{l} n \\ k \end{array}) = \frac{n!}{k! \cdot (n - k)!} .$

Primjer 2.

Izračunajmo $(\begin{array}{l} 7 \\ 3 \end{array}) .$

$(\begin{array}{l} 7 \\ 3 \end{array}) = \frac{7!}{3! \cdot (7 - 3)!} = \frac{7 \cdot 6 \cdot 5 \cdot 4!}{3! \cdot 4!} = \frac{7 \cdot 6 \cdot 5}{1 \cdot 2 \cdot 3} = 7 \cdot 5 = 35 .$

Uparite binomne koeficijente i rješenja.

$(\begin{array}{l} 8 \\ 3 \end{array})$	$10$
$(\begin{array}{l} 6 \\ 2 \end{array})$	$15$
$(\begin{array}{l} 10 \\ 3 \end{array})$	$120$
$(\begin{array}{l} 5 \\ 3 \end{array})$	$56$

null

Svojstva binomnih koeficijenata

Primjer 3.

Izračunajmo redom binomne koeficijente.

$(\begin{array}{l} 1 \\ 0 \end{array}),$ $(\begin{array}{l} 1 \\ 1 \end{array}),$ $(\begin{array}{l} 2 \\ 0 \end{array}),$ $(\begin{array}{l} 2 \\ 1 \end{array}),$ $(\begin{array}{l} 2 \\ 2 \end{array}),$ $(\begin{array}{l} 3 \\ 0 \end{array}),$ $(\begin{array}{l} 3 \\ 1 \end{array}),$ $(\begin{array}{l} 3 \\ 2 \end{array}),$ $(\begin{array}{l} 3 \\ 3 \end{array}) . . .$

Primjenjujući definiciju dobit ćemo redom:

$1,$ $1,$ $1,$ $2,$ $1,$ $1,$ $3,$ $3,$ $1,$ $. . .$

Možemo zamijetiti da je:

$(\begin{array}{l} 1 \\ 0 \end{array}) = (\begin{array}{l} 1 \\ 1 \end{array}),$ te $(\begin{array}{l} 2 \\ 0 \end{array}) = (\begin{array}{l} 2 \\ 2 \end{array})$ i $(\begin{array}{l} 3 \\ 0 \end{array}) = (\begin{array}{l} 3 \\ 3 \end{array}) .$

Što možemo zaključiti?

(\begin{array}{l} n \\ 0 \end{array}) =

.

null

(\begin{array}{l} n \\ n \end{array}) =

.

null

Složimo sada binomne koeficijente u redove prema vrijednosti broja $n .$

$n = 0$	$(\begin{array}{l} 0 \\ 0 \end{array}) = 1$
$n = 1$	$(\begin{array}{l} 1 \\ 0 \end{array}) = 1$ $(\begin{array}{l} 1 \\ 1 \end{array}) = 1$
$n = 2$	$(\begin{array}{l} 2 \\ 0 \end{array}) = 1$ $(\begin{array}{l} 2 \\ 1 \end{array}) = 2$ $(\begin{array}{l} 2 \\ 2 \end{array}) = 1$
$n = 3$	$(\begin{array}{l} 3 \\ 0 \end{array}) = 1$ $(\begin{array}{l} 3 \\ 1 \end{array}) = 3$ $(\begin{array}{l} 3 \\ 2 \end{array}) = 3$ $(\begin{array}{l} 3 \\ 3 \end{array}) = 1$
$n = 4$	$(\begin{array}{l} 4 \\ 0 \end{array}) = 1$ $(\begin{array}{l} 4 \\ 1 \end{array}) = 4$ $(\begin{array}{l} 4 \\ 2 \end{array}) = 6$ $(\begin{array}{l} 4 \\ 3 \end{array}) = 4$ $(\begin{array}{l} 4 \\ 4 \end{array}) = 1$
$n = 5$	$(\begin{array}{l} 5 \\ 0 \end{array}) = 1$ $(\begin{array}{l} 5 \\ 1 \end{array}) = 5$ $(\begin{array}{l} 5 \\ 2 \end{array}) = 10$ $(\begin{array}{l} 5 \\ 3 \end{array}) = 10$ $(\begin{array}{l} 5 \\ 4 \end{array}) = 5$ $(\begin{array}{l} 5 \\ 5 \end{array}) = 1$

Struktura koju smo dijelom složili naziva se Pascalov trokut.

Binomni koeficijenti sljedećeg reda mogu se dobiti zbrajanjem određenih članova prethodnog reda.

Kako?

Primjer 4.

Za $n = 4$ i $n = 5$ zamijetimo da vrijedi:

$(\begin{array}{l} 4 \\ 2 \end{array}) + (\begin{array}{l} 4 \\ 3 \end{array}) = (\begin{array}{l} 5 \\ 3 \end{array})$

ili

$(\begin{array}{l} 4 \\ 1 \end{array}) + (\begin{array}{l} 4 \\ 2 \end{array}) = (\begin{array}{l} 5 \\ 2 \end{array}) .$

Svojstvo Pascalovog trokuta

Za binomne koeficijente vrijedi sljedeće svojstvo:

$(\begin{array}{l} n \\ k \end{array}) + (\begin{array}{l} n \\ k + 1 \end{array}) = (\begin{array}{l} n + 1 \\ k + 1 \end{array}),$ $k = 0, 1, . . . n - 1;$

Pogledajte dokaz svojstva u sljedećem videu.

Primjer 5.

Odredimo:

a) $(\begin{array}{l} 6 \\ 1 \end{array})$ i $(\begin{array}{l} 6 \\ 5 \end{array}) .$

Prema definiciji imamo:

$(\begin{array}{l} 6 \\ 1 \end{array}) = \frac{6!}{1! \cdot 5!} = \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}{1 \cdot 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} = 6$ i $(\begin{array}{l} 6 \\ 5 \end{array}) = \frac{6!}{5! \cdot 1!} = 6 .$

b) $(\begin{array}{l} n \\ 1 \end{array})$ i $(\begin{array}{l} n \\ n - 1 \end{array})$

Prema definiciji imamo:

$(\begin{array}{l} n \\ 1 \end{array}) = \frac{n!}{1! \cdot (n - 1)!}$

$(\begin{array}{l} n \\ n - 1 \end{array}) = \frac{n!}{(n - 1)! \cdot (n - n + 1)!} = \frac{n!}{1! \cdot (n - 1)!} .$

Svojstvo simetrije

Za binomne koeficijente vrijedi svojstvo simetrije:

$(\begin{array}{l} n \\ k \end{array}) = (\begin{array}{l} n \\ n - k \end{array}) .$

S pomoću svojstva simetrije spojite parove.

$(\begin{array}{l} 14 \\ 5 \end{array})$	$(\begin{array}{l} 7 \\ 3 \end{array})$
$(\begin{array}{l} 7 \\ 4 \end{array})$	$(\begin{array}{l} 7 \\ 2 \end{array})$
$(\begin{array}{l} 7 \\ 5 \end{array})$	$(\begin{array}{l} 14 \\ 9 \end{array})$
$(\begin{array}{l} 14 \\ 11 \end{array})$	$(\begin{array}{l} 14 \\ 3 \end{array})$

null

...i na kraju

Za kraj istražite malo drukčiji Pascalov trokut i riješite jedan složeniji zadatak.

Pokušajte sastaviti aritmetički Pascalov trokut.

Zamjećujete li razliku u odnosu prema trokutu koji smo već upoznali?

Povećaj interaktivni prikaz

Zadatak 3.

Odredite pozitivan broj n za koji vrijedi:

$(\begin{array}{l} n + 2 \\ 11 \end{array}) = 109 \cdot (\begin{array}{l} n \\ 9 \end{array}) .$

Nakon raspisivanja imamo jednadžbu:

$(n + 2) (n + 1) = 110 \cdot 109 .$

Rješenje je $n = 108 .$

Procijenite svoje znanje

Povežite parove.

$2! \cdot 3!$	$12$
$3! \cdot 4!$	$144$
$5! \cdot 3!$	$720$

null

Izračunajte $\frac{10!}{5!} .$

30 240

725 760

5 443 200

null

$(\begin{array}{l} 10 \\ 3 \end{array}) = 30$

Da

Ne

null

Odaberite sve izraze iste vrijednosti kao $(\begin{array}{l} 17 \\ 11 \end{array}) .$

2 376

(\begin{array}{l} 17 \\ 6 \end{array})

(\begin{array}{l} 16 \\ 10 \end{array}) + (\begin{array}{l} 16 \\ 11 \end{array})

(\begin{array}{l} 11 \\ 17 \end{array})

null

10.1 Binomni koeficijenti

Na početku...

Primjer 1.

Faktorijele

Faktorijeli

Zadatak 1.

Zadatak 2.

Zanimljivost

Binomni koeficijenti

Kutak za znatiželjne

Binomni koeficijenti

Primjer 2.

Svojstva binomnih koeficijenata

Primjer 3.

Primjer 4.

Svojstvo Pascalovog trokuta

Primjer 5.

Svojstvo simetrije

...i na kraju

Zadatak 3.

Procijenite svoje znanje

MOJE ZNANJE

Uspješno ste usvojili sve odgojno-obrazovne ishode:

Potrudite se još malo kako biste bolje usvojili sljedeće odgojno-obrazovne ishode:

Trebali biste ponovno proći sljedeće jedinice: