

Teorija igara je matematička disciplina koja se razvila sredinom 20. stoljeća. Bavi se situacijama konflikta između dvaju ili više sudionika. Cilj je odrediti ponašanje sudionika koje je za njih najpovoljnije uz strogo određena pravila kao što su u društvenim igrama poput Šaha, Čovječe ne ljuti se, Mlina, Binga, Jamba, Monopola, Pokera, Remija, Crnog Petra i sl.

U igri Bingo svaki igrač ima listić s
polja na kojem je nasumično smješteno 15 različitih brojeva između
i
Izvlače se brojevi i čiji svi brojevi budu prvi izvučeni, pobjednik je. Ako su istodobno popunjeni listići, pobjednik je onaj čiji je zbroj svih brojeva na listiću veći. Dobitnici su i oni koji prvi popune jedan red na kojemu je na
polja smješteno nasumično
brojeva, odnosno dva reda listića (
izvučenih brojeva).
Primjer 1.
Na koliko je načina moguće popuniti jedan red u igri Bingo?
U prvom su polju moguće sve znamenke od
do
ili polje može ostati prazno; od drugog do osmog polja moguće je imati jedan od
brojeva (npr. u drugom polju od
do
) ili prazno polje. U zadnjem je polju moguće imati broj između
i
ili prazno polje.
Prema načelu umnoška, ukupan broj kombinacija za popunjavanje jednog reda je:
Više od dvije milijarde pokušaja za samo jedan red. Razmislite, isplati li se ulagati u takve igre?
Nakon što ste se upoznali s osnovama igre Bingo, riješite sljedeće zadatke.
Izradi vježbu
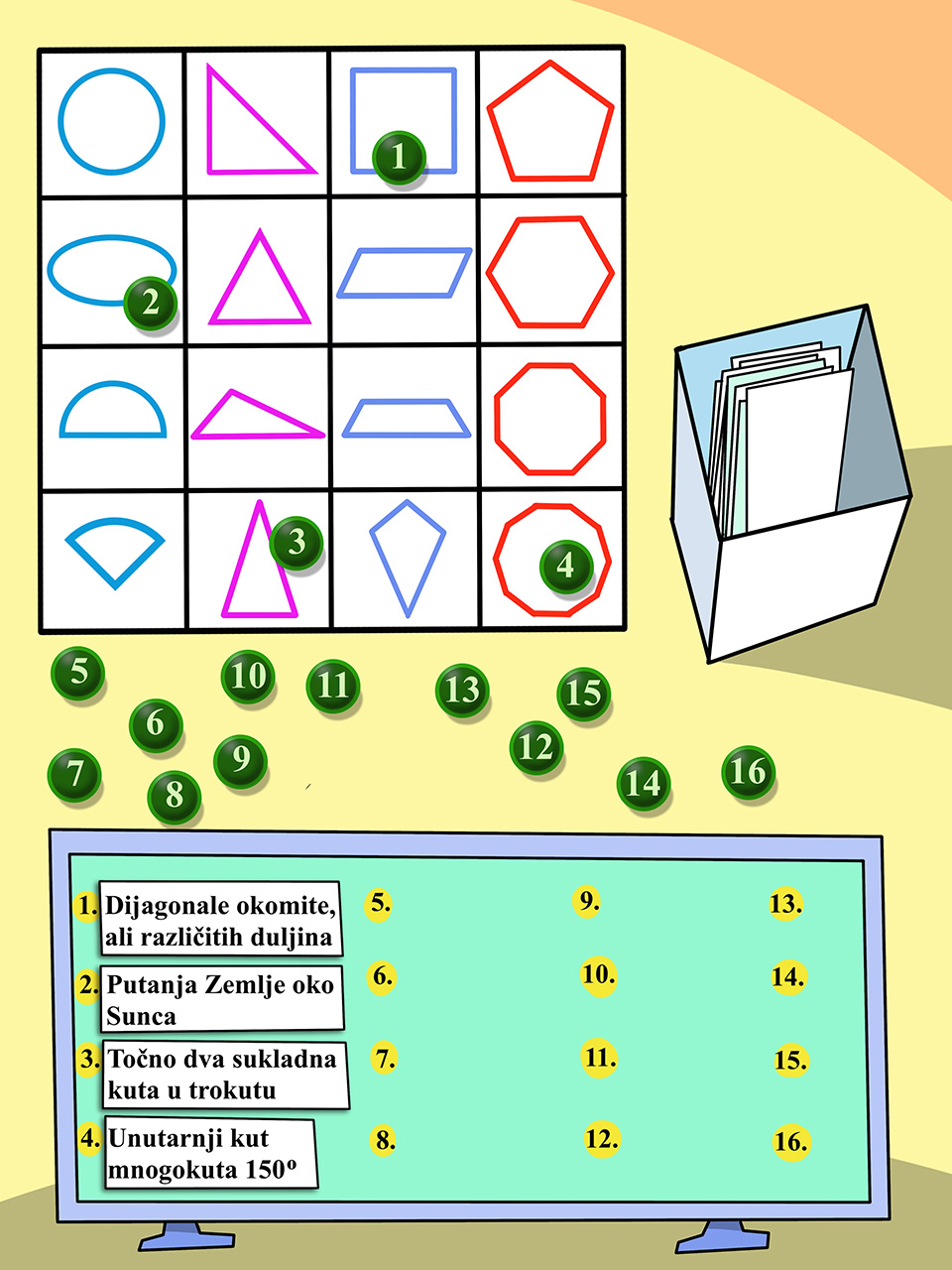
Osmislite svoj matematički bingo. Na svakoj ploči nacrtajte nekoliko geometrijskih likova. Za svaki lik može se napisati definicija, neko pravilo ili formula koja upućuje na taj lik. Svaki igrač sakrije svoju tablicu i pri izvlačenju pojma, ako se prepozna lik, pokrije se s onim rednim brojem pod kojim je taj pojam izvučen. Pobjednik je onaj koji je prepoznao najviše pojmova. Za pogrešno pogođeni pojam bodovi se oduzimaju. Igru prilagodite temi, gradivu, ili možda nekim zanimljivostima koje su vam trenutačno aktualne.

Jedna od popularnijih igara s kartama je Remi. Igra se s jednim ili dva špila od
karte s džokerom ili bez njega. U igri može sudjelovati od
do
igrača. U prvom krugu se svakom igraču podijeli određeni broj karata. Tko se prvi oslobodi svih karata, pobjednik je toga kruga. Ostalima se zbrajaju bodovi karata preostalih u rukama. Karata se rješavamo tako da skupimo najmanje tri jednake karte ili barem tri u nizu iste boje (tzv. tris) i slažemo ih na stol.
Nakon što ste pročitali osnovna pravila igre Remi odgovorite na slljedeća pitanja.
Primjer 2.
Koliko je kombinacija moguće dobiti jednim bacanjem pet kockica s brojevima od do
Redoslijed elemenata važan je u istodobnom bacanju pet kockica?
Brojevi (elementi skupa) mogu se ponavljati?
O kojem je tipu zadatka ovdje riječ?
Koliko je mogućih kombinacija brojeva na pet istodobno bačenih kockica?
Na koliko je načina moguće dobiti jamb (na svim kockicama isti broj) ako su u prvom bacanju pala tri ista broja, u drugome još jedan te u trećemu bacanju peti isti broj? Kada dobijemo na kockici broj koji želimo, tu kockicu u sljedećem krugu više ne bacamo.
U prvom se bacanju tri broja razlikuju, a preostala dva podudaraju se s jednim od prva tri. Jedan broj se tri puta može ponoviti na načina, drugi i treći broj trebaju biti isti. Vrijednost četvrte i pete kockice (mogu biti i jednaki brojevi) dobijemo na različitih načina: Broj mogućih načina na kojima se od pet kockica pojave tri ista broja je Prema načelu umnoška, ukupan broj mogućih rezultata je načina.
U sljedećem bacanju imamo dva različita broja od koji je jedan definiran (broj iz prvog bacanja), a drugi može biti jedan od
preostalih, što je moguće dobiti na
načina pa je ukupan broj mogućih ishoda
U trećem bacanju znamo koji je broj pao za jamb. Prema načelu umnoška, broj različitih načina dobivanja jamba u tri bacanja po pet kockica jest
Ono što je nama zanimljivije u takvim igrama na sreću jest vjerojatnost dobitka. Zavirimo malo u to područje matematike.
Teorija vjerojatnosti je široj javnosti najzanimljivija grana matematike najviše zbog primjene u igrama na sreću. Prvi dokazi početaka igre na sreću potječu još iz razdoblja oko 3500 g. pr. Krista. To su bile posebne kosti ovčjih papaka koje su imale dvije zaobljene plohe i četiri podjednaka kvadrata (astragaloi). Ljudi su se kladili na četiri moguća ishoda, na koju će od četiri plohe pasti kockica.
Više o povijesti kombinatorne teorije vjerojatnosti možete pročitati u diplomskom radu Helene Dravec: Počeci razvoja kombinatorne teorije vjerojatnosti.
Prisjetimo se klasične definicije vjerojatnosti za neki događaj gdje je broj povoljnih događaja, a broj svih mogućih događaja promatranog skupa elementarnih događaja
Primjer 3.
Izračunajmo kolika je vjerojatnost da nam s jednim bacanjem pet kockica odjedanput padnu tri ista broja. Neka je
U 1. zadatku izračunali ste na koliko različitih načina možemo dobiti tri ista broja na kockicama. Imamo permutacije s ponavljanjem te prema načelu umnoška izračunamo sve moguće načine dobivanja triju istih brojeva i preostalih dvaju koji se razlikuju od tih triju.
Kako računamo kardinalni broj skupa elementarnih događaja,
Koristeći se pravilima kombinatrike, izračunajte sljedeće vjerojatnosti događaja.
Za lakše određivanje formule, odnosno pravila računanja kardinalnog broja povoljnih ishoda može vam poslužiti sljedeća interakcija.
Uz pomoć prethodne interakcije riješite sljedeće zadatke.
Jeste li čuli za jedno od najpoznatijih kombinatornih pravila, pravilo pretinaca ili pravilo kutija?
U nastavku ćemo se upoznati s tim pravilom.
Pierre Gustave Lejeune Dirichlet (1805. – 1859.), njemački je matematičar francuskog podrijetla. Najveći doprinos u matematici dao je na području teorije brojeva i matematičkoj analizi. Njegov suvremenik, jedan od najvećih matematičara, Gauss, bio mu je uzor, kojeg je nakon smrti i naslijedio na Göttingenskom sveučilištu.
Jedna od varijanti formulacije Dirichletova pravila jest sa zečevima: Ako
zečeva rasporedimo bilo kako u
kaveza, onda su barem u jednom kavezu smještena barem dva zeca.
Dirichletovo pravilo
Ako predmeta bilo kako rasporedimo u kutija, onda barem jedna kutija sadržava bar dva predmeta.
Ta je tvrdnja očita kao i dokaz tvrdnje. Pogledajte sljedeću animaciju kojom se dokazuje spomenuto pravilo.
Primjer 4.
Jedan tipični primjer primjene tog pravila je s rođendanima. Podijelimo svaki mjesec na kvartale. Neka je prvi kvartal mjeseca od 1. do 7. dana; drugi kvartal je od 8. do 15., treći od 16. do 23. te od 24. do kraja je zadnji kvartal u mjesecu.
- Hoće li između pet prijatelja barem dva imati rođendan u istom kvartalu mjeseca?
- Koliko će u razredu od 25 učenika minimalno biti onih koji su rođeni u istom kvartalu mjeseca?
Pomoću Dirichletovog principa riješite još dva problema.
Riješite za kraj sljedeći problem.
Iz bubnja s brojevima
izvlačimo nasumično 6 brojeva.