Matematika 4 - Aktivnosti za samostalno učenje

Na početku...

Podsjetimo se: kompleksni broj jest broj koji ima oblik $z = a + b i,$ gdje su $a$ i $b$ realni brojevi, a $i$ imaginarna jedinica, $i^{2} = - 1 .$

Zadatak 1.

Uparite zadatak s odgovarajućim rješenjem.

$\frac{6 + 8 i}{1 + i} =$	$7 + i$
$(2 - i) (3 + 5 i) =$	$11 + 7 i$
$(- 4 + 5 i) - (1 - 2 i) =$	$- 5 + 7 i$
$(3 - 4 i) + (12 + 7 i) =$	$15 + 3 i$
${(- 5 + 2 i)}^{2} =$	$21 - 20 i$

null

Kompleksne brojeve prikazujemo u Gaussovoj ravnini.

Zadatak 2.

Koji od navedenih kompleksnih brojeva nisu prikazani točkom na slici?

$2 i$

$3 - i$

$- 1 + 3 i$

$- 2 - 3 i$

$- 5$

$2 + 3 i$

null

Računanje s kompleksnim brojevima u Gaussovoj ravnini

U prethodnim ste jedinicama istražili kako geometrijski interpretirati zbroj i razliku dvaju kompleksnih brojeva.

Zadatak 3.

ishodište i
$z_{1}$ i $z_{2}$ prikazan je
četvrtim vrhom paralelograma
zadani brojevi $z_{1}$ i $z_{2} .$
Zbroj
čija su tri vrha
dvaju kompleksnih brojeva

null

Kutak za znatiželjne

Kako interpretiramo množenje kompleksnih brojeva u Gaussovoj ravnini? Pogledajmo u interakciji.

00:00

Uočavate li vezu s množenjem kompleksnih brojeva u trigonometrijskom obliku?

$z_{1} \cdot z_{2} = r_{1} \cdot r_{2} (\cos (φ_{1} + φ_{2}) + i \sin (φ_{1} + φ_{2}))$

Moduli se pomnože, a argumenti zbroje.

...i na kraju

Korjenovanje kompleksnih brojeva

Odredimo sve kompleksne brojeve $z$ za koje je $z^{3} = 8 .$

Zapišimo jednadžbu $z^{3} - 1 = 0 .$ Faktorizacijom brzo dolazimo do jednoga realnog rješenja, $z_{1} = 2 .$

$z^{3} - 8 = (z - 2) (z^{2} + 2 z + 4) .$

Sljedeća rješenja dobijemo rješavanjem kvadratne jednadžbe $z^{2} + 2 z + 4 = 0 .$ To su $z_{2,3} = - 1 \pm \sqrt{3} i .$

Nacrtajmo ta rješenja u Gaussovoj ravnini.

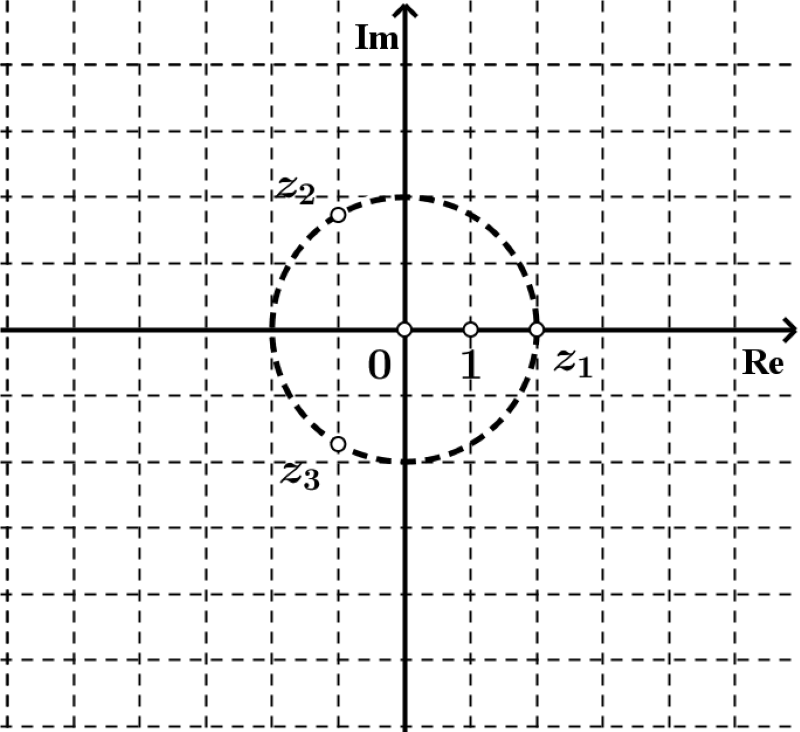
Korjenovanje kompleksnih brojeva — Gaussova ravnina

Vidimo da se sva tri rješenja nalaze na kružnici polumjera $2$ i da čine jednakostranični trokut.

U ovome smo zadatku mogli riješiti kvadratnu jednadžbu s pomoću formule. Međutim, za jednadžbe višega stupnja nam služi sljedeća formula u kojoj se koristimo trigonometrijskim zapisom kompleksnoga broja.

Svaki kompleksan broj $z = r (\cos φ + i \sin φ)$ ima točno $n$ različitih $n$ -tih korijena danih formulom:

$\sqrt[n]{r} (\cos \frac{φ + 2 k π}{n} + i \sin \frac{φ + 2 k π}{n})$ za $k = 1, 2,..., n - 1,$ $n \in N .$

Istražite formulu!

Riješite sjedeći zadatak: Odredite sve kompleksne brojeve za koje je $z^{5} = 1 .$

$z_{1} = 1$

$z_{2} = \cos \frac{2 π}{5} + i \sin \frac{2 π}{5}$

$z_{3} = \cos \frac{4 π}{5} + i \sin \frac{4 π}{5}$

$z_{4} = \cos \frac{6 π}{5} + i \sin \frac{6 π}{5}$

$z_{5} = \cos \frac{8 π}{5} + i \sin \frac{8 π}{5}$

1.6 Aktivnosti za samostalno učenje

Na početku...

Zadatak 1.

Zadatak 2.

Računanje s kompleksnim brojevima u Gaussovoj ravnini

Zadatak 3.

Kutak za znatiželjne

Jednadžbe i nejednadžbe

Zadatak 4.

...i na kraju