Matematika 4 - 4.4 Pravila deriviranja

Derivacija umnoška konstante i funkcije

Istražimo

Odredite po definiciji derivacije funkcija:

$f (x) = 5 x^{2}$

$g (x) = 7 x^{2}$

$h (x) = 2 x^{3}$

$i (x) = 6 x^{3} .$

Uočavate li pravilnost? Riješite sljedeće zadatke.

Kolekcija zadataka #1

Poredajte korake računanja.

$\lim_{Δ x \to 0}$ $\frac{f (x + Δ x) - f (x)}{Δ x}$ $=$
$10 x$
$\lim_{Δ x \to 0} (10 x + 5 Δ x) =$
${(5 x^{2})}^{'} = 10 x$
$\lim_{Δ x \to 0} \frac{Δ x (10 x + 5 Δ x)}{Δ x} =$
$\lim_{Δ x \to 0}$ $\frac{5 x^{2} + 10 x \cdot Δ x + 5 {(Δ x)}^{2} - 5 x^{2}}{Δ x}$ $=$
$\lim_{Δ x \to 0} \frac{5 {(x + Δ x)}^{2} - 5 x^{2}}{Δ x} =$

null

Uparite funkciju i njezinu derivaciju.

${(7 x^{2})}^{'} =$	$18 x^{2}$
${(5 x^{2})}^{'} =$	$10 x$
${(6 x^{3})}^{'} =$	$14 x$
${(2 x^{3})}^{'} =$	$6 x^{2}$

null

${(5 x^{2})}^{'} =$

${(x^{2})}^{'} =$

pa je

${(5 x^{2})}^{'} =$

${(x^{2})}^{'} .$

$2 x$

$5$

$10 x$

null

${(2 x^{3})}^{'} =$

${(x^{3})}^{'} =$

pa je

${(2 x^{3})}^{'} =$

${(x^{3})}^{'} .$

$6 x^{2}$

$3 x^{2}$

$2$

null

${(7 x^{2})}^{'} =$

${(x^{2})}^{'} .$

${(6 x^{3})}^{'} =$

${(x^{3})}^{'} .$

null

Uočena pravilnost vrijedi za svaku derivabilnu funkciju $f$ i konstantu $c .$

${(c f)}^{'} =$

$f^{'} .$

null

Za svaku derivabilnu funkciju $f$ i realni broj $c$ vrijedi ${(c f)}^{'} = c f^{'} .$

Dokažimo ovu tvrdnju.

$\begin{aligned} {(c f (x))}^{'} & = \lim_{Δ x \to 0} \frac{c f (x + Δ x) - c f (x)}{Δ x} = \lim_{Δ x \to 0} c \frac{f (x + Δ x) - f (x)}{Δ x} = \\ = c \lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} = c f^{'} (x) \end{aligned}$

Derivacija zbroja funkcija

Istražimo

Istražite kako možemo računati derivaciju zbroja funkcija. Izračunajte po definiciji derivaciju funkcije $h (x) = x + x^{2} .$ Što možete pretpostaviti? Odaberite još neke primjere pa provjerite pretpostavku.

$\begin{array}{ll} {(x + x^{2})}^{'} & = \lim_{Δ x \to 0} \frac{(x + Δ x) + {(x + Δ x)}^{2} - x - x^{2}}{Δ x} = \\ = \lim_{Δ x \to 0} \frac{(x + Δ x) - x}{Δ x} + \lim_{Δ x \to 0} \frac{{(x + Δ x)}^{2} - x^{2}}{Δ x} = {(x)}^{'} + {(x^{2})}^{'} \end{array}$

Uočavamo da je derivacija zbroja funkcija jednaka zbroju njihovih derivacija.

Uočeno pravilo vrijedi općenito.

Derivacija zbroja

Za derivabilne funkcije $f$ i $g$ vrijedi ${(f + g)}^{'} = f^{'} + g^{'} .$

Kutak za znatiželjne

Dokažite pravilo za derivaciju zbroja.

$\begin{array}{ll} {(f + g)}^{'} (x) & = \lim_{Δ x \to 0} \frac{(f + g) (x + Δ x) - (f + g) (x)}{Δ x} = \\ = \lim_{Δ x \to 0} \frac{f (x + Δ x) + g (x + Δ x) - f (x) - g (x)}{Δ x} = \\ = \lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} + \lim_{Δ x \to 0} \frac{g (x + Δ x) - g (x)}{Δ x} = \\ = f^{'} (x) + g^{'} (x) \end{array}$

Zadatak 1.

Odredite derivaciju funkcije primjenjujući pravila i derivaciju potencije.

${(4 x^{5} - 2 x^{7})}^{'}$
${(3 x^{4} + 6 x^{8})}^{'}$

$\begin{array}{ll} {(4 x^{5} - 2 x^{7})}^{'} & = {(4 x^{5})}^{'} + {(- 2 x^{7})}^{'} = 4 {(x^{5})}^{'} - 2 {(x^{7})}^{'} = \\ = 4 \cdot 5 x^{4} - 2 \cdot 7 x^{6} = 20 x^{4} - 14 x^{6} \end{array}$
$\begin{array}{ll} {(3 x^{4} + 6 x^{8})}^{'} & = {(3 x^{4})}^{'} + {(6 x^{8})}^{'} = 3 {(x^{4})}^{'} + 6 {(x^{8})}^{'} = \\ = 3 \cdot 4 x^{3} + 6 \cdot 8 x^{7} = 12 x^{3} + 48 x^{7} \end{array}$

Derivacija umnoška

Istražimo

Istražite je li derivacija umnoška jednaka umnošku derivacija. Izračunajte:

${(x^{4} \cdot x^{7})}^{'} = {(x^{11})}^{'} =$

${(x^{4})}^{'} =$

${(x^{7})}^{'} =$

${(x^{4})}^{'} \cdot {(x^{7})}^{'} =$

Što možete zaključiti?

${(x^{4} \cdot x^{7})}^{'} = {(x^{11})}^{'} = 11 x^{10}$

${(x^{4})}^{'} = 4 x^{3}$

${(x^{7})}^{'} = 7 x^{6}$

${(x^{4})}^{'} \cdot {(x^{7})}^{'} = 4 x^{3} \cdot 7 x^{6} = 28 x^{9}$

Vidimo da derivacija umnoška nije jednaka umnošku derivacija.

Istražimo

Vidjeli smo da derivacija umnoška nije jednaka umnošku derivacija. Pogledajte kako možemo dobiti derivaciju umnoška.

Kolekcija zadataka #2

${(x^{4} \cdot x^{7})}^{'} = {(x^{11})}^{'} = 11 x^{10} = 4 x^{3} \cdot$

$+$

$\cdot 7 x^{6}$

$x^{4}$

$x^{7}$

null

${(x^{6} \cdot x^{2})}^{'} = {(x^{8})}^{'} = 8 x^{7} = 6 x^{5} \cdot$

$+$

$\cdot 2 x$

$x^{6}$

$x^{2}$

null

Uočite pravilnost u prethodnim primjerima. Što možemo pretpostaviti? Riješite zadatak.

${(f \cdot g)}^{'} = f^{'} \cdot$

$+$

$\cdot g^{'}$

$g$

$f$

null

Primjer 1.

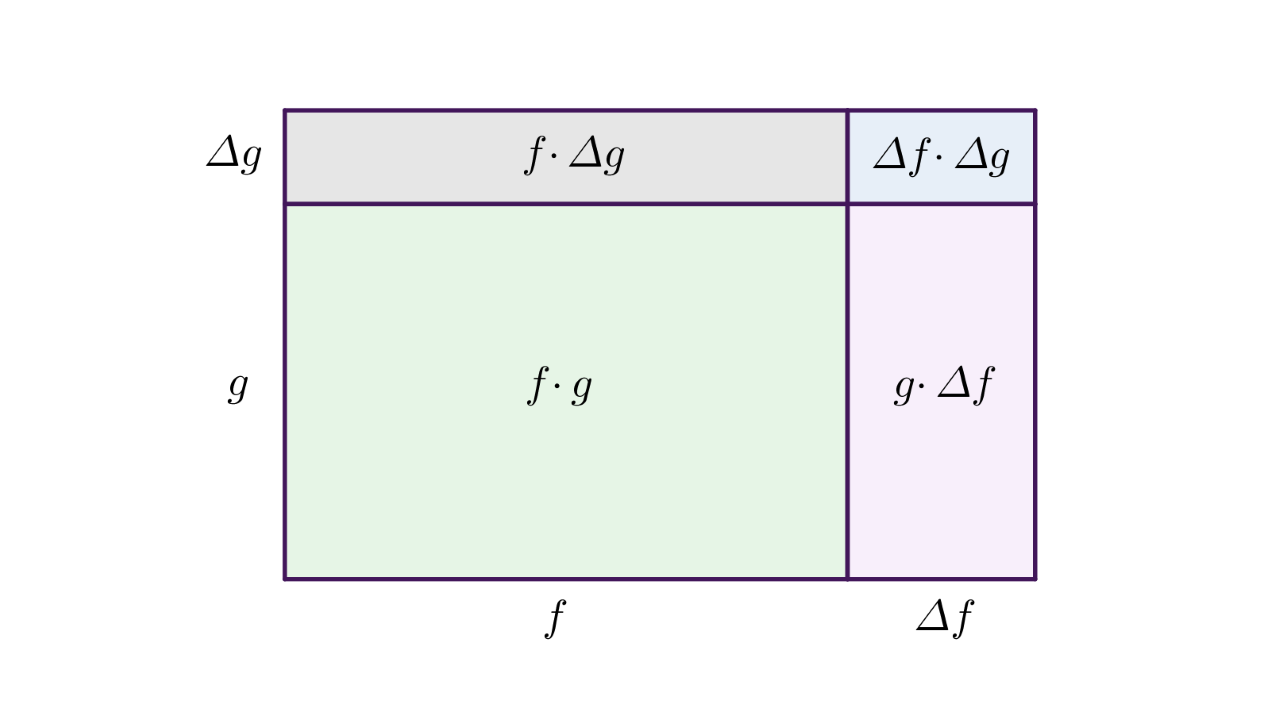
Pokažimo da uočena pravilnost vrijedi za pozitivne derivabilne funkcije $f$ i $g .$ Pogledajte na slici dolje grafički prikaz. Zapišimo $Δ (f g) :$

$\begin{array}{l} Δ (f g) = (f + Δ f) (g + Δ g) - f g = f Δ g + g Δ f + Δ f Δ g \end{array} .$

Podijelimo dobiveni izraz s $Δ x .$

$\begin{array}{l} \frac{Δ (f g)}{Δ x} = f \frac{Δ g}{Δ x} + g \frac{Δ f}{Δ x} + \frac{Δ f}{Δ x} Δ g \end{array}$ pa je $\begin{array}{l} \lim_{Δ x \to 0} \frac{Δ (f g)}{Δ x} = f \lim_{Δ x \to 0} \frac{Δ g}{Δ x} + g \lim_{Δ x \to 0} \frac{Δ f}{Δ x} + \lim_{Δ x \to 0} \frac{Δ f}{Δ x} \lim_{Δ x \to 0} Δ g \end{array} .$

${(f g)}^{'} = f g^{'} + g f^{'} + f^{'} \cdot 0 = f g^{'} + g f^{'} .$

Dobivena formula vrijedi za sve derivabilne funkcije $f$ i $g .$

Igra u kojoj se treba upariti funkcija i njezina derivacija. — Definicija derivacije

Derivacija umnoška

Za derivabilne funkcije $f$ i $g$ vrijedi ${(f \cdot g)}^{'} = f^{'} g + f g^{'} .$

Zadatak 2.

Odredite derivaciju funkcije $h (x) = (2 x^{3} - 3 x) (5 x^{2} + x) .$

$\begin{array}{ll} h^{'} (x) & = {(2 x^{3} - 3 x)}^{'} (5 x^{2} + x) + (2 x^{3} - 3 x) {(5 x^{2} + x)}^{'} = \\ = (6 x^{2} - 3) (5 x^{2} + x) + (2 x^{3} - 3 x) (10 x + 1) = \\ = 30 x^{4} + 6 x^{3} - 15 x^{2} - 3 x + 20 x^{4} + 2 x^{3} - 30 x^{2} - 3 x = \\ = 50 x^{4} + 8 x^{3} - 45 x^{2} - 6 x \end{array} .$

Derivaciju smo mogli odrediti i na drugi način. Pomnožite najprije zagrade pa zatim derivirajte.

Derivacija kvocijenta

Primjer 2.

Odredimo derivaciju kvocijenta. Neka su $f$ i $g$ derivabilne funkcije, $g \neq 0 .$ Označimo $\frac{f}{g} = t .$ Tada je $f = g t$ pa je $f^{'} = g^{'} t + g t^{'} .$

Izrazimo $t^{'} :$

$\begin{array}{ll} {(\frac{f}{g})}^{'} = t^{'} = \frac{f^{'}}{g} - \frac{g^{'} t}{g} = \frac{f^{'}}{g} - \frac{g^{'} f}{g^{2}} = \frac{f^{'} g - g^{'} f}{g^{2}} \end{array} .$

Derivacija kvocijenta

Za derivabilne funkcije $f$ i $g,$ $g \neq 0$ vrijedi ${(\frac{f}{g})}^{'} = \frac{f^{'} g - f g^{'}}{g^{2}} .$

Primjer 3.

Odredimo derivaciju funkcije $h (x) = \frac{x^{3} - x}{x + 1} .$ Pogledajte primjenu formule za derivaciju kvocijenta u videu.

00:00

Zadatak 3.

Odredite derivaciju funkcije $h (x) = \frac{x^{2} + x + 1}{x^{2} + 1} .$

$\begin{array}{ll} h^{'} (x) & = \frac{{(x^{2} + x + 1)}^{'} (x^{2} + 1) - (x^{2} + x + 1) {(x^{2} + 1)}^{'}}{{(x^{2} + 1)}^{2}} = \\ = \frac{(2 x + 1) (x^{2} + 1) - (x^{2} + x + 1) \cdot 2 x}{{(x^{2} + 1)}^{2}} = \\ = \frac{2 x^{3} + x^{2} + 2 x + 1 - 2 x^{3} - 2 x^{2} - 2 x}{{(x^{2} + 1)}^{2}} = \\ = \frac{- x^{2} + 1}{{(x^{2} + 1)}^{2}} \end{array} .$

Riješite zadatke s derivacijama.

Kolekcija zadataka #3

${(2 x^{3} - \frac{3}{x})}^{'} =$

$6 x^{2} - 3$

$6 x^{2} - \frac{3}{x^{2}}$

$6 x^{2} + \frac{3}{x^{2}}$

$6 x + \frac{3}{x^{2}}$

null

Postupak:

$\begin{array}{l} {(2 x^{3} - \frac{3}{x})}^{'} = 2 {(x^{3})}^{'} - 3 {(x^{- 1})}^{'} = 2 \cdot 3 x^{2} - 3 \cdot (- 1) x^{- 2} = 6 x^{2} + \frac{3}{x^{2}} \end{array}$

Uparite pravilo pridruživanja i derivaciju funkcije.

$f (x) = \frac{3 x^{2}}{2 x + 1}$	$f^{'} (x) = \frac{6 x}{{(x^{2} + 1)}^{2}}$
$f (x) = \frac{3 x - 1}{2 x + 1}$	$f^{'} (x) = \frac{3 (1 - x^{2})}{{(x^{2} + 1)}^{2}}$
$f (x) = \frac{3 x}{x^{2} + 1}$	$f^{'} (x) = \frac{6 x (x + 1)}{{(2 x + 1)}^{2}}$
$f (x) = \frac{3 x^{2}}{x^{2} + 1}$	$f^{'} (x) = \frac{5}{{(2 x + 1)}^{2}}$

null

${((2 x - \sqrt{x}) (2 x + \sqrt{x}))}^{'} = x (4 x - 1)$

null

Postupak:

${((2 x - \sqrt{x}) (2 x + \sqrt{x}))}^{'} = {(4 x^{2} - x)}^{'} = 8 x - 1$

Zadatak 4.

Odredite derivacije primjenjujući pravila deriviranja. Za unos potencija i razlomaka koristite tipke ^ i / na tastaturi.

4.4 Pravila deriviranja

Na početku...

Derivacija umnoška konstante i funkcije

Istražimo

Kolekcija zadataka #1

Derivacija zbroja funkcija

Istražimo

Derivacija zbroja

Kutak za znatiželjne

Zadatak 1.

Derivacija umnoška

Istražimo

Istražimo

Kolekcija zadataka #2

Primjer 1.

Derivacija umnoška

Zadatak 2.

Derivacija kvocijenta

Primjer 2.

Derivacija kvocijenta

Primjer 3.

Zadatak 3.

Kolekcija zadataka #3

Zadatak 4.

...i na kraju